Racah W-coefficient
Racah's W-coefficients were introduced by Giulio Racah in 1942.[1] These coefficients have a purely mathematical definition. In physics they are used in calculations involving the quantum mechanical description of angular momentum, for example in atomic theory.
The coefficients appear when there are three sources of angular momentum in the problem. For example, consider an atom with one electron in an s orbital and one electron in a p orbital. Each electron has electron spin angular momentum and in addition the p orbital has orbital angular momentum (an s orbital has zero orbital angular momentum). The atom may be described by LS coupling or by jj coupling as explained in the article on angular momentum coupling. The transformation between the wave functions that correspond to these two couplings involves a Racah W-coefficient.
Apart from a phase factor, Racah's W-coefficients are equal to Wigner's 6-j symbols, so any equation involving Racah's W-coefficients may be rewritten using 6-j symbols. This is often advantageous because the symmetry properties of 6-j symbols are easier to remember.
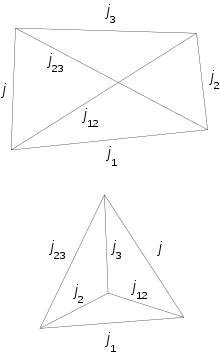
Racah coefficients are related to recoupling coefficients by
Recoupling coefficients are elements of a unitary transformation and their definition is given in the next section. Racah coefficients have more convenient symmetry properties than the recoupling coefficients (but less convenient than the 6-j symbols).[2]
Recoupling coefficients
Coupling of two angular momenta and is the construction of simultaneous eigenfunctions of and , where , as explained in the article on Clebsch–Gordan coefficients. The result is
where and .
Coupling of three angular momenta , , and , may be done by first coupling and to and next coupling and to total angular momentum :
Alternatively, one may first couple and to and next couple and to :
Both coupling schemes result in complete orthonormal bases for the dimensional space spanned by
Hence, the two total angular momentum bases are related by a unitary transformation. The matrix elements of this unitary transformation are given by a scalar product and are known as recoupling coefficients. The coefficients are independent of and so we have
The independence of follows readily by writing this equation for and applying the lowering operator to both sides of the equation.
Algebra
Let
be the usual triangular factor, then the Racah coefficient is a product of four of these by a sum over factorials,
where
and
The sum over is finite over the range[3]
Relation to Wigner's 6-j symbol
Racah's W-coefficients are related to Wigner's 6-j symbols, which have even more convenient symmetry properties
Cf.[4] or
Notes
- Racah, G. (1942). "Theory of Complex Spectra II". Physical Review. 62 (9–10): 438–462. Bibcode:1942PhRv...62..438R. doi:10.1103/PhysRev.62.438.
- Rose, M. E. (1957). Elementary theory of angular momentum (Dover).
- Cowan, R D (1981). The theory of atomic structure and spectra (Univ of California Press), p. 148.
- Brink, D M & Satchler, G R (1968). Angular Momentum (Oxford University Press) 3 ed., p. 142. online
Further reading
- Edmonds, A. R. (1957). Angular Momentum in Quantum Mechanics. Princeton, New Jersey: Princeton University Press. ISBN 0-691-07912-9.
- Condon, Edward U.; Shortley, G. H. (1970). "Chapter 3". The Theory of Atomic Spectra. Cambridge: Cambridge University Press. ISBN 0-521-09209-4.
- Messiah, Albert (1981). Quantum Mechanics (Volume II) (12th ed.). New York: North Holland Publishing. ISBN 0-7204-0045-7.
- Sato, Masachiyo (1955). "General formula of the Racah coefficient". Progress of Theoretical Physics. 13 (4): 405–414. Bibcode:1955PThPh..13..405S. doi:10.1143/PTP.13.405.
- Brink, D. M.; Satchler, G. R. (1993). "Chapter 2". Angular Momentum (3rd ed.). Oxford: Clarendon Press. ISBN 0-19-851759-9.
- Zare, Richard N. (1988). "Chapter 2". Angular Momentum. New York: John Wiley. ISBN 0-471-85892-7.
- Biedenharn, L. C.; Louck, J. D. (1981). Angular Momentum in Quantum Physics. Reading, Massachusetts: Addison-Wesley. ISBN 0-201-13507-8.
External links
- "Racah-Wigner coefficients", Encyclopedia of Mathematics, EMS Press, 2001 [1994]