Radical axis
In Euclidean geometry, the radical axis of two non-concentric circles is the set of points whose power with respect to the circles are equal. For this reason the radical axis is also called the power line or power bisector of the two circles. In detail:
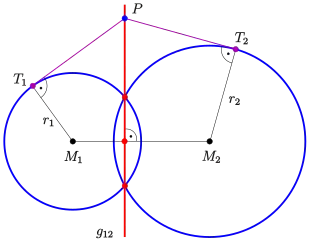
For two circles c1, c2 with centers M1, M2 and radii r1, r2 the powers of a point P with respect to the circles are
Point P belongs to the radical axis, if
If the circles have two points in common, the radical axis is the common secant line of the circles.
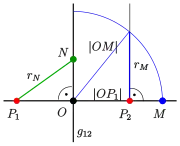
If point P is outside the circles, P has equal tangential distance to both the circles.
If the radii are equal, the radical axis is the line segment bisector of M1, M2.
In any case the radical axis is a line perpendicular to
- On notations
The notation radical axis was used by the French mathematician M. Chasles as axe radical. [1]
J.V. Poncelet used chorde ideale. [2]
J. Plücker introduced the term Chordale.[3]
J. Steiner called the radical axis line of equal powers (German: Linie der gleichen Potenzen) which led to power line (Potenzgerade).[4]
Properties
Geometric shape and its position
Let be the position vectors of the points . Then the defining equation of the radical line can be written as:
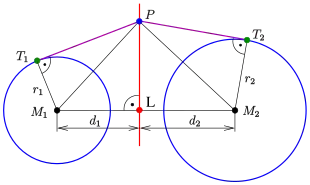
From the right equation one gets
- The pointset of the radical axis is indeed a line and is perpendicular to the line through the circle centers.
( is a normal vector to the radical axis !)
Dividing the equation by , one gets the Hessian normal form. Inserting the position vectors of the centers yields the distances of the centers to the radical axis:
- ,
- with .
( may be negative if is not between .)
If the circles are intersecting at two points, the radical line runs through the common points. If they only touch each other, the radical line is the common tangent line.
Special positions
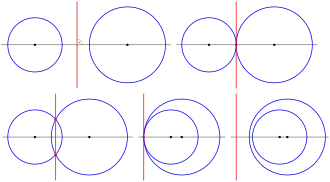
- The radical axis of two intersecting circles is their common secant line.
- The radical axis of two touching circles is their common tangent.
- The radical axis of two non intersecting circles is the common secant of two convenient equipower circles (see below).
Orthogonal circles
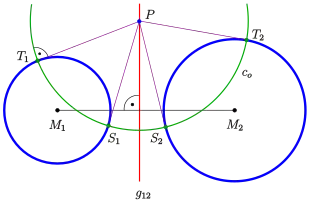
- For a point outside a circle and the two tangent points the equation holds and lie on the circle with center and radius . Circle intersects orthogonal. Hence:
- If is a point of the radical axis, then the four points lie on circle , which intersects the given circles orthogonally.
- The radical axis consists of all centers of circles, which intersect the given circles orthogonally.
System of orthogonal circles
The method described in the previous section for the construction of a pencil of circles, which intersect two given circles orthogonally, can be extended to the construction of two orthogonally intersecting systems of circles:[5][6]
Let be two apart lying circles (as in the previous section), their centers and radii and their radical axis. Now, all circles will be determined with centers on line , which have together with line as radical axis, too. If is such a circle, whose center has distance to the center and radius . From the result in the previous section one gets the equation
- , where are fixed.
With the equation can be rewritten as:
- .
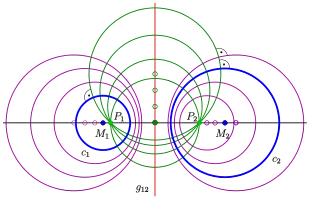
If radius is given, from this equation one finds the distance to the (fixed) radical axis of the new center. In the diagram the color of the new circles is purple. Any green circle (see diagram) has its center on the radical axis and intersects the circles orthogonally and hence all new circles (purple), too. Choosing the (red) radical axis as y-axis and line as x-axis, the two pencils of circles have the equations:
- purple:
- green:
( is the center of a green circle.)
Properties:
a) Any two green circles intersect on the x-axis at the points , the poles of the orthogonal system of circles. That means, the x-axis is the radical line of the green circles.
b) The purple circles have no points in common. But, if one considers the real plane as part of the complex plane, then any two purple circles intersect on the y-axis (their common radical axis) at the points .
Special cases:
a) In case of the green circles are touching each other at the origin with the x-axis as common tangent and the purple circles have the y-axis as common tangent. Such a system of circles is called coaxal parabolic circles (see below).
b) Shrinking to its center , i. e. , the equations turn into a more simple form and one gets .
Conclusion:
a) For any real the pencil of circles
- has the property: The y-axis is the radical axis of .
- In case of the circles intersect at points .
- In case of they have no points in common.
- In case of they touch at and the y-axis is their common tangent.
b) For any real the two pencils of circles
- form a system of orthogonal circles. That means: any two circles intersect orthogonally.
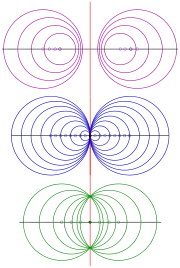
c) From the equations in b), one gets a coordinate free representation:
- For the given points , their midpoint and their line segment bisector the two equations
- with on , but not between , and on
- describe the orthogonal system of circles uniquely determined by which are the poles of the system.
- For one has to prescribe the axes of the system, too. The system is parabolic:
- with on and on .
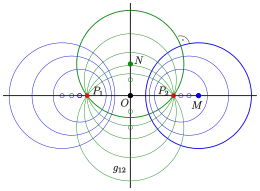
Straightedge and compass construction:
A system of orthogonal circles is determined uniquely by its poles :
- The axes (radical axes) are the lines and the Line segment bisector of the poles.
- The circles (green in the diagram) through have their centers on . They can be drawn easily. For a point the radius is .
- In order to draw a circle of the second pencil (in diagram blue) with center on , one determines the radius applying the theorem of Pythagoras: (see diagram).
In case of the axes have to be chosen additionally. The system is parabolic and can be drawn easily.
Coaxal circles
Definition and properties:
Let be two circles and their power functions. Then for any
is the equation of a circle (see below). Such a system of circles is called coaxal circles generated by the circles . (In case of the equation describes the radical axis of .) [7][8]
The power function of is
- .
The normed equation (the coefficients of are ) of is .
A simple calculation shows:
- have the same radical axis as .
Allowing to move to infinity, one recognizes, that are members of the system of coaxal circles: .
(E): If intersect at two points , any circle contains , too, and line is their common radical axis. Such a system is called elliptic.
(P): If are tangent at , any circle is tangent to at point , too. The common tangent is their common radical axis. Such a system is called parabolic.
(H): If have no point in common, then any pair of the system, too. The radical axis of any pair of circles is the radical axis of . The system is called hyperbolic.
In detail:
Introducing coordinates such that
- ,
then the y-axis is their radical axis (see above).
Calculating the power function gives the normed circle equation:
Completing the square and the substitution (x-coordinate of the center) yields the centered form of the equation
- .
In case of the circles have the two points
in common and the system of coaxal circles is elliptic.
In case of the circles have point in common and the system is parabolic.
In case of the circles have no point in common and the system is hyperbolic.
Alternative equations:
1) In the defining equation of a coaxal system of circles there can be used multiples of the power functions, too.
2) The equation of one of the circles can be replaced by the equation of the desired radical axis. The radical axis can be seen as a circle with an infinitely large radius. For example:
- ,
describes all circles, which have with the first circle the line as radical axis.
3) In order to express the equal status of the two circles, the following form is often used:
But in this case the representation of a circle by the parameters is not unique.
Applications:
a) Circle inversions and Möbius transformations preserve angles and generalized circles. Hence orthogonal systems of circles play an essential role with investigations on these mappings. [9][10]
b) In electromagnetism coaxal circles appear as field lines. [11]
Radical center of three circles, construction of the radical axis
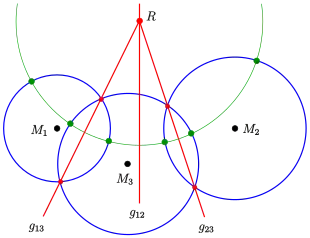
The green circle intersects the three circles orthogonally.
- For three circles , no two of which are concentric, there are three radical axes . If the circle centers do not lie on a line, the radical axes intersect in a common point , the radical center of the three circles. The orthogonal circle centered around of two circles is orthogonal to the third circle, too (radical circle).
- Proof: the radical axis contains all points which have equal tangential distance to the circles . The intersection point of and has the same tangential distance to all three circles. Hence is a point of the radical axis , too.
- This property allows one to construct the radical axis of two non intersecting circles with centers : Draw a third circle with center not collinear to the given centers that intersects . The radical axes can be drawn. Their intersection point is the radical center of the three circles and lies on . The line through which is perpendicular to is the radical axis .
Additional construction method:
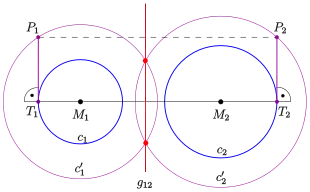
All points which have the same power to a given circle lie on a circle concentric to . Let us call it an equipower circle. This property can be used for an additional construction method of the radical axis of two circles:
For two non intersecting circles , there can be drawn two equipower circles , which have the same power with respect to (see diagram). In detail: . If the power is large enough, the circles have two points in common, which lie on the radical axis .
Relation to bipolar coordinates
In general, any two disjoint, non-concentric circles can be aligned with the circles of a system of bipolar coordinates. In that case, the radical axis is simply the -axis of this system of coordinates. Every circle on the axis that passes through the two foci of the coordinate system intersects the two circles orthogonally. A maximal collection of circles, all having centers on a given line and all pairs having the same radical axis, is known as a pencil of coaxal circles.
Radical center in trilinear coordinates
If the circles are represented in trilinear coordinates in the usual way, then their radical center is conveniently given as a certain determinant. Specifically, let X = x : y : z denote a variable point in the plane of a triangle ABC with sidelengths a = |BC|, b = |CA|, c = |AB|, and represent the circles as follows:
- (dx + ey + fz)(ax + by + cz) + g(ayz + bzx + cxy) = 0
- (hx + iy + jz)(ax + by + cz) + k(ayz + bzx + cxy) = 0
- (lx + my + nz)(ax + by + cz) + p(ayz + bzx + cxy) = 0
Then the radical center is the point
Radical plane and hyperplane
The radical plane of two nonconcentric spheres in three dimensions is defined similarly: it is the locus of points from which tangents to the two spheres have the same length.[12] The fact that this locus is a plane follows by rotation in the third dimension from the fact that the radical axis is a straight line.
The same definition can be applied to hyperspheres in Euclidean space of any dimension, giving the radical hyperplane of two nonconcentric hyperspheres.
Notes
- Michel Chasles, C. H. Schnuse: Die Grundlehren der neuern Geometrie, erster Theil, Verlag Leibrock, Braunschweig, 1856, p. 312
- Ph. Fischer: Lehrbuch der analytische Geometrie, Darmstadt 1851, Verlag Ernst Kern, p. 67
- H. Schwarz: Die Elemente der analytischen Geometrie der Ebene, Verlag H. W. Schmidt, Halle, 1858, p. 218
- Jakob Steiner: Einige geometrische Betrachtungen. In: Journal für die reine und angewandte Mathematik, Band 1, 1826, p. 165
- A. Schoenfliess, R. Courant: Einführung in die Analytische Geometrie der Ebene und des Raumes, Springer-Verlag, 1931, p. 113
- C. Carathéodory: Funktionentheorie, Birkhäuser-Verlag, Basel, 1961, ISBN 978-3-7643-0064-7, p. 46
- Dan Pedoe: Circles: A Mathematical View, mathematical Association of America, 2020, ISBN 9781470457327, p. 16
- R. Lachlan: An Elementary Treatise On Modern Pure Geometry, MacMillan&Co, New York,1893, p. 200
- Carathéodory: Funktionentheorie, p. 47.
- R. Sauer: Ingenieur-Mathematik: Zweiter Band: Differentialgleichungen und Funktionentheorie, Springer-Verlag, 1962, ISBN 978-3-642-53232-0, p. 105
- Clemens Schaefer: Elektrodynamik und Optik, Verlag: De Gruyter, 1950, ISBN 978-3-11-230936-0, p. 358.
- See Merriam–Webster online dictionary.
References
- R. A. Johnson (1960). Advanced Euclidean Geometry: An Elementary Treatise on the Geometry of the Triangle and the Circle (reprint of 1929 edition by Houghton Mifflin ed.). New York: Dover Publications. pp. 31–43. ISBN 978-0-486-46237-0.
Further reading
- C. Stanley Ogilvy (1990). Excursions in Geometry. Dover. pp. 17–23. ISBN 0-486-26530-7.
- H. S. M. Coxeter, S. L. Greitzer (1967). Geometry Revisited. Washington, D.C.: Mathematical Association of America. pp. 31–36, 160–161. ISBN 978-0-88385-619-2.
- Clark Kimberling, "Triangle Centers and Central Triangles," Congressus Numerantium 129 (1998) i–xxv, 1–295.