Rankine vortex

The Rankine vortex is a simple mathematical model of a vortex in a viscous fluid. It is named after its discoverer, William John Macquorn Rankine.

Velocity distribution in a Rankine vortex.

Animation of a Rankine vortex. Free-floating test particles reveal the velocity and vorticity pattern.

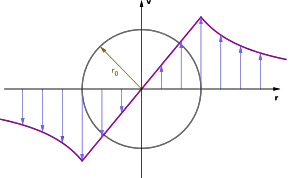
The vortices observed in nature are usually modelled with an irrotational (potential or free) vortex. However, in potential vortex, the velocity becomes infinite at the vortex center. In reality, very close to the origin, the motion resembles a solid body rotation. The Rankine vortex model assumes a solid-body rotation inside a cylinder of radius ${\displaystyle a}$ and a potential vortex outside the cylinder. The radius ${\displaystyle a}$ is referred to as the vortex-core radius. The velocity components ${\displaystyle (v_{r},v_{\theta },v_{z})}$ of the Rankine vortex, expressed in terms of the cylindrical-coordinate system ${\displaystyle (r,\theta ,z)}$ are given by[1]

${\displaystyle v_{r}=0,\quad v_{\theta }(r)={\frac {\Gamma }{2\pi }}{\begin{cases}r/a^{2}&r\leq a,\\1/r&r>a\end{cases}},\quad v_{z}=0}$

where ${\displaystyle \Gamma }$ is the circulation strength of the Rankine vortex. Since solid-body rotation is characterized by an azimuthal velocity ${\displaystyle \Omega r}$, where ${\displaystyle \Omega }$ is the constant angular velocity, one can also use the parameter ${\displaystyle \Omega =\Gamma /(2\pi a^{2})}$ to characterize the vortex.

The vorticity field ${\displaystyle (\omega _{r},\omega _{\theta },\omega _{z})}$ associated with the Rankine vortex is

${\displaystyle \omega _{r}=0,\quad \omega _{\theta }=0,\quad \omega _{z}={\begin{cases}2\Omega &r\leq a,\\0&r>a\end{cases}}.}$

At all points inside the core of the Rankine vortex, the vorticity is uniform at twice the angular velocity of the core; whereas vorticity is zero at all points outside the core because the flow there is irrotational.

In reality, vortex cores are not always circular; and vorticity is not exactly uniform throughout the vortex core.