Raviart–Thomas basis functions
In applied mathematics, Raviart–Thomas basis functions are vector basis functions used in finite element and boundary element methods. They are regularly used as basis functions when working in electromagnetics. They are sometimes called Rao-Wilton-Glisson basis functions.[1]
The space spanned by the Raviart–Thomas basis functions of order is the smallest polynomial space such that the divergence maps onto , the space of piecewise polynomials of order .[2]
Order 0 Raviart-Thomas Basis Functions in 2D
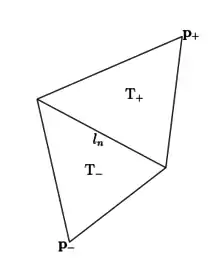
In two-dimensional space, the lowest order Raviart Thomas space, , has degrees of freedom on the edges of the elements of the finite element mesh. The th edge has an associated basis function defined by[3]
where is the length of the edge, and are the two triangles adjacent to the edge, and are the areas of the triangles and and are the opposite corners of the triangles.
Sometimes the basis functions are alternatively defined as
with the length factor not included.
References
- Andriulli, Francesco P.; Cools; Bagci; Olyslager; Buffa; Christiansen; Michelssen (2008). "A Mulitiplicative Calderon Preconditioner for the Electric Field Integral Equation". IEEE Transactions on Antennas and Propagation. 56 (8): 2398–2412. Bibcode:2008ITAP...56.2398A. doi:10.1109/tap.2008.926788. hdl:1854/LU-677703. S2CID 38745490.
- Logg, Anders; Mardal, Kent-Andre; Wells, Garth, eds. (2012). "Chapter 3. Common and unusual finite elements". Automated Solution of Differential Equations by the Finite Element Method. Lecture Notes in Computational Science and Engineering. Vol. 84. Berlin, Heidelberg: Springer Berlin Heidelberg. pp. 95–119. doi:10.1007/978-3-642-23099-8. ISBN 978-3-642-23098-1.
- Bahriawati, C.; Carstensen, C. (2005). "Three MATLAB Implementations Of The Lowest-Order Raviart-Thomas MFEM With a Posteriori Error Control" (PDF). Computational Methods in Applied Mathematics. 5 (4): 331–361. doi:10.2478/cmam-2005-0016. S2CID 3897312. Retrieved 8 October 2015.