Gnomonic projection
A gnomonic map projection is a map projection which displays all great circles as straight lines, resulting in any straight line segment on a gnomonic map showing a geodesic, the shortest route between the segment's two endpoints. This is achieved by casting surface points of the sphere onto a tangent plane, each landing where a ray from the center of the sphere passes through the point on the surface and then on to the plane. No distortion occurs at the tangent point, but distortion increases rapidly away from it. Less than half of the sphere can be projected onto a finite map.[1] Consequently, a rectilinear photographic lens, which is based on the gnomonic principle, cannot image more than 180 degrees.


History
The gnomonic projection is said to be the oldest map projection, developed by Thales for star maps in the 6th century BC[1]: 164 . The path of the shadow-tip or light-spot in a nodus-based sundial traces out the same hyperbolae formed by parallels on a gnomonic map.
Properties
The gnomonic projection is from the centre of a sphere to a plane tangent to the sphere (Fig 1 below). The sphere and the plane touch at the tangent point. Great circles transform to straight lines via the gnomonic projection. Since meridians (lines of longitude) and the equator are great circles, they are always shown as straight lines on a gnomonic map. Since the projection is from the centre of the sphere, a gnomonic map can represent less than half of the area of the sphere. Distortion of the scale of the map increases from the centre (tangent point) to the periphery.[1]
- If the tangent point is one of the poles then the meridians are radial and equally spaced (Fig 2 below). The equator cannot be shown as it is at infinity in all directions. Other parallels (lines of latitude) are depicted as concentric circles.
- If the tangent point is on the equator then the meridians are parallel but not equally spaced (Fig 3 below). The equator is a straight line perpendicular to the meridians. Other parallels are depicted as hyperbolae.
- If the tangent point is not on a pole or the equator, then the meridians are radially outward straight lines from a pole, but not equally spaced (Fig 4 below). The equator is a straight line that is perpendicular to only one meridian, indicating that the projection is not conformal. Other parallels are depicted as conic sections.
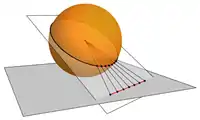 Fig 1. A great circle projects to a straight line in the gnomonic projection
Fig 1. A great circle projects to a straight line in the gnomonic projection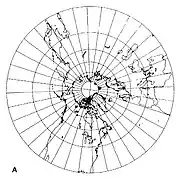 Fig 2. Gnomonic projection centred on the North Pole
Fig 2. Gnomonic projection centred on the North Pole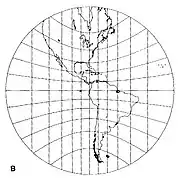 Fig 3. Gnomonic projection centred on the equator
Fig 3. Gnomonic projection centred on the equator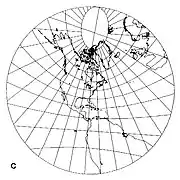 Fig 4. Gnomonic projection centred on latitude 40 deg North
Fig 4. Gnomonic projection centred on latitude 40 deg North
As with all azimuthal projections, angles from the tangent point are preserved. The map distance from that point is a function r(d) of the true distance d, given by
where R is the radius of the Earth. The radial scale is
and the transverse scale
so the transverse scale increases outwardly, and the radial scale even more.
Use
Gnomonic projections are used in seismic work because seismic waves tend to travel along great circles. They are also used by navies in plotting direction finding bearings, since radio signals travel along great circles. Meteors also travel along great circles, with the Gnomonic Atlas Brno 2000.0 being the IMO's recommended set of star charts for visual meteor observations. Aircraft and ship pilots use the projection to find the shortest route between start and destination.
The gnomonic projection is used extensively in photography, where it is called rectilinear projection. Because they are equivalent, the same viewer used for photographic panoramas can be used to render gnomonic maps (view as a 360° interactive panorama).
The gnomonic projection is used in astronomy where the tangent point is centered on the object of interest. The sphere being projected in this case is the celestial sphere, R = 1, and not the surface of the Earth.
In astronomy, gnomic projection star charts of the celestial sphere can be used by observers to accurately plot the straight line path of a meteor trail.[2]
See also
- Local tangent plane
- List of map projections
- Beltrami–Klein model, the analogous mapping of the hyperbolic plane
References
- Snyder, John P. (1987). Map Projections – A Working Manual. U.S. Geological Survey Professional Paper 1395. Washington, D.C: United States Government Printing Office. pp. 164–168. doi:10.3133/pp1395.
- Taibi, Richard (November 25, 2016), Charles Olivier and the Rise of Meteor Science, Springer International Publishing, p. 67, ISBN 9783319445182.
- Calabretta, Mark R.; Greisen, Eric W. (July 19, 2002). "Representations of celestial coordinates in FITS (Paper II)". Astronomy & Astrophysics. 395: 1077–1122. arXiv:astro-ph/0207413. doi:10.1051/0004-6361:20021327. S2CID 18019255.
