Smoothed octagon

The corners of the smoothed octagon can be found by rotating three regular octagons whose centres form a triangle with constant area.

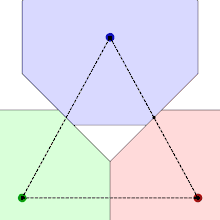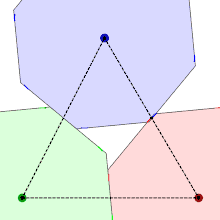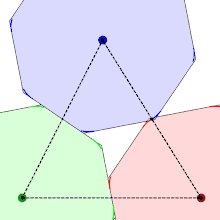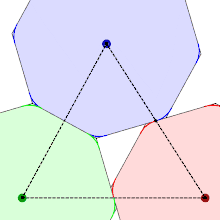
The shape of the smoothed octagon can be derived from its packings, which place octagons at the points of a hexagonal lattice. The requirement that these packings have the same density no matter how the lattice and smoothed octagon are rotated relative to each other, with shapes that remain in contact with each neighboring shape, can be used to determine the shape of the corners. One of the figures shows three octagons that rotate while the area of the triangle formed by their centres remains constant, keeping them packed together as closely as possible. For regular octagons, the red and blue shapes would overlap, so to enable the rotation to proceed the corners are clipped to a point that lies halfway between their centres, generating the required curve, which turns out to be a hyperbola.

Construction of the smoothed octagon (black), the tangent hyperbola (red), the asymptotes of this hyperbola (green), and the tangent sides to the hyperbola (blue)

The hyperbola is constructed tangent to two sides of the octagon, and asymptotic to the two adjacent to these.[3] The following details apply to a regular octagon of circumradius ${\displaystyle {\sqrt {2}}}$ with its centre at the point ${\displaystyle (2+{\sqrt {2}},0)}$ and one vertex at the point ${\displaystyle (2,0)}$. For two constants ${\displaystyle \ell ={\sqrt {2}}-1}$ and ${\displaystyle m=(1/2)^{1/4}}$, the hyperbola is given by the equation

$${\displaystyle \ell ^{2}x^{2}-y^{2}=m^{2}}$$

or the equivalent parameterization (for the right-hand branch only)

$${\displaystyle {\begin{aligned}x&={\frac {m}{\ell }}\cosh {t}\\y&=m\sinh {t}\\\end{aligned}}}$$

for the portion of the hyperbola that forms the corner, given by the range of parameter values

$${\displaystyle -{\frac {\ln {2}}{4}}<t<{\frac {\ln {2}}{4}}.}$$

The lines of the octagon tangent to the hyperbola are ${\displaystyle y=\pm \left({\sqrt {2}}+1\right)\left(x-2\right)}$, and the lines asymptotic to the hyperbola are simply ${\displaystyle y=\pm \ell x}$.

For every centrally symmetric convex planar set, including the smoothed octagon, the maximum packing density is achieved by a lattice packing, in which unrotated copies of the shape are translated by the vectors of a lattice.[4] The smoothed octagon achieves its maximum packing density, not just for a single packing, but for a 1-parameter family. All of these are lattice packings.[5] The smoothed octagon has a maximum packing density given by[2][3]

$${\displaystyle {\frac {8-4{\sqrt {2}}-\ln {2}}{2{\sqrt {2}}-1}}\approx 0.902414\,.}$$

This is lower than the maximum packing density of circles, which is[3]

$${\displaystyle {\frac {\pi }{\sqrt {12}}}\approx 0.906899.}$$

The maximum known packing density of the ordinary regular octagon is

$${\displaystyle {\frac {4+4{\sqrt {2}}}{5+4{\sqrt {2}}}}\approx 0.906163,}$$

also slightly less than the maximum packing density of circles, but higher than that of the smoothed octagon.[6]

Reinhardt's conjecture that the smoothed octagon has the lowest maximum packing density of all centrally symmetric convex shapes in the plane remains unsolved. As a partial result, Fedor Nazarov proved that the smoothed octagon has a local minimum of packing density among these shapes.[7]

If central symmetry is not required, the regular heptagon is conjectured to have even lower packing density, but neither its packing density nor its optimality have been proven. In three dimensions, Ulam's packing conjecture states that no convex shape has a lower maximum packing density than the ball.[5]

• Packing smoothed octagons. John Baez, Visual Insight, AMS Blogs, 2014.
• The thinnest densest two-dimensional packing?. Peter Scholl, 2001.