Rigid line inclusion

A rigid line inclusion, also called stiffener, is a mathematical model used in solid mechanics to describe a narrow hard phase, dispersed within a matrix material. This inclusion is idealised as an infinitely rigid and thin reinforcement, so that it represents a sort of ‘inverse’ crack, from which the nomenclature ‘anticrack’ derives.

From the mechanical point of view, a stiffener introduces a kinematical constraint, imposing that it may only suffer a rigid body motion along its line.

Theoretical model

The stiffener model has been used to investigate different mechanical problems in classical elasticity (load diffusion,[1] inclusion at bi material interface [2]).

Sketch of a stiffener embedded in a matrix loaded at its boundary.

The main characteristics of the theoretical solutions are basically the following.

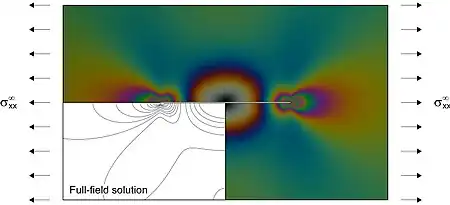
  1. Similarly to a fracture, a square-root singularity in the stress/strain fields is present at the tip of the inclusion.
  2. In a homogeneous matrix subject to uniform stress at infinity, such singularity only arises when a normal stress acts parallel or orthogonal to the inclusion line, while a stiffener parallel to a simple shear does not disturb the ambient field.

Experimental validation
Dog-bone shaped sample of two-component epoxy resin containing a lamellar (aluminum) inclusion.
Photoelastic experiment to validate the rigid line inclusion model. Isochromatic fringe patterns around a steel platelet in a photo-elastic two-part epoxy resin compared to analytical solution obtained in plane-strain classical elasticity. Normal stress parallel to the inclusion line is applied.

The characteristics of the elastic solution have been experimentally confirmed through photoelastic transmission experiments.[3]

Interaction of rigid line inclusions

The interaction of rigid line inclusions in parallel, collinear and radial configurations have been studied using the boundary element method (BEM) and validated using photoelasticity.[4]

Shear bands emerging at the stiffener tip

Analytical solutions obtained in prestressed elasticity show the possibility of the emergence of shear bands at the tip of the stiffener.[5][6][7][8]

References
  1. Koiter, W.T., On the diffusion of load from a stiffener into a sheet. Q. J. Mech. Appl. Math. 1955, VIII, 164–178.
  2. Ballarini, R., A rigid line inclusion at a bimaterial interface. Eng. Fract. Mech., 1990, 37, 1–5.
  3. G. Noselli, F. Dal Corso and D. Bigoni, The stress intensity near a stiffener disclosed by photoelasticity. International Journal of Fracture, 2010, 166, 91–103.
  4. Jobin, T. M., M. Ramji, and S. N. Khaderi. "Numerical evaluation of the interaction of rigid line inclusions using strain intensity factors." International Journal of Mechanical Sciences 153 (2019): 10-20.
  5. Bigoni, D. Nonlinear Solid Mechanics: Bifurcation Theory and Material Instability. Cambridge University Press, 2012 . ISBN 9781107025417.
  6. F. Dal Corso, D. Bigoni and M. Gei, The stress concentration near a rigid line inclusion in a prestressed, elastic material. Part I Full-field solution and asymptotics. Journal of the Mechanics and Physics of Solids, 2008, 56, 815–838.
  7. D. Bigoni, F. Dal Corso and M. Gei, The stress concentration near a rigid line inclusion in a prestressed, elastic material. Part II Implications on shear band nucleation, growth and energy release rate. Journal of the Mechanics and Physics of Solids, 2008, 56, 839–857.
  8. F. Dal Corso and D. Bigoni, The interactions between shear bands and rigid lamellar inclusions in a ductile metal matrix. Proceedings of the Royal Society A, 2009, 465, 143–163.
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.