Robot kinematics

In robotics, robot kinematics applies geometry to the study of the movement of multi-degree of freedom kinematic chains that form the structure of robotic systems.[1][2] The emphasis on geometry means that the links of the robot are modeled as rigid bodies and its joints are assumed to provide pure rotation or translation.

Inverse kinematics of SCARA robot done with MeKin2D.

Robot kinematics studies the relationship between the dimensions and connectivity of kinematic chains and the position, velocity and acceleration of each of the links in the robotic system, in order to plan and control movement and to compute actuator forces and torques. The relationship between mass and inertia properties, motion, and the associated forces and torques is studied as part of robot dynamics.

Kinematic equations
Further information: Kinematic equation

A fundamental tool in robot kinematics is the kinematics equations of the kinematic chains that form the robot. These non-linear equations are used to map the joint parameters to the configuration of the robot system. Kinematics equations are also used in biomechanics of the skeleton and computer animation of articulated characters.

Forward kinematics uses the kinematic equations of a robot to compute the position of the end-effector from specified values for the joint parameters.[3] The reverse process that computes the joint parameters that achieve a specified position of the end-effector is known as inverse kinematics. The dimensions of the robot and its kinematics equations define the volume of space reachable by the robot, known as its workspace.

There are two broad classes of robots and associated kinematics equations: serial manipulators and parallel manipulators. Other types of systems with specialized kinematics equations are air, land, and submersible mobile robots, hyper-redundant, or snake, robots and humanoid robots.

Forward kinematics
Forward kinematics of an over-actuated planar parallel manipulator done with MeKin2D.
Main article: Forward kinematics

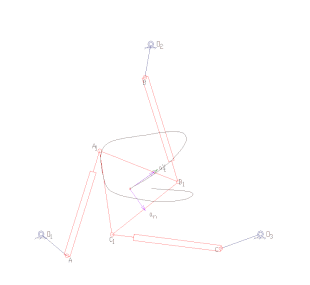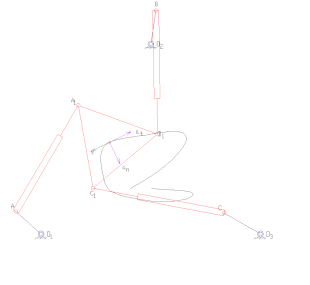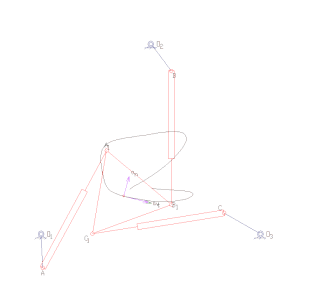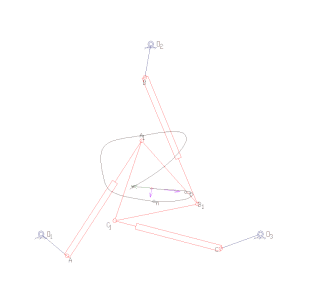
Forward kinematics specifies the joint parameters and computes the configuration of the chain. For serial manipulators this is achieved by direct substitution of the joint parameters into the forward kinematics equations for the serial chain. For parallel manipulators substitution of the joint parameters into the kinematics equations requires solution of the a set of polynomial constraints to determine the set of possible end-effector locations.

Inverse kinematics
Main article: Inverse kinematics

Inverse kinematics specifies the end-effector location and computes the associated joint angles. For serial manipulators this requires solution of a set of polynomials obtained from the kinematics equations and yields multiple configurations for the chain. The case of a general 6R serial manipulator (a serial chain with six revolute joints) yields sixteen different inverse kinematics solutions, which are solutions of a sixteenth degree polynomial. For parallel manipulators, the specification of the end-effector location simplifies the kinematics equations, which yields formulas for the joint parameters.

Robot Jacobian

The time derivative of the kinematics equations yields the Jacobian of the robot, which relates the joint rates to the linear and angular velocity of the end-effector. The principle of virtual work shows that the Jacobian also provides a relationship between joint torques and the resultant force and torque applied by the end-effector. Singular configurations of the robot are identified by studying its Jacobian.

Velocity kinematics

The robot Jacobian results in a set of linear equations that relate the joint rates to the six-vector formed from the angular and linear velocity of the end-effector, known as a twist. Specifying the joint rates yields the end-effector twist directly.

The inverse velocity problem seeks the joint rates that provide a specified end-effector twist. This is solved by inverting the Jacobian matrix. It can happen that the robot is in a configuration where the Jacobian does not have an inverse. These are termed singular configurations of the robot.

Static force analysis

The principle of virtual work yields a set of linear equations that relate the resultant force-torque six vector, called a wrench, that acts on the end-effector to the joint torques of the robot. If the end-effector wrench is known, then a direct calculation yields the joint torques.

The inverse statics problem seeks the end-effector wrench associated with a given set of joint torques, and requires the inverse of the Jacobian matrix. As in the case of inverse velocity analysis, at singular configurations this problem cannot be solved. However, near singularities small actuator torques result in a large end-effector wrench. Thus near singularity configurations robots have large mechanical advantage.

Fields of study

Robot kinematics also deals with motion planning, singularity avoidance, redundancy, collision avoidance, as well as the kinematic synthesis of robots.[4]

See also

References
  1. Paul, Richard (1981). Robot manipulators: mathematics, programming, and control : the computer control of robot manipulators. MIT Press, Cambridge, Massachusetts. ISBN 978-0-262-16082-7.
  2. J. M. McCarthy, 1990, Introduction to Theoretical Kinematics, MIT Press, Cambridge, Massachusetts.
  3. John J. Craig, 2004, Introduction to Robotics: Mechanics and Control (3rd Edition), Prentice-Hall.
  4. J. M. McCarthy and G. S. Soh, Geometric Design of Linkages, 2nd Edition, Springer 2010.
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.