Salinon

The salinon (meaning 'salt-cellar' in Greek) is a geometrical figure that consists of four semicircles. It was first introduced in the Book of Lemmas, a work attributed to Archimedes.[1]

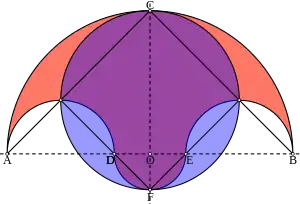
The salinon (red) and the circle (blue) have the same area.

Construction

Let A, D, E, and B be four points on a line in the plane, in that order, with AD = EB. Let O be the bisector of segment AB (and of DE). Draw semicircles above line AB with diameters AB, AD, and EB, and another semicircle below with diameter DE. A salinon is the figure bounded by these four semicircles.[2]

Properties

Area

Archimedes introduced the salinon in his Book of Lemmas by applying Book II, Proposition 10 of Euclid's Elements. Archimedes noted that "the area of the figure bounded by the circumferences of all the semicircles [is] equal to the area of the circle on CF as diameter."[3]

Namely, if is the radius of large enclosing semicircle, and is the radius of the small central semicircle, then the area of the salinon is:[4]

Arbelos

Should points D and E converge with O, it would form an arbelos, another one of Archimedes' creations, with symmetry along the y-axis.[3]

See also

References
  1. Heath, T. L. (1897). "On the Salinon of Archimedes". The Journal of Philology. 25 (50): 161–163.
  2. Nelsen, Roger B. (April 2002). "Proof without words: The area of a salinon". Mathematics Magazine. 75 (2): 130. doi:10.2307/3219147. JSTOR 3219147.
  3. Bogomolny, Alexander. "Salinon: From Archimedes' Book of Lemmas". Cut-the-knot. Retrieved 2008-04-15.
  4. Weisstein, Eric W. "Salinon". MathWorld.
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.