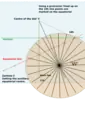
Schema for vertical declining dials

Vertical declining dials are sundials that indicate local apparent time. Vertical south dials are a special case: as are vertical north, vertical east and vertical west dials. The word declining means that the wall is offset from one of these 4 cardinal points. There are dials that are not vertical, and these are called reclining dials.[1]

A dial constructed using Waugh's schema

A sundial schema uses a compass and a straight edge to firstly derive the essential angles for that latitude, then to use this to draw the hourlines on the dial plate. In modern terminology this would mean that graphical techniques were used to derive $\sin x$ and $m\tan y$ and from it $\sin x.\tan y$ . [lower-alpha 1]

Basic calculation

There are four basic angles that are needed to construct a vertical declining dial, Waugh described them such: [2]

SD- Sub-style distance - this is the angle on the dial plate between the foot of the style and the vertical noon line.
SH- Sub-style height - this defines the slope of the style. It has no effect on the design of the dial plate.
DL- Difference in longitude- in drawing the dial, DL represents the hour/angle (polar angle)Holwell, John (1712). Clavis Horologiae. [lower-alpha 2] when the shadow passes under the style.
AV- Angle to vertical? -this is used to fix a starting point, in the final stage of laying out equal hours with a protractor. With a calculator this can be easily be derived from the SD and DL, when using compass and ruler it is a construction base line. It never appears on the final dial.

The four basic calculation have a certain symmetry.

tan (SD) = sin (D). cot(φ)
sin (SH) = cos (D). cos(φ)
cot (DL) = cot (D). sin(φ)
cot (AV) = sin (D). tan(φ)

Waugh's method 1973

A semicircle is drawn, with a descending vertical.
For a morning dial, or south-east declining dial, a right angled triangle is drawn to the left with the top angle being the co-latitude.
A second triangle is drawn to the right, with a top angle of D, the declination of the wall.

Finding SD- the substyle length

The bottom bar of the left triangle represents cot Φ. The length is noted and using dividers copied over to the hypotenuse of the right triangle, and a further horizontal bar drawn; that will have the length of sin D. This is measured and placed on the bottom bar of the left triangle. This sets the position M, and the substyle line (the term diallist use for the angle).

Finding SH - the substyle height

The height of the right triangle is noted, and a line of this length is swung from point M, till it touches the circle. The angle from the origin to here, is the substyle height.(the term diallist use for the angle).[lower-alpha 3]

Drawing the hourlines

At this point only three lines matter, the vertical, the substyle length and substyle height. A circle marked off in 15° angles is needed (circular protractor).

An arbitrary point on the sub-style line is chosen. From here, a long-line, at right-angles to it, is drawn. A line is drawn at right angles from the substyle height, so that it passes through that point. Its length is noted.
The length is copied from the point to O'. This will become the centre used by circular protractor. Draw a line from here to crossing of the vertical and the long-line.
The circular protractor is aligned so that zero falls on the new line. Points are marked off and lines drawn through them to the long line. From each of these crossings. a final line is drawn back to the Origin at the top. These are the hour-lines. 12 is on the vertical, and the forenoon hours are to the left- and the afternoon hours (fewer in number) to the right. [3]

Wigham-Richardson's method

Before the protractor became ubiquitous, compasses and the Scale of Chords were used for laying out an angle. This method originally used them.

A large cross is drawn, ACB being the vertical line and PCQ horizontally.
Two arcs are drawn to the right - AQ, and CT.
Two triangle are drawn ACT- with the co-latitude (90- Φ) at the top, and CWX- with the declination 'D' at the centre. For the example these will be 38° and 20°

Finding SD

A line is drawn from X through C to a point that will be eventually named S. Take compasses and using the radius CD swing an clockwise arc to this line, where it cuts is the point S. In other words CS is equal in length to CD.
Drop a perpendicular line (RS) from line PQ to cut through S. To fix the point Y: copy the length RS, from C onto the line PQ. This is CY. RS=CY.
Join A to Y. This is the substyle distance SD.

Finding SH and the centre of the equinoctial

A long line, perpendicular to AY is drawn- it will take the points G,Y,P and M. YG is equal in length to CR. Join AG and the angle YAG is the substyle height.

Drawing the hourlines

At this point only three lines matter, the vertical, the substyle length and substyle height. A circle marked off in 15° angles is needed (circular protractor).

A perpendicular line through Y is dropped from the sub-style line- the crossing is marked 'g '.
Compasses are used to transfer this length onto the substyle line. The point is called 'O' ', this is the centre of the equinoctial circle- a long line F F' is drawn perpendicularly.
Centre the circular protractor on O', with one line passing through P- call this XII.
From A the actual hour-lines through each of the points (stars) where the protractor lines cross G,Y,P and M.[4]

Use of Dialing rulers

Foster Serles Dialling Scales (1638) Foster is credited for producing a set of scales to assist in the laying out of the hour line on a dial. To use them SH and SD must already be known. The scales are placed on the SD line, and lines are drawn using the calculated SH value rather than the actual latitude.

Zarbula method

Zarbula is credited with the design of over a hundred sundials in Hautes Alpes and Piedmont. This region straddles the 45 ° parallel and as such his dials are a special case. He worked directly on the wall, and didn't require to know the latitude or the declination of the dial, these we found by observation. His dials were examples of frescos, and all gave five-minute accuracy.

Laying out the dial

With a plumb bob he drew a vertical line on the wall. This is the Noon Line.
He hammered a rod into the wall at right angles to the vertical. This is known as the centre of the dial, C
He observed and marked the shadow thrown by the tip of that rod, throughout a day. This line, technically known as a hyperbolic declination line.[lower-alpha 4]
Using a set of compasses, he determines the line of symmetry on the wall.[lower-alpha 5] This is the substyle line.[lower-alpha 6]

All the rest of the dial was laid out using a 45° square, with a 15° measure at the end. [lower-alpha 7]

He drew a horizontal line at a point of choice on the dial plate. This was the Horizon.
The square was placed on the substyle facing outwards, it is slid into any convenient position where it cuts the horizon, and he drew a perpendicular line drawn to that point. This line is called the equatorial. A line was drawn from that point to the centre of the dial; it was the 18h line (or 6h depending on the declination (d) of the wall). The points where the equatorial crosses the noon line and where the equatorial crosses the substyle line were important.
He placed apex of the square on the substyle line, so the sides passed through the equatorial points mentioned. (The 12h and 18h markers). The apex point is called the auxiliary equatorial centre.
A protractor or squares [lower-alpha 8] drew off 15° intervals on the equatorial. These were connected to the centre of the dial: the hour lines. The distance from the auxiliary equatorial centre to the equatorial formed the substyle height at that point.[5][6]

References

Footnotes

The British Sundial Society publishes a glossary of computer terms and the symbols that are commonly used to represent them. Latitude is represented by phi, $\phi$ or φ or Φ.
This is in degrees- divide by 15 to convert to hours.
Waugh in his description is far more mathematically rigorous.
Declination of the sun ( δ ) not declination of the wall (d)
Indian or Hindu Circle for Sub-style determination
In dialling language substyle is used like sub aqua, meaning- under the style- not like subsection, meaning a smaller part. Similarly, equation means an adjustment and height can mean a perpendicular angle.
Zarbula was working within 2° of the 45th parallel, so it worked. Further north or south the triangle would need to use the latitude and co-latitude and a protractor would have been needed
A combination of a 30°/ 60° square, and 45° square could also be used.

Notes

Waugh 1973, Chapter 11.
Waugh 1973, pp. 78–79.
Waugh 1973, pp. 76–78.
Wigham-Richardson, J (1900). "APPENDIX ON THE CONSTRUCTION OF SUN-DIALS". In Gatty, Margaret Scott (Mrs Alfred) (ed.). The Book of Sun-dials (4th ed.). London: George Bell & Sons. pp. 487–499.
"L'Equerre et l'Oiseau".
Paul Gagnaire. "L'Équerre et l'Oiseau, l'Art et la Manière de Zarbula".

Bibliography

Waugh, Albert E. (1973). Sundials : their theory and construction. New York: Dover. ISBN 0486229475.

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.

[2] The British Sundial Society publishes a glossary of computer terms and the symbols that are commonly used to represent them. Latitude is represented by phi, $\phi$ or φ or Φ.

[4] This is in degrees- divide by 15 to convert to hours.

[5] Waugh in his description is far more mathematically rigorous.

[8] Declination of the sun ( δ ) not declination of the wall (d)

[9] Indian or Hindu Circle for Sub-style determination

[10] In dialling language substyle is used like sub aqua, meaning- under the style- not like subsection, meaning a smaller part. Similarly, equation means an adjustment and height can mean a perpendicular angle.

[11] Zarbula was working within 2° of the 45th parallel, so it worked. Further north or south the triangle would need to use the latitude and co-latitude and a protractor would have been needed

[12] A combination of a 30°/ 60° square, and 45° square could also be used.

[FOOTNOTEWaugh1973Chapter_11-1] Waugh 1973, Chapter 11.

[FOOTNOTEWaugh197378–79-3] Waugh 1973, pp. 78–79.

[FOOTNOTEWaugh197376–78-6] Waugh 1973, pp. 76–78.

[WR-7] Wigham-Richardson, J (1900). "APPENDIX ON THE CONSTRUCTION OF SUN-DIALS". In Gatty, Margaret Scott (Mrs Alfred) (ed.). The Book of Sun-dials (4th ed.). London: George Bell & Sons. pp. 487–499.

[13] "L'Equerre et l'Oiseau".

[gagnaire-14] Paul Gagnaire. "L'Équerre et l'Oiseau, l'Art et la Manière de Zarbula".

Time measurement and standards
Chronometry Orders of magnitude Metrology
International standards	Coordinated Universal Time offset UT ΔT DUT1 International Earth Rotation and Reference Systems Service ISO 31-1 ISO 8601 International Atomic Time 12-hour clock 24-hour clock Barycentric Coordinate Time Barycentric Dynamical Time Civil time Daylight saving time Geocentric Coordinate Time International Date Line IERS Reference Meridian Leap second Solar time Terrestrial Time Time zone 180th meridian
Obsolete standards	Ephemeris time Greenwich Mean Time Prime meridian
Time in physics	Absolute space and time Spacetime Chronon Continuous signal Coordinate time Cosmological decade Discrete time and continuous time Proper time Theory of relativity Time dilation Gravitational time dilation Time domain Time translation symmetry T-symmetry
Horology	Clock Astrarium Atomic clock Complication History of timekeeping devices Hourglass Marine chronometer Marine sandglass Radio clock Watch stopwatch Water clock Sundial Dialing scales Equation of time History of sundials Sundial markup schema
Calendar	Gregorian Hebrew Hindu Holocene Islamic (lunar Hijri) Julian Solar Hijri Astronomical Dominical letter Epact Equinox Intercalation Julian date Leap year Lunar Lunisolar Solar Solstice Tropical year Weekday determination Weekday names
Archaeology and geology	Chronological dating Geologic time scale International Commission on Stratigraphy
Astronomical chronology	Galactic year Nuclear timescale Precession Sidereal time
Other units of time	Instant Flick Shake Jiffy Second Minute Moment Hour Day Week Fortnight Month Year Olympiad Lustrum Decade Century Saeculum Millennium
Related topics	Chronology Duration music Mental chronometry Decimal time Metric time System time Time metrology Time value of money Timekeeper