Schiffler point

In geometry, the Schiffler point of a triangle is a triangle center, a point defined from the triangle that is equivariant under Euclidean transformations of the triangle. This point was first defined and investigated by Schiffler et al. (1985).

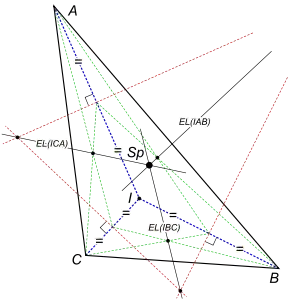
Diagram of the Schiffler point on an arbitrary triangle
Diagram of the Schiffler Point
  Triangle △ABC
  Angle bisectors; concur at incenter I
  Lines joining the midpoints of each angle bisector to the vertices of △ABC
  Lines perpendicular to each angle bisector at their midpoints
  Euler lines; concur at the Schiffler point Sp

Definition

A triangle △ABC with the incenter I has its Schiffler point at the point of concurrence of the Euler lines of the four triangles △BCI, △CAI, △ABI, △ABC. Schiffler's theorem states that these four lines all meet at a single point.

Coordinates

Trilinear coordinates for the Schiffler point are

or, equivalently,

where a, b, c denote the side lengths of triangle △ABC.

References
  • Emelyanov, Lev; Emelyanova, Tatiana (2003). "A note on the Schiffler point". Forum Geometricorum. 3: 113–116. MR 2004116.
  • Hatzipolakis, Antreas P.; van Lamoen, Floor; Wolk, Barry; Yiu, Paul (2001). "Concurrency of four Euler lines". Forum Geometricorum. 1: 59–68. MR 1891516.
  • Nguyen, Khoa Lu (2005). "On the complement of the Schiffler point". Forum Geometricorum. 5: 149–164. MR 2195745.
  • Schiffler, Kurt (1985). "Problem 1018" (PDF). Crux Mathematicorum. 11: 51. Retrieved September 24, 2023.
  • Veldkamp, G. R. & van der Spek, W. A. (1986). "Solution to Problem 1018" (PDF). Crux Mathematicorum. 12: 150–152. Retrieved September 24, 2023.
  • Thas, Charles (2004). "On the Schiffler center". Forum Geometricorum. 4: 85–95. MR 2081772.
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.