Shockley–Queisser limit
In physics, the radiative efficiency limit (also known as the detailed balance limit, Shockley–Queisser limit, Shockley Queisser Efficiency Limit or SQ Limit) is the maximum theoretical efficiency of a solar cell using a single p-n junction to collect power from the cell where the only loss mechanism is radiative recombination in the solar cell. It was first calculated by William Shockley and Hans-Joachim Queisser at Shockley Semiconductor in 1961, giving a maximum efficiency of 30% at 1.1 eV.[1] The limit is one of the most fundamental to solar energy production with photovoltaic cells, and is considered to be one of the most important contributions in the field.[2]

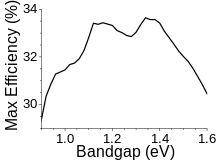
This first calculation used the 6000K black-body spectrum as an approximation to the solar spectrum. Subsequent calculations have used measured global solar spectra, AM 1.5, and included a back surface mirror which increases the maximum solar conversion efficiency to 33.16% for a single-junction solar cell with a bandgap of 1.34 eV.[3] That is, of all the power contained in sunlight (about 1000 W/m2) falling on an ideal solar cell, only 33.7% of that could ever be turned into electricity (337 W/m2). The most popular solar cell material, silicon, has a less favorable band gap of 1.1 eV, resulting in a maximum efficiency of about 32%. Modern commercial mono-crystalline solar cells produce about 24% conversion efficiency, the losses due largely to practical concerns like reflection off the front of the cell and light blockage from the thin wires on the cell surface.
The Shockley–Queisser limit only applies to conventional solar cells with a single p-n junction; solar cells with multiple layers can (and do) outperform this limit, and so can solar thermal and certain other solar energy systems. In the extreme limit, for a multi-junction solar cell with an infinite number of layers, the corresponding limit is 68.7% for normal sunlight,[4] or 86.8% using concentrated sunlight[5] (see solar cell efficiency).
Background
In a traditional solid-state semiconductor such as silicon, a solar cell is made from two doped crystals, one an n-type semiconductor, which has extra free electrons, and the other a p-type semiconductor, which is lacking free electrons, referred to as "holes." When initially placed in contact with each other, some of the electrons in the n-type portion will flow into the p-type to "fill in" the missing electrons. Eventually enough will flow across the boundary to equalize the Fermi levels of the two materials. The result is a region at the interface, the p-n junction, where charge carriers are depleted on each side of the interface. In silicon, this transfer of electrons produces a potential barrier of about 0.6 V to 0.7 V.[6]
When the material is placed in the sun, photons from the sunlight can be absorbed in the p-type side of the semiconductor, causing electrons in the valence band to be promoted in energy to the conduction band. This process is known as photoexcitation. As the name implies, electrons in the conduction band are free to move about the semiconductor. When a load is placed across the cell as a whole, these electrons will flow from the p-type side into the n-type side, lose energy while moving through the external circuit, and then go back into the p-type material where they can re-combine with the valence-band holes they left behind. In this way, sunlight creates an electric current.[6]
The limit
The Shockley–Queisser limit is calculated by examining the amount of electrical energy that is extracted per photon of incoming sunlight. There are several considerations:
Blackbody radiation
Any material, that is not at absolute zero (0 Kelvin), emits electromagnetic radiation through the black-body radiation effect. In a cell at room temperature, this represents approximately 7% of all the energy falling on the cell.
Any energy lost in a cell is turned into heat, so any inefficiency in the cell increases the cell temperature when it is placed in sunlight. As the temperature of the cell increases, the outgoing radiation and heat loss through conduction and convection also increase, until an equilibrium is reached. In practice, this equilibrium is normally reached at temperatures as high as 360 Kelvin, and consequently, cells normally operate at lower efficiencies than their room-temperature rating. Module datasheets normally list this temperature dependency as TNOCT (NOCT - Nominal Operating Cell Temperature).
For a "blackbody" at normal temperatures, a very small part of this radiation (the number per unit time and per unit area given by Qc, "c" for "cell") is photons having energy greater than the band gap (wavelength less than about 1.1 microns for silicon), and part of these photons (Shockley and Queisser use the factor tc) are generated by recombination of electrons and holes, which decreases the amount of current that could be generated otherwise. This is a very small effect, but Shockley and Queisser assume that the total rate of recombination (see below) when the voltage across the cell is zero (short circuit or no light) is proportional to the blackbody radiation Qc. This rate of recombination plays a negative role in the efficiency. Shockley and Queisser calculate Qc to be 1700 photons per second per square centimetre for silicon at 300K.
Recombination

Absorption of a photon creates an electron-hole pair, which could potentially contribute to the current. However, the reverse process must also be possible, according to the principle of detailed balance: an electron and a hole can meet and recombine, emitting a photon. This process reduces the efficiency of the cell. Other recombination processes may also exist (see "Other considerations" below), but this one is absolutely required.
In the Shockley–Queisser model, the recombination rate depends on the voltage across the cell but is the same whether or not there is light falling on the cell. A factor fc gives the ratio of recombination that produces radiation to total recombination, so the rate of recombination per unit area when V = 0 is 2tcQc/fc and thus depends on Qc, the flux of blackbody photons above the band-gap energy. The factor of 2 was included on the assumption that radiation emitted by the cell goes in both directions. (This is actually debatable if a reflective surface is used on the shady side.) When the voltage is non-zero, the concentrations of charge carriers (electrons and holes) change (see Shockley diode equation), and according to the authors the rate of recombination changes by a factor of exp(V/Vc), where Vc is the voltage equivalent of the temperature of the cell, or "thermal voltage", namely
(q being the charge of an electron). Thus the rate of recombination, in this model, is proportional to exp(V/Vc) times the blackbody radiation above the band-gap energy:
(This is actually an approximation, correct so long as the cell is thick enough to act as a black body, to the more accurate expression[7][8]
The difference in maximum theoretical efficiency however is negligibly small, except for tiny bandgaps below 200meV.[9])
The rate of generation of electron-hole pairs not due to incoming sunlight stays the same, so recombination minus spontaneous generation is
where
(Shockley and Queisser take fc to be a constant, although they admit that it may itself depend on voltage.)
The rate of generation of electron-hole pairs due to sunlight is
where is the number of photons above the band-gap energy falling on the cell per unit area, and ts is the fraction of these that generate an electron-hole pair. This rate of generation is called Ish because it is the "short circuit" current (per unit area). When there is a load, then V will not be zero and we have a current equal to the rate of generation of pairs due to the sunlight minus the difference between recombination and spontaneous generation:
The open-circuit voltage is therefore given (assuming fc does not depend on voltage) by
The product of the short-circuit current Ish and the open-circuit voltage Voc Shockley and Queisser call the "nominal power". It is not actually possible to get this amount of power out of the cell, but we can get close (see "Impedance matching" below).
The ratio of the open-circuit voltage to the band-gap voltage Shockley and Queisser call V. Under open-circuit conditions, we have
Asymptotically, this gives
or
where Vs is the voltage equivalent of the temperature of the sun. As the ratio Vc/Vs goes to zero, the open-circuit voltage goes to the band-gap voltage, and as it goes to one, the open-circuit voltage goes to zero. This is why the efficiency falls if the cell heats up. In fact this expression represents the thermodynamic upper limit of the amount of work that can be obtained from a heat source at the temperature of the sun and a heat sink at the temperature of the cell.
Spectrum losses
Since the act of moving an electron from the valence band to the conduction band requires energy, only photons with more than that amount of energy will produce an electron-hole pair. In silicon the conduction band is about 1.1 eV away from the valence band, this corresponds to infrared light with a wavelength of about 1.1 microns. In other words, photons of red, yellow and blue light and some near-infrared will contribute to power production, whereas radio waves, microwaves, and most infrared photons will not.[10] This places an immediate limit on the amount of energy that can be extracted from the sun. Of the 1,000 W/m2 in AM1.5 sunlight, about 19% of that has less than 1.1 eV of energy, and will not produce power in a silicon cell.
Another important contributor to losses is that any energy above and beyond the bandgap energy is lost. While blue light has roughly twice the energy of red light, that energy is not captured by devices with a single p-n junction. The electron is ejected with higher energy when struck by a blue photon, but it loses this extra energy as it travels toward the p-n junction (the energy is converted into heat).[10] This accounts for about 33% of the incident sunlight, meaning that, for silicon, from spectrum losses alone there is a theoretical conversion efficiency limit of about 48%, ignoring all other factors.
There is a trade-off in the selection of a bandgap. If the band gap is large, not as many photons create pairs, whereas if the band gap is small, the electron-hole pairs do not contain as much energy.
Shockley and Queisser call the efficiency factor associated with spectrum losses u, for "ultimate efficiency function". Shockley and Queisser calculated that the best band gap for sunlight happens to be 1.1 eV, the value for silicon, and gives a u of 44%. They used blackbody radiation of 6000K for sunlight, and found that the optimum band gap would then have an energy of 2.2 kTs. (At that value, 22% of the blackbody radiation energy would be below the band gap.) Using a more accurate spectrum may give a slightly different optimum. A blackbody at 6000 K puts out 7348 W per square centimetre, so a value for u of 44% and a value of 5.73×1018 photons per joule (corresponding to a band gap of 1.09 V, the value used by Shockley and Queisser) gives Qs equal to 1.85×1022 photons per second per square centimetre.
Impedance matching
If the resistance of the load is too high, the current will be very low, while if the load resistance is too low, the voltage drop across it will be very low. There is an optimal load resistance that will draw the most power from the solar cell at a given illumination level. Shockley and Queisser call the ratio of power extracted to IshVoc the impedance matching factor, m. (It is also called the fill factor.) The optimum depends on the shape of the I versus V curve. For very low illumination, the curve is more or less a diagonal line, and m will be 1/4. But for high illumination, m approaches 1. Shockley and Queisser give a graph showing m as a function of the ratio zoc of the open-circuit voltage to the thermal voltage Vc. According to the authors, this ratio is well approximated by ln(fQs/Qc), where f is the combination of factors fsfωts/(2tc), in which fω is the solid angle of the sun divided by π. The maximum value of f without light concentration (with reflectors for example) is just fω/2, or 1.09×10−5, according to the authors. Using the above-mentioned values of Qs and Qc, this gives a ratio of open-circuit voltage to thermal voltage of 32.4 (Voc equal to 77% of the band gap). The authors derive the equation
which can be solved to find zm, the ratio of optimal voltage to thermal voltage. For a zoc of 32.4, we find zm equal to 29.0. One can then use the formula
to find the impedance matching factor. For a zoc of 32.4, this comes to 86.5%.
All together
Considering the spectrum losses alone, a solar cell has a peak theoretical efficiency of 48% (or 44% according to Shockley and Queisser – their "ultimate efficiency factor"). Thus the spectrum losses represent the vast majority of lost power. Including the effects of recombination and the I versus V curve, the efficiency is described by the following equation:
with
where u, v, and m are respectively the ultimate efficiency factor, the ratio of open-circuit voltage Vop to band-gap voltage Vg, and the impedance matching factor (all discussed above), and Vc is the thermal voltage, and Vs is the voltage equivalent of the temperature of the Sun. Letting ts be 1, and using the values mentioned above of 44%, 77%, and 86.5% for the three factors gives about 29% overall efficiency. Shockley and Queisser say 30% in their abstract, but do not give a detailed calculation. A more recent reference gives, for a single-junction cell, a theoretical peak performance of about 33.7%, or about 337 W/m2 in AM1.5.[1][10]
When the amount of sunlight is increased using reflectors or lenses, the factor fω (and therefore f) will be higher. This raises both v and m. Shockley and Queisser include a graph showing the overall efficiency as a function of band gap for various values of f. For a value of 1, the graph shows a maximum efficiency of just over 40%, getting close to the ultimate efficiency (by their calculation) of 44%.
Other considerations
Shockley and Queisser's work considered the most basic physics only; there are a number of other factors that further reduce the theoretical power.
Limited mobility
When an electron is ejected through photoexcitation, the atom it was formerly bound to is left with a net positive charge. Under normal conditions, the atom will pull off an electron from a surrounding atom in order to neutralize itself. That atom will then attempt to remove an electron from another atom, and so forth, producing an ionization chain reaction that moves through the cell. Since these can be viewed as the motion of a positive charge, it is useful to refer to them as "holes", a sort of virtual positive electron.
Like electrons, holes move around the material, and will be attracted towards a source of electrons. Normally these are provided through an electrode on the back surface of the cell. Meanwhile, the conduction-band electrons are moving forward towards the electrodes on the front surface. For a variety of reasons, holes in silicon move much more slowly than electrons. This means that during the finite time while the electron is moving forward towards the p-n junction, it may meet a slowly moving hole left behind by a previous photoexcitation. When this occurs, the electron recombines at that atom, and the energy is lost (normally through the emission of a photon of that energy, but there are a variety of possible processes).
Recombination places an upper limit on the rate of production; past a certain rate there are so many holes in motion that new electrons will never make it to the p-n junction. In silicon this reduces the theoretical performance under normal operating conditions by another 10% over and above the thermal losses noted above. Materials with higher electron (or hole) mobility can improve on silicon's performance; gallium arsenide (GaAs) cells gain about 5% in real-world examples due to this effect alone. In brighter light, when it is concentrated by mirrors or lenses for example, this effect is magnified. Normal silicon cells quickly saturate, while GaAs continue to improve at concentrations as high as 1500 times.
Non-radiative recombination
Recombination between electrons and holes is detrimental in a solar cell, so designers try to minimize it. However, radiative recombination—when an electron and hole recombine to create a photon that exits the cell into the air—is inevitable, because it is the time-reversed process of light absorption. Therefore, the Shockley–Queisser calculation takes radiative recombination into account; but it assumes (optimistically) that there is no other source of recombination. More realistic limits, which are lower than the Shockley–Queisser limit, can be calculated by taking into account other causes of recombination. These include recombination at defects and grain boundaries.
In crystalline silicon, even if there are no crystalline defects, there is still Auger recombination, which occurs much more often than radiative recombination. By taking this into account, the theoretical efficiency of crystalline silicon solar cells was calculated to be 29.4%.[11]
Frequency-dependent absorption
The frequency dependence of the absorption and effectively the reflectance of materials can be taken into account when calculating the solar cell efficiency.[12][13] According to Shockley-Quiesser limit, solar cell efficiency of semiconductors depend on the band gap of the material. Here, it is assumed that optical absorption starts above the band gap of the material. However, due to finite temperature, optical excitations are possible below the optical gap. We can clearly see this from the tail of the imaginary dielectric function below the optical gap depending on temperature.[14] Since imaginary dielectric functions is, even though low, non-zero below the optical gap, there is absorption of light below the optical gap. For thick enough materials this can cause significant absorption. In the Shockley-Quiesser limit, 100% light absorption is assumed above the band gap of the material in order to find highest possible efficiency of a solar cell in case reflectance is reduced to zero for example by using an anti-reflecting coating. However, the problem with this assumption is that absorbance below the band gap of the material at finite temperatures is neglected which can effect the efficiency. With the inclusion of the absorption below the band gap, the lower limit of the short-circuit current integral is changed from band gap to zero and therefore the equation is defined as;
where Jsc is the short-circuit current, A is the thickness dependent absorbance of the material, Jph is the AM1.5 solar energy flux, and ω is the frequency of light.
Exceeding the limit

It is important to note that the analysis of Shockley and Queisser was based on the following assumptions:
- One electron–hole pair excited per incoming photon
- Thermal relaxation of the electron–hole pair energy in excess of the band gap
- Illumination with non-concentrated sunlight
None of these assumptions is necessarily true, and a number of different approaches have been used to significantly surpass the basic limit.
Multijunction cells
The most widely explored path to higher efficiency solar cells has been multijunction photovoltaic cells, also known as "tandem cells". These cells use multiple p-n junctions, each one tuned to a particular frequency of the spectrum. This reduces the problem discussed above, that a material with a single given bandgap cannot absorb sunlight below the bandgap, and cannot take full advantage of sunlight far above the bandgap. In the most common design, a high-bandgap solar cell sits on top, absorbing high-energy, shorter-wavelength light, and transmitting the rest. Beneath it is a lower-bandgap solar cell which absorbs some of the lower-energy, longer-wavelength light. There may be yet another cell beneath that one, with as many as four layers in total.
The calculation of the fundamental efficiency limits of these multijunction cells works in a fashion similar to those for single-junction cells, with the caveat that some of the light will be converted to other frequencies and re-emitted within the structure. Using methods similar to the original Shockley–Queisser analysis with these considerations in mind produces similar results; a two-layer cell can reach 42% efficiency, three-layer cells 49%, and a theoretical infinity-layer cell 86% in non-concentrated sunlight.[5]
The majority of tandem cells that have been produced to date use three layers, tuned to blue (on top), yellow (middle) and red (bottom). These cells require the use of semiconductors that can be tuned to specific frequencies, which has led to most of them being made of gallium arsenide (GaAs) compounds, often germanium for red, GaAs for yellow, and GaInP2 for blue. They are very expensive to produce, using techniques similar to microprocessor construction but with "chip" sizes on the scale of several centimeters. In cases where outright performance is the only consideration, these cells have become common; they are widely used in satellite applications for instance, where the power-to-weight ratio overwhelms practically every other consideration. They also can be used in concentrated photovoltaic applications (see below), where a relatively small solar cell can serve a large area.
Tandem cells are not restricted to high-performance applications; they are also used to make moderate-efficiency photovoltaics out of cheap but low-efficiency materials. One example is amorphous silicon solar cells, where triple-junction tandem cells are commercially available from Uni-Solar and other companies.
Light concentration
Sunlight can be concentrated with lenses or mirrors to much higher intensity. The sunlight intensity is a parameter in the Shockley–Queisser calculation, and with more concentration, the theoretical efficiency limit increases somewhat. If, however, the intense light heats up the cell, which often occurs in practice, the theoretical efficiency limit may go down all things considered.
In practice, the choice of whether or not to use light concentration is based primarily on other factors besides the small change in solar cell efficiency. These factors include the relative cost per area of solar cells versus focusing optics like lenses or mirrors, the cost of sunlight-tracking systems, the proportion of light successfully focused onto the solar cell, and so on.
A wide variety of optical systems can be used to concentrate sunlight, including ordinary lenses and curved mirrors, fresnel lenses, arrays of small flat mirrors, and luminescent solar concentrators.[15][16] Another proposal suggests spreading out an array of microscopic solar cells on a surface, and focusing light onto them via microlens arrays,[17] while yet another proposal suggests designing a semiconductor nanowire array in such a way that light is concentrated in the nanowires.[18]
Intermediate band photovoltaics
There has been some work on producing mid-energy states within single crystal structures. These cells would combine some of the advantages of the multi-junction cell with the simplicity of existing silicon designs. A detailed limit calculation for these cells with infinite bands suggests a maximum efficiency of 77.2%[19] To date, no commercial cell using this technique has been produced.
Photon upconversion
As discussed above, photons with energy below the bandgap are wasted in ordinary single-junction solar cells. One way to reduce this waste is to use photon upconversion, i.e. incorporating into the module a molecule or material that can absorb two or more below-bandgap photons and then emit one above-bandgap photon. Another possibility is to use two-photon absorption, but this can only work at extremely high light concentration.[20]
Thermal photon upconversion
Thermal upconversion is based on the absorption of photons with low energies in the upconverter, which heats up and re-emits photons with higher energies.[21] The upconversion efficiency can be improved by controlling the optical density of states of the absorber[22] and also by tuning the angularly-selective emission characteristics. For example, a planar thermal upconverting platform can have a front surface that absorbs low-energy photons incident within a narrow angular range, and a back surface that efficiently emits only high-energy photons.[23] A hybrid thermophotovoltaic platform exploiting thermal upconversion was theoretically predicted to demonstrate maximum conversion efficiency of 73% under illumination by non-concentrated sunlight. A detailed analysis of non-ideal hybrid platforms that allows for up to 15% of absorption/re-emission losses yielded limiting efficiency value of 45% for Si PV cells.
Hot electron capture
One of the main loss mechanisms is due to the loss of excess carrier energy above the bandgap. It should be no surprise that there has been a considerable amount of research into ways to capture the energy of the carriers before they can lose it in the crystal structure.[24] One system under investigation for this is quantum dots.[25]
Multiple exciton generation
A related concept is to use semiconductors that generate more than one excited electron per absorbed photon, instead of a single electron at the band edge. Quantum dots have been extensively investigated for this effect, and they have been shown to work for solar-relevant wavelengths in prototype solar cells.[25][26]
Another, more straightforward way to utilise multiple exciton generation is a process called singlet fission (or singlet exciton fission) by which a singlet exciton is converted into two triplet excitons of lower energy. This allows for higher theoretical efficiencies when coupled to a low bandgap semiconductor[27] and quantum efficiencies exceeding 100% have been reported.[28]
Also in materials where the (excited) electrons interact strongly with the remaining electrons such as Mott insulators multiple excitons can be generated.[29]
Fluorescent downconversion/downshifting
Another possibility for increased efficiency is to convert the frequency of light down towards the bandgap energy with a fluorescent material. In particular, to exceed the Shockley–Queisser limit, it is necessary for the fluorescent material to convert a single high-energy photon into several lower-energy ones (quantum efficiency > 1). For example, one photon with more than double the bandgap energy can become two photons above the bandgap energy. In practice, however, this conversion process tends to be relatively inefficient. If a very efficient system were found, such a material could be painted on the front surface of an otherwise standard cell, boosting its efficiency for little cost.[30] In contrast, considerable progress has been made in the exploration of fluorescent downshifting, which converts high-energy light (e. g., UV light) to low-energy light (e. g., red light) with a quantum efficiency smaller than 1. The cell may be more sensitive to these lower-energy photons. Dyes, rare-earth phosphors and quantum dots are actively investigated for fluorescent downshifting.[31] For example, silicon quantum dots enabled downshifting has led to the efficiency enhancement of the state-of-the-art silicon solar cells.[32]
Thermophotovoltaic downconversion
Thermophotovoltaic cells are similar to phosphorescent systems, but use a plate to act as the downconvertor. Solar energy falling on the plate, typically black-painted metal, is re-emitted as lower-energy IR, which can then be captured in an IR cell. This relies on a practical IR cell being available, but the theoretical conversion efficiency can be calculated. For a converter with a bandgap of 0.92 eV, efficiency is limited to 54% with a single-junction cell, and 85% for concentrated light shining on ideal components with no optical losses and only radiative recombination.[33]
See also
References
- William Shockley; Hans J. Queisser (March 1961). "Detailed Balance Limit of Efficiency of p-n Junction Solar Cells" (PDF). Journal of Applied Physics. 32 (3): 510–519. Bibcode:1961JAP....32..510S. doi:10.1063/1.1736034.
- "Hans Queisser". Computer History Museum. Retrieved 17 January 2017.
- S. Rühle (2016). "Tabulated values of the Shockley–Queisser limit for single junction solar cells". Solar Energy. 130: 139–147. Bibcode:2016SoEn..130..139R. doi:10.1016/j.solener.2016.02.015.
- A. De Vos & H. Pauwels (1981). "On the Thermodynamic Limit of Photovoltaic Energy Conversion". Appl. Phys. 25 (2): 119–125. Bibcode:1981ApPhy..25..119D. doi:10.1007/BF00901283. S2CID 119693148.
- De Vos, A. (1980). "Detailed balance limit of the efficiency of tandem solar cells". Journal of Physics D: Applied Physics. 13 (5): 839–846. Bibcode:1980JPhD...13..839D. doi:10.1088/0022-3727/13/5/018. S2CID 250782402.
- "Photovoltaic Cells (Solar Cells), How They Work". specmat.com. Archived from the original on 18 May 2007. Retrieved 2 May 2007.
- A. De Vos & H. Pauwels (1981). "On the Thermodynamic Limit of Photovoltaic Energy Conversion". Appl. Phys. 25 (2): 119–125. Bibcode:1981ApPhy..25..119D. doi:10.1007/BF00901283. S2CID 119693148.
- W. Ruppel; P. Würfel (1980). "Upper limit for the conversion of solar energy". IEEE Transactions on Electron Devices. 27 (4): 877. Bibcode:1980ITED...27..877R. doi:10.1109/T-ED.1980.19950. S2CID 23600093. This paper finds the same open-circuit voltage and short-circuit current as de Vos and Pauwels, but does not give the correct function for I(V).
- Byrnes, Steven. "The Shockley-Queisser limit". Retrieved 10 March 2016.
- C. S. Solanki and G. Beaucarne, "Advanced Solar Cell Concepts", Interuniversity Microelectronics Center, Belgium
- A. Richter; M. Hermle; S.W. Glunz (October 2013). "Reassessment of the limiting efficiency for crystalline silicon solar cells". IEEE Journal of Photovoltaics. 3 (4): 1184–1191. doi:10.1109/JPHOTOV.2013.2270351. S2CID 6013813.
- B. Ozdemir, V. Barone (2020). "Thickness dependence of solar cell efficiency in transition metal dichalcogenides MX2 (M: Mo, W; X: S, Se, Te)". Solar Energy Materials and Solar Cells. 212: 110557. doi:10.1016/j.solmat.2020.110557. hdl:11693/75812. S2CID 216528272.
- S. Kim, J. A. Márquez, T. Unold, A. Walsh (2020). "Upper limit to the photovoltaic efficiency of imperfect crystals from first principles". Energy & Environmental Science. 13: 1481–1491. doi:10.1039/D0EE00291G. hdl:10044/1/84273.
{{cite journal}}: CS1 maint: multiple names: authors list (link) - P. Lautenschlager, M. Garriga, L. Vina, M. Cardona (1987). "Temperature dependence of the dielectric function and interband critical points in silicon". Phys. Rev. B. 36 (9): 4821–4830. Bibcode:1987PhRvB..36.4821L. doi:10.1103/PhysRevB.36.4821. PMID 9943498.
{{cite journal}}: CS1 maint: multiple names: authors list (link) - Elizabeth A. Thomson, "MIT opens new 'window' on solar energy", MIT News, 10 July 2008
- Kittidachachan, Pattareeya; Danos, Lefteris; Meyer, Thomas J. J.; Alderman, Nicolas; Markvart, Tom (19 December 2007). "Photon Collection Efficiency of Fluorescent Solar Collectors" (PDF). CHIMIA International Journal for Chemistry. 61 (12): 780–786. doi:10.2533/chimia.2007.780.
- "Microsystems Enabled Photovoltaics, Sandia National Laboratories". Archived from the original on 5 April 2013. Retrieved 26 March 2013.
- Krogstrup, Peter; Jørgensen, Henrik Ingerslev; Heiss, Martin; Demichel, Olivier; Holm, Jeppe V.; Aagesen, Martin; Nygard, Jesper; Fontcuberta i Morral, Anna (24 March 2013). "Single-nanowire solar cells beyond the Shockley–Queisser limit". Nature Photonics. 7 (4): 306–310. arXiv:1301.1068. Bibcode:2013NaPho...7..306K. doi:10.1038/nphoton.2013.32. S2CID 6096888.
- Brown, Andrew S.; Green, Martin A. (2002). "Impurity photovoltaic effect: Fundamental energy conversion efficiency limits". Journal of Applied Physics. 92 (3): 1329. Bibcode:2002JAP....92.1329B. doi:10.1063/1.1492016.
- Jalali, Bahram; Fathpour, Sasan; Tsia, Kevin (2009). "Green Silicon Photonics". Optics and Photonics News. 20 (6): 18. doi:10.1364/OPN.20.6.000018. hdl:10722/124710.
- Ekins-Daukes, N. J. (2003). "Photovoltaic efficiency enhancement through thermal up-conversion". Applied Physics Letters. 82 (12): 1974. Bibcode:2003ApPhL..82.1974E. doi:10.1063/1.1561159. S2CID 117441695.
- Farrell, D. J. (2011). "A hot-carrier solar cell with optical energy selective contacts". Applied Physics Letters. 99 (11): 111102. Bibcode:2011ApPhL..99k1102F. doi:10.1063/1.3636401.
- Boriskina, Svetlana V. (2014). "Exceeding the solar cell Shockley–Queisser limit via thermal up-conversion of low-energy photons". Optics Communications. 314: 71–78. arXiv:1310.5570. Bibcode:2014OptCo.314...71B. doi:10.1016/j.optcom.2013.10.042. hdl:1721.1/110465. S2CID 33141699.
- Gavin Conibeer et al., "Hot Carrier Solar Cell: Implementation of the Ultimate Photovoltaic Converter", Global Climate & Energy Project, Stanford University, September 2008
- A. J. Nozik, "Quantum Dot Solar Cells", National Renewable Energy Laboratory, October 2001
- Semonin, O. E. (2011). "Peak External Photocurrent Quantum Efficiency Exceeding 100% via MEG in a Quantum Dot Solar Cell". Science. 334 (6062): 1530–1533. Bibcode:2011Sci...334.1530S. doi:10.1126/science.1209845. PMID 22174246. S2CID 36022754.
- Ehrler, B. (2012). "Singlet Exciton Fission-Sensitized Infrared Quantum Dot Solar Cells". Nano Letters. 12 (2): 1053–1057. Bibcode:2012NanoL..12.1053E. doi:10.1021/nl204297u. PMID 22257168.
- Congreve, D. N. (2013). "External Quantum Efficiency Above 100% in a Singlet-Exciton-Fission–Based Organic Photovoltaic Cell". Science. 340 (6130): 334–337. Bibcode:2013Sci...340..334C. doi:10.1126/science.1232994. PMID 23599489. S2CID 46185590.
- P. Werner; K. Held & M. Eckstein (2014). "Role of impact ionization in the thermalization of photoexcited Mott insulators". Phys. Rev. B. 90 (23): 235102. arXiv:1408.3425. Bibcode:2014PhRvB..90w5102W. doi:10.1103/PhysRevB.90.235102. S2CID 53387271.
- "Sunovia, EPIR Demonstrate Optical Down-Conversion For Solar Cells"
- Klampaftis, Efthymios; Ross, David; McIntosh, Keith R.; Richards, Bryce S. (August 2009). "Enhancing the performance of solar cells via luminescent down-shifting of the incident spectrum: A review". Solar Energy Materials and Solar Cells. 93 (8): 1182–1194. doi:10.1016/j.solmat.2009.02.020.
- Pi, Xiaodong; Zhang, Li; Yang, Deren (11 October 2012). "Enhancing the Efficiency of Multicrystalline Silicon Solar Cells by the Inkjet Printing of Silicon-Quantum-Dot Ink". The Journal of Physical Chemistry C. 116 (40): 21240–21243. doi:10.1021/jp307078g.
- Harder, Nils-Peter; Würfel, Peter (2003). "Theoretical limits of thermophotovoltaic solar energy conversion". Semiconductor Science and Technology. 18 (5): S151–S157. Bibcode:2003SeScT..18S.151H. doi:10.1088/0268-1242/18/5/303. S2CID 250841378.
External links
- Reproduction of the Shockley–Queisser calculation (PDF), using the Mathematica software program. This code was used to calculate all the graphs in this article.
- Luque, Antonio, and Antonio Martí. "Chapter 4: Theoretical Limits of Photovoltaic Conversion and New-generation Solar Cells." Ed. Antonio Luque and Steven Hegedus. Handbook of Photovoltaic Science and Engineering. Second ed. N.p.: John Wiley & Sons, 2011. 130–68. Print.