Link (simplicial complex)

Given an abstract simplicial complex X and ${\textstyle v}$ a vertex in ${\textstyle V(X)}$, its link ${\textstyle \operatorname {Lk} (v,X)}$ is a set containing every face ${\textstyle \tau \in X}$ such that ${\textstyle v\not \in \tau }$ and ${\textstyle \tau \cup \{v\}}$ is a face of X.

• In the special case in which X is a 1-dimensional complex (that is: a graph), ${\textstyle \operatorname {Lk} (v,X)}$ contains all vertices ${\textstyle u\neq v}$ such that ${\textstyle \{u,v\}}$ is an edge in the graph; that is, ${\textstyle \operatorname {Lk} (v,X)={\mathcal {N}}(v)=}$the neighborhood of ${\textstyle v}$ in the graph.

Given a geometric simplicial complex X and ${\textstyle v\in V(X)}$, its link ${\textstyle \operatorname {Lk} (v,X)}$ is a set containing every face ${\textstyle \tau \in X}$ such that ${\textstyle v\not \in \tau }$ and there is a simplex in ${\textstyle X}$ that has ${\textstyle v}$ as a vertex and ${\textstyle \tau }$ as a face.[1]^: 3 Equivalently, the join ${\textstyle v\star \tau }$ is a face in ${\textstyle X}$.[2]^: 20

• As an example, suppose v is the top vertex of the tetrahedron at the left. Then the link of v is the triangle at the base of the tetrahedron. This is because, for each edge of that triangle, the join of v with the edge is a triangle (one of the three triangles at the sides of the tetrahedron); and the join of v with the triangle itself is the entire tetrahedron.
  

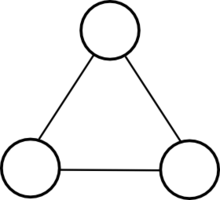  The link of a vertex of a tetrahedron is the triangle.

An alternative definition is: the link of a vertex ${\textstyle v\in V(X)}$ is the graph Lk(v, X) constructed as follows. The vertices of Lk(v, X) are the edges of X incident to v. Two such edges are adjacent in Lk(v, X) iff they are incident to a common 2-cell at v.

• The graph Lk(v, X) is often given the topology of a ball of small radius centred at v; it is an analog to a sphere centered at a point.[3]

The definition of a link can be extended from a single vertex to any face.

Given an abstract simplicial complex X and any face ${\textstyle \sigma }$ of X, its link ${\textstyle \operatorname {Lk} (\sigma ,X)}$ is a set containing every face ${\textstyle \tau \in X}$ such that ${\textstyle \sigma ,\tau }$ are disjoint and ${\textstyle \tau \cup \sigma }$ is a face of X: ${\textstyle \operatorname {Lk} (\sigma ,X):=\{\tau \in X:~\tau \cap \sigma =\emptyset ,~\tau \cup \sigma \in X\}}$.

Given a geometric simplicial complex X and any face ${\textstyle \sigma \in X}$, its link ${\textstyle \operatorname {Lk} (\sigma ,X)}$ is a set containing every face ${\textstyle \tau \in X}$ such that ${\textstyle \sigma ,\tau }$ are disjoint and there is a simplex in ${\textstyle X}$ that has both ${\textstyle \sigma }$ and ${\textstyle \tau }$ as faces.[1]^: 3

The link of a vertex of a tetrahedron is a triangle – the three vertices of the link corresponds to the three edges incident to the vertex, and the three edges of the link correspond to the faces incident to the vertex. In this example, the link can be visualized by cutting off the vertex with a plane; formally, intersecting the tetrahedron with a plane near the vertex – the resulting cross-section is the link.

Another example is illustrated below. There is a two-dimensional simplicial complex. At the left, a vertex is marked in yellow. At the right, the link of that vertex is marked in green.

• 
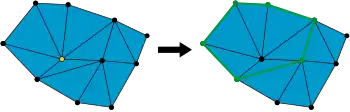  A vertex and its link.

• For any simplicial complex X, every link ${\textstyle \operatorname {Lk} (\sigma ,X)}$ is downward-closed, and therefore it is a simplicial complex too; it is a sub-complex of X.
• Because X is simplicial, there is a set isomorphism between ${\textstyle \operatorname {Lk} (\sigma ,X)}$ and the set ${\displaystyle X_{\sigma }:=\{\rho \in X{\text{ such that }}\sigma \subseteq \rho \}}$: every ${\textstyle \tau \in \operatorname {Lk} (\sigma ,X)}$ corresponds to ${\textstyle \tau \cup \sigma }$, which is in ${\displaystyle X_{\sigma }}$.

A concept closely related to the link is the star.

Given an abstract simplicial complex X and any face ${\textstyle \sigma \in X}$,${\textstyle V(X)}$, its star ${\textstyle \operatorname {St} (\sigma ,X)}$ is a set containing every face ${\textstyle \tau \in X}$ such that ${\textstyle \tau \cup \sigma }$ is a face of X. In the special case in which X is a 1-dimensional complex (that is: a graph), ${\textstyle \operatorname {St} (v,X)}$ contains all edges ${\textstyle \{u,v\}}$ for all vertices ${\textstyle u}$ that are neighbors of ${\textstyle v}$. That is, it is a graph-theoretic star centered at ${\textstyle u}$.

Given a geometric simplicial complex X and any face Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "http://localhost:6011/en.wikipedia.org/v1/":): {\textstyle \sigma \in X} , its star ${\textstyle \operatorname {St} (\sigma ,X)}$ is a set containing every face ${\textstyle \tau \in X}$ such that there is a simplex in ${\textstyle X}$ having both ${\textstyle \sigma }$ and ${\textstyle \tau }$ as faces: ${\textstyle \operatorname {St} (\sigma ,X):=\{\tau \in X:\exists \rho \in X:\tau ,\sigma {\text{ are faces of }}\rho \}}$. In other words, it is the closure of the set ${\textstyle \{\rho \in X:\sigma {\text{ is a face of }}\rho \}}$ -- the set of simplices having ${\textstyle \sigma }$ as a face.

So the link is a subset of the star. The star and link are related as follows:

• For any ${\textstyle \sigma \in X}$, ${\textstyle \operatorname {Lk} (\sigma ,X)=\{\tau \in \operatorname {St} (\sigma ,X):\tau \cap \sigma =\emptyset \}}$. [1]^: 3
• For any ${\textstyle v\in V(X)}$, ${\textstyle \operatorname {St} (v,X)=v\star \operatorname {Lk} (v,X)}$, that is, the star of ${\textstyle v}$ is the cone of its link at ${\textstyle v}$.[2]^: 20

An example is illustrated below. There is a two-dimensional simplicial complex. At the left, a vertex is marked in yellow. At the right, the star of that vertex is marked in green.

• 
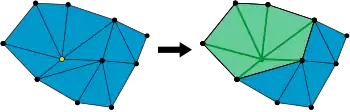  A vertex and its star.

• Vertex figure - a geometric concept similar to the simplicial link.