Cage effect

In chemistry, the cage effect[1] (also known as geminate recombination[2]) describes how the properties of a molecule are affected by its surroundings. First introduced by James Franck and Eugene Rabinowitch[3][4] in 1934, the cage effect suggests that instead of acting as an individual particle, molecules in solvent are more accurately described as an encapsulated particle. The encapsulated molecules or radicals are called cage pairs or geminate pairs.[5][6] In order to interact with other molecules, the caged particle must diffuse from its solvent cage. The typical lifetime of a solvent cage is 10^-11 seconds.[7] Many manifestations of the cage effect exist.[8]

Free radicals in solvent can potentially react with a monomer within the solvent cage or diffuse out.

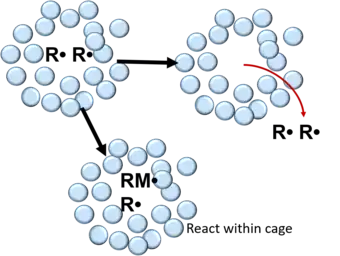
In free radical polymerization, radicals formed from the decomposition of an initiator molecule are surrounded by a cage consisting of solvent and/or monomer molecules.[6] Within the cage, the free radicals undergo many collisions leading to their recombination or mutual deactivation.[5][6][9] This can be described by the following reaction:

${\displaystyle R\!-\!R\;\;{\underset {k_{c}}{\overset {k_{1}}{\rightleftharpoons }}}\;\;{\underset {\text{cage pair}}{(R^{\,\bullet },^{\bullet }\!R)}}\;\;{\underset {k_{D}}{\overset {k_{d}}{\rightleftharpoons }}}\;\;{\underset {\text{free radicals}}{2R^{\,\bullet }}}\;\rightarrow \;{\text{Products}}}$[9]

After recombination, free radicals can either react with monomer molecules within the cage walls or diffuse out of the cage. In polymers, the probability of a free radical pair to escape recombination in the cage is 0.1 – 0.01 and 0.3-0.8 in liquids.[5] In unimolecular chemistry, geminate recombination has first been studied in the solution phase using iodine molecules[10] and heme proteins.[11][12] In the solid state, geminate recombination has been demonstrated with small molecules trapped in noble gas solid matrices[13] and in triiodide crystalline compounds.[14][15][16]