Sparse ruler
A sparse ruler is a ruler in which some of the distance marks may be missing. More abstractly, a sparse ruler of length with marks is a sequence of integers where . The marks and correspond to the ends of the ruler. In order to measure the distance , with there must be marks and such that .
A complete sparse ruler allows one to measure any integer distance up to its full length. A complete sparse ruler is called minimal if there is no complete sparse ruler of length with marks. In other words, if any of the marks is removed one can no longer measure all of the distances, even if the marks could be rearranged. A complete sparse ruler is called maximal if there is no complete sparse ruler of length with marks. A sparse ruler is called optimal if it is both minimal and maximal.
Since the number of distinct pairs of marks is , this is an upper bound on the length of any maximal sparse ruler with marks. This upper bound can be achieved only for 2, 3 or 4 marks. For larger numbers of marks, the difference between the optimal length and the bound grows gradually, and unevenly.
For example, for 6 marks the upper bound is 15, but the maximal length is 13. There are 3 different configurations of sparse rulers of length 13 with 6 marks. One is {0, 1, 2, 6, 10, 13}. To measure a length of 7, say, with this ruler one would take the distance between the marks at 6 and 13.
A Golomb ruler is a sparse ruler that requires all of the differences be distinct. In general, a Golomb ruler with marks will be considerably longer than an optimal sparse ruler with marks, since is a lower bound for the length of a Golomb ruler. A long Golomb ruler will have gaps, that is, it will have distances which it cannot measure. For example, the optimal Golomb ruler {0, 1, 4, 10, 12, 17} has length 17, but cannot measure lengths of 14 or 15.
Wichmann rulers
Many optimal rulers are of the form where represents segments of length . Thus, if and , then has (in order):
1 segment of length 1,
1 segment of length 2,
1 segment of length 3,
2 segments of length 7,
2 segments of length 4,
1 segment of length 1
That gives the ruler {0, 1, 3, 6, 13, 20, 24, 28, 29}. The length of a Wichmann ruler is and the number of marks is . Note that not all Wichmann rulers are optimal and not all optimal rulers can be generated this way. None of the optimal rulers of length 1, 13, 17, 23 and 58 follow this pattern. That sequence ends with 58 if the Optimal Ruler Conjecture of Peter Luschny is correct. The conjecture is known to be true to length 213.[1]
Asymptotics
For every let be the smallest number of marks for a ruler of length . For example, . The asymptotic of the function was studied by Erdos, Gal[2] (1948) and continued by Leech[3] (1956) who proved that the limit exists and is lower and upper bounded by
Much better upper bounds exist for -perfect rulers. Those are subsets of such that each positive number can be written as a difference for some . For every number let be the smallest cardinality of an -perfect ruler. It is clear that . The asymptotics of the sequence was studied by Redei, Renyi[4] (1949) and then by Leech (1956) and Golay[5] (1972). Due to their efforts the following upper and lower bounds were obtained:
Define the excess as . In 2020, Pegg proved by construction that ≤ 1 for all lengths .[6] If the Optimal Ruler Conjecture is true, then for all , leading to the ″dark mills″ pattern when arranged in columns, OEIS A326499.[7] None of the best known sparse rulers are proven minimal as of Sep 2020. Many of the current best known constructions for are believed to non-minimal, especially the "cloud" values.
 Fig 1. Light numbers +0, dark numbers +1 for the minimal mark excess pattern in a sparse ruler. All minimal values to length 213 are proven.
Fig 1. Light numbers +0, dark numbers +1 for the minimal mark excess pattern in a sparse ruler. All minimal values to length 213 are proven.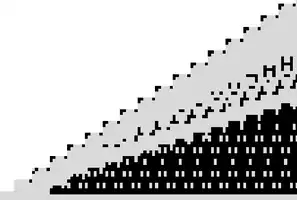 Fig 2. "Dark mills on a cloudy day" -- N. J. A. Sloane. Excess pattern for sparse rulers, best known values for L>213.
Fig 2. "Dark mills on a cloudy day" -- N. J. A. Sloane. Excess pattern for sparse rulers, best known values for L>213.
Examples
The following are examples of minimal sparse rulers. Optimal rulers are highlighted. When there are too many to list, not all are included. Mirror images are not shown.
| Length | Marks | Number | Examples | List Form | Wichmann |
|---|---|---|---|---|---|
| 1 | 2 | 1 | II | {0, 1} | |
| 2 | 3 | 1 | III | {0, 1, 2} | |
| 3 | 3 | 1 | II.I | {0, 1, 3} | W(0,0) |
| 4 | 4 | 2 | III.I II.II | {0, 1, 2, 4} {0, 1, 3, 4} | |
| 5 | 4 | 2 | III..I II.I.I | {0, 1, 2, 5} {0, 1, 3, 5} | |
| 6 | 4 | 1 | II..I.I | {0, 1, 4, 6} | W(0,1) |
| 7 | 5 | 6 | IIII...I III.I..I III..I.I II.I.I.I II.I..II II..II.I | {0, 1, 2, 3, 7} {0, 1, 2, 4, 7} {0, 1, 2, 5, 7} {0, 1, 3, 5, 7} {0, 1, 3, 6, 7} {0, 1, 4, 5, 7} | |
| 8 | 5 | 4 | III..I..I II.I...II II..I.I.I II...II.I | {0, 1, 2, 5, 8} {0, 1, 3, 7, 8} {0, 1, 4, 6, 8} {0, 1, 5, 6, 8} | |
| 9 | 5 | 2 | III...I..I II..I..I.I | {0, 1, 2, 6, 9} {0, 1, 4, 7, 9} | - W(0,2) |
| 10 | 6 | 19 | IIII..I...I | {0, 1, 2, 3, 6, 10} | |
| 11 | 6 | 15 | IIII...I...I | {0, 1, 2, 3, 7, 11} | |
| 12 | 6 | 7 | IIII....I...I III...I..I..I II.I.I.....II II.I...I...II II..II....I.I II..I..I..I.I II.....II.I.I | {0, 1, 2, 3, 8, 12} {0, 1, 2, 6, 9, 12} {0, 1, 3, 5, 11, 12} {0, 1, 3, 7, 11, 12} {0, 1, 4, 5, 10, 12} {0, 1, 4, 7, 10, 12} {0, 1, 7, 8, 10, 12} | - - - - - W(0,3) - |
| 13 | 6 | 3 | III...I...I..I II..II.....I.I II....I..I.I.I | {0, 1, 2, 6, 10, 13} {0, 1, 4, 5, 11, 13} {0, 1, 6, 9, 11, 13} | |
| 14 | 7 | 65 | IIIII....I....I | {0, 1, 2, 3, 4, 9, 14} | |
| 15 | 7 | 40 | II.I..I...I...II II..I..I..I..I.I | {0, 1, 3, 6, 10, 14, 15} {0, 1, 4, 7, 10, 13, 15} | W(1,0) W(0,4) |
| 16 | 7 | 16 | IIII....I...I...I | {0, 1, 2, 3, 8, 12, 16} | |
| 17 | 7 | 6 | IIII....I....I...I III...I...I...I..I III.....I...I.I..I III.....I...I..I.I II..I.....I.I..I.I II......I..I.I.I.I | {0, 1, 2, 3, 8, 13, 17} {0, 1, 2, 6, 10, 14, 17} {0, 1, 2, 8, 12, 14, 17} {0, 1, 2, 8, 12, 15, 17} {0, 1, 4, 10, 12, 15, 17} {0, 1, 8, 11, 13, 15, 17} | |
| 18 | 8 | 250 | II..I..I..I..I..I.I | {0, 1, 4, 7, 10, 13, 16, 18} | W(0,5) |
| 19 | 8 | 163 | IIIII....I....I....I | {0, 1, 2, 3, 4, 9, 14, 19} | |
| 20 | 8 | 75 | IIIII.....I....I....I | {0, 1, 2, 3, 4, 10, 15, 20} | |
| 21 | 8 | 33 | IIIII.....I.....I....I | {0, 1, 2, 3, 4, 10, 16, 21} | |
| 22 | 8 | 9 | IIII....I....I....I...I III.......I....I..I..II II.I.I........II.....II II.I..I......I...I...II II.I.....I.....I...II.I II..II......I.I.....I.I II....II..I.......I.I.I II....I..I......I.I.I.I II.....II........II.I.I | {0, 1, 2, 3, 8, 13, 18, 22} {0, 1, 2, 10, 15, 18, 21, 22} {0, 1, 3, 5, 14, 15, 21, 22} {0, 1, 3, 6, 13, 17, 21, 22} {0, 1, 3, 9, 15, 19, 20, 22} {0, 1, 4, 5, 12, 14, 20, 22} {0, 1, 6, 7, 10, 18, 20, 22} {0, 1, 6, 9, 16, 18, 20, 22} {0, 1, 7, 8, 17, 18, 20, 22} | - - - W(1,1) - - - - - |
| 23 | 8 | 2 | III........I...I..I..I.I II..I.....I.....I.I..I.I | {0, 1, 2, 11, 15, 18, 21, 23} {0, 1, 4, 10, 16, 18, 21, 23} | |
| 24 | 9 | 472 | IIIIII......I.....I.....I | {0, 1, 2, 3, 4, 5, 12, 18, 24} | |
| 25 | 9 | 230 | IIIIII......I......I.....I | {0, 1, 2, 3, 4, 5, 12, 19, 25} | |
| 26 | 9 | 83 | IIIII.....I....I.....I....I | {0, 1, 2, 3, 4, 10, 15, 21, 26} | |
| 27 | 9 | 28 | IIIII.....I.....I.....I....I | {0, 1, 2, 3, 4, 10, 16, 22, 27} | |
| 28 | 9 | 6 | III..........I....I..I..I..II II.I.I.I..........II.......II II.I..I..I......I......I...II II.I.....I.....I.....I...II.I II.....I...I........I..I.II.I II.......II..........II.I.I.I | {0, 1, 2, 13, 18, 21, 24, 27, 28} {0, 1, 3, 5, 7, 18, 19, 27, 28} {0, 1, 3, 6, 9, 16, 23, 27, 28} {0, 1, 3, 9, 15, 21, 25, 26, 28} {0, 1, 7, 11, 20, 23, 25, 26, 28} {0, 1, 9, 10, 21, 22, 24, 26, 28} | |
| 29 | 9 | 3 | III...........I...I..I..I..I.I II.I..I......I......I...I...II II..I.....I.....I.....I.I..I.I | {0, 1, 2, 14, 18, 21, 24, 27, 29} {0, 1, 3, 6, 13, 20, 24, 28, 29} {0, 1, 4, 10, 16, 22, 24, 27, 29} | - W(1,2) - |
| 35 | 10 | 5 | III..............I...I..I..I..I..I.I II.I..I..I......I......I......I...II II.I..I..I.........I...I......I...II II..II..........I.I......I.I.....I.I II..I.....I.....I.....I.....I.I..I.I | {0, 1, 2, 17, 21, 24, 27, 30, 33, 35} {0, 1, 3, 6, 9, 16, 23, 30, 34, 35} {0, 1, 3, 6, 9, 19, 23, 30, 34, 35} {0, 1, 4, 5, 16, 18, 25, 27, 33, 35} {0, 1, 4, 10, 16, 22, 28, 30, 33, 35} | |
| 36 | 10 | 1 | II.I..I......I......I......I...I...II | {0, 1, 3, 6, 13, 20, 27, 31, 35, 36} | W(1,3) |
| 43 | 11 | 1 | II.I..I......I......I......I......I...I...II | {0, 1, 3, 6, 13, 20, 27, 34, 38, 42, 43} | W(1,4) |
| 46 | 12 | 342 | III..I....I....I..........I.....I.....I.....III | {0, 1, 2, 5, 10, 15, 26, 32, 38, 44, 45, 46} | W(2,1) |
| 50 | 12 | 2 | IIII...................I....I...I...I...I...I..I..I II.I..I......I......I......I......I......I...I...II | {0, 1, 2, 3, 23, 28, 32, 36, 40, 44, 47, 50} {0, 1, 3, 6, 13, 20, 27, 34, 41, 45, 49, 50} | - W(1,5) |
| 57 | 13 | 12 | III..I....I....I..........I..........I.....I.....I.....III II.I..I......I......I......I......I......I......I...I...II | {0, 1, 2, 5, 10, 15, 26, 37, 43, 49, 55, 56, 57} {0, 1, 3, 6, 13, 20, 27, 34, 41, 48, 52, 56, 57} | W(2,2) W(1,6) |
| 58 | 13 | 6 | IIII.......................I....I...I...I...I...I...I..I..I III...I.I........I........I........I........I..I......I..II III.....I......II.........I.........I.........I..I...I.I..I II.I..I..........I..I......I.......I.........I...I...I...II II.I..I..........I......I..I..........I......I...I...I...II II...I..I...I........I........I........I........I....II.I.I | {0, 1, 2, 3, 27, 32, 36, 40, 44, 48, 52, 55, 58} {0, 1, 2, 6, 8, 17, 26, 35, 44, 47, 54, 57, 58} {0, 1, 2, 8, 15, 16, 26, 36, 46, 49, 53, 55, 58} {0, 1, 3, 6, 17, 20, 27, 35, 45, 49, 53, 57, 58} {0, 1, 3, 6, 17, 24, 27, 38, 45, 49, 53, 57, 58} {0, 1, 5, 8, 12, 21, 30, 39, 48, 53, 54, 56, 58} | |
| 68 | 14 | 2 | III..I....I....I..........I..........I..........I.....I.....I.....III III.....I......II.........I.........I.........I.........I..I...I.I..I | {0, 1, 2, 5, 10, 15, 26, 37, 48, 54, 60, 66, 67, 68} {0, 1, 2, 8, 15, 16, 26, 36, 46, 56, 59, 63, 65, 68} | W(2,3) - |
| 79 | 15 | 1 | III..I....I....I..........I..........I..........I..........I.....I.....I.....III | {0, 1, 2, 5, 10, 15, 26, 37, 48, 59, 65, 71, 77, 78, 79} | W(2,4) |
| 90 | 16 | 1 | III..I....I....I..........I..........I..........I..........I..........I.....I.....I.....III | {0, 1, 2, 5, 10, 15, 26, 37, 48, 59, 70, 76, 82, 88, 89, 90} | W(2,5) |
| 101 | 17 | 1 | III..I....I....I..........I..........I..........I..........I..........I..........I.....I.....I.....III | {0,1,2,5,10,15,26,37,48,59,70,81,87,93,99,100,101} | W(2,6) |
| 112 | 18 | 1 | III..I....I....I..........I..........I..........I..........I..........I..........I..........I.....I.....I.....III | {0,1,2,5,10,15,26,37,48,59,70,81,92,98,104,110,111,112} | W(2,7) |
| 123 | 19 | 2 | IIII...I......I......I......I..............I..............I..............I..............I.......I.......I.......I.......IIII
III..I....I....I..........I..........I..........I..........I..........I..........I..........I..........I.....I.....I.....III |
{0,1,2,3,7,14,21,28,43,58,73,88,96,104,112,120,121,122,123} {0,1,2,5,10,15,26,37,48,59,70,81,92,103,109,115,121,122,123} | W(3,4) W(2,8) |
| 138 | 20 | 1 | IIII...I......I......I......I..............I..............I..............I..............I..............I.......I.......I.......I.......IIII | {0,1,2,3,7,14,21,28,43,58,73,88,103,111,119,127,135,136,137,138} | W(3,5) |
Incomplete sparse rulers
A few incomplete rulers can fully measure up to a longer distance than an optimal sparse ruler with the same number of marks. , , , and can each measure up to 18, while an optimal sparse ruler with 7 marks can measure only up to 17. The table below lists these rulers, up to rulers with 13 marks. Mirror images are not shown. Rulers that can fully measure up to a longer distance than any shorter ruler with the same number of marks are highlighted.
| Marks | Length | Measures up to | Ruler |
|---|---|---|---|
| 7 | 24 | 18 | {0, 2, 7, 14, 15, 18, 24} |
| 7 | 25 | 18 | {0, 2, 7, 13, 16, 17, 25} |
| 7 | 31 | 18 | {0, 5, 7, 13, 16, 17, 31} |
| 7 | 31 | 18 | {0, 6, 10, 15, 17, 18, 31} |
| 8 | 39 | 24 | {0, 8, 15, 17, 20, 21, 31, 39} |
| 10 | 64 | 37 | {0, 7, 22, 27, 28, 31, 39, 41, 57, 64} |
| 10 | 73 | 37 | {0, 16, 17, 28, 36, 42, 46, 49, 51, 73} |
| 11 | 68 | 44 | {0, 7, 10, 27, 29, 38, 42, 43, 44, 50, 68} |
| 11 | 91 | 45 | {0, 18, 19, 22, 31, 42, 48, 56, 58, 63, 91} |
| 12 | 53 | 51 | {0, 2, 3, 6, 9, 17, 25, 33, 41, 46, 51, 53} |
| 12 | 60 | 51 | {0, 5, 9, 13, 19, 26, 33, 48, 49, 50, 51, 60} |
| 12 | 73 | 51 | {0, 2, 3, 10, 17, 23, 35, 42, 46, 47, 51, 73} |
| 12 | 75 | 51 | {0, 2, 10, 13, 29, 33, 36, 45, 50, 51, 57, 75} |
| 12 | 82 | 51 | {0, 8, 28, 31, 34, 38, 45, 47, 49, 50, 74, 82} |
| 12 | 83 | 51 | {0, 2, 10, 24, 25, 29, 36, 42, 45, 73, 75, 83} |
| 12 | 85 | 51 | {0, 8, 10, 19, 35, 41, 42, 47, 55, 56, 59, 85} |
| 12 | 87 | 51 | {0, 12, 24, 26, 37, 39, 42, 43, 46, 47, 75, 87} |
| 13 | 61 | 59 | {0, 2, 3, 6, 9, 17, 25, 33, 41, 49, 54, 59, 61} |
| 13 | 69 | 59 | {0, 6, 10, 15, 22, 30, 38, 55, 56, 57, 58, 59, 69} |
| 13 | 69 | 59 | {0, 6, 11, 15, 22, 30, 38, 55, 56, 57, 58, 59, 69} |
| 13 | 82 | 59 | {0, 4, 5, 9, 25, 27, 39, 42, 50, 53, 56, 63, 82} |
| 13 | 83 | 59 | {0, 1, 2, 24, 34, 36, 38, 43, 51, 54, 57, 82, 83} |
| 13 | 88 | 59 | {0, 1, 3, 9, 16, 26, 36, 40, 47, 54, 58, 59, 88} |
| 13 | 88 | 59 | {0, 1, 5, 29, 34, 36, 47, 48, 50, 56, 58, 73, 88} |
| 13 | 90 | 59 | {0, 7, 12, 16, 37, 38, 43, 55, 56, 57, 58, 66, 90} |
| 13 | 91 | 59 | {0, 5, 9, 12, 16, 32, 38, 42, 55, 56, 57, 63, 91} |
| 13 | 92 | 59 | {0, 6, 10, 13, 25, 34, 39, 54, 55, 56, 57, 65, 92} |
| 13 | 94 | 59 | {0, 1, 3, 16, 28, 37, 45, 48, 54, 55, 59, 78, 94} |
| 13 | 95 | 59 | {0, 4, 32, 37, 38, 40, 48, 53, 54, 56, 63, 83, 95} |
| 13 | 96 | 59 | {0, 3, 7, 27, 37, 39, 50, 55, 56, 58, 72, 81, 96} |
| 13 | 101 | 59 | {0, 4, 24, 37, 43, 45, 52, 54, 55, 59, 77, 81, 101} |
| 13 | 108 | 59 | {0, 8, 17, 40, 50, 53, 64, 65, 69, 71, 91, 99, 108} |
| 13 | 113 | 61 | {0, 6, 22, 36, 45, 47, 57, 60, 64, 65, 91, 97, 113} |
| 13 | 133 | 60 | {0, 26, 29, 40, 42, 46, 67, 74, 79, 89, 97, 98, 133} |
See also
References
- Robison, A. D. Parallel Computation of Sparse Rulers. Intel Developer Zone. https://web.archive.org/web/20210330141047/https://software.intel.com/content/www/us/en/develop/articles/parallel-computation-of-sparse-rulers.html
- Erdös, P.; Gál, I. S. On the representation of by differences. Nederl. Akad. Wetensch., Proc. 51 (1948) 1155--1158 = Indagationes Math. 10, 379--382 (1949)
- Leech, John. On the representation of by differences. J. London Math. Soc. 31 (1956), 160--169
- Redei, L.; Ren′i, A. On the representation of the numbers by means of differences. (Russian) Mat. Sbornik N.S. 24(66), (1949). 385--389.
- Golay, Marcel J. E. Notes on the representation of by differences. J. London Math. Soc. (2) 4 (1972), 729--734.
- Pegg, E. Hitting All the Marks: Exploring New Bounds for Sparse Rulers and a Wolfram Language Proof. https://blog.wolfram.com/2020/02/12/hitting-all-the-marks-exploring-new-bounds-for-sparse-rulers-and-a-wolfram-language-proof/
- Sloane, N. J. A. (ed.). "Sequence A326499". The On-Line Encyclopedia of Integer Sequences. OEIS Foundation.