Spectral test

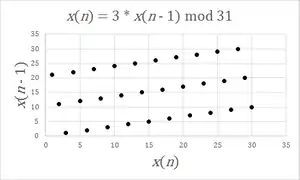
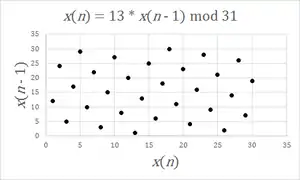
The spectral test is a statistical test for the quality of a class of pseudorandom number generators (PRNGs), the linear congruential generators (LCGs).[1] LCGs have a property that when plotted in 2 or more dimensions, lines or hyperplanes will form, on which all possible outputs can be found.[2] The spectral test compares the distance between these planes; the further apart they are, the worse the generator is.[3] As this test is devised to study the lattice structures of LCGs, it can not be applied to other families of PRNGs.

Three-dimensional plot of 100,000 values generated with RANDU. Each point represents 3 consecutive pseudorandom values. It is clearly seen that the points fall in 15 two-dimensional planes.

According to Donald Knuth,[4] this is by far the most powerful test known, because it can fail LCGs which pass most statistical tests. The IBM subroutine RANDU[5][6] LCG fails in this test for 3 dimensions and above.


Despite the fact that both relations pass the Chi-squared test, the first LCG is less random than the second, as the range of values it can produce by the order it produces them in is less evenly distributed.

References
  1. Williams, K. B.; Dwyer, Jerry (1 Aug 1996), "Testing Random Number Generators, Part 2", Dr. Dobb's Journal, retrieved 26 Jan 2012.
  2. Marsaglia, George (September 1968). "Random Numbers Fall Mainly in the Planes" (PDF). PNAS. 61 (1): 25–28. Bibcode:1968PNAS...61...25M. doi:10.1073/pnas.61.1.25. PMC 285899. PMID 16591687.
  3. Jain, Raj. "Testing Random-Number Generators (Lecture)" (PDF). Washington University in St. Louis. Retrieved 2 December 2016.
  4. Knuth, Donald E. (1981), The Art of Computer Programming volume 2: Seminumerical algorithms (2nd ed.), Addison-Wesley, p. 89.
  5. IBM, System/360 Scientific Subroutine Package, Version II, Programmer's Manual, H20-0205-1, 1967, p. 54.
  6. International Business Machines Corporation (1968). "IBM/360 Scientific Subroutine Package (360A-CM-03X) Version III" (PDF). Stan's Library. White Plains, NY: IBM Technical Publications Department. II: 77. doi:10.3247/SL2Soft08.001. Scientific Application Program H20-0205-3. {{cite journal}}: |author1= has generic name (help)


This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.