Split horizon route advertisement
In computer networking, split-horizon route advertisement is a method of preventing routing loops in distance-vector routing protocols by prohibiting a router from advertising a route back onto the interface from which it was learned.
The concept was suggested in 1974 by Torsten Cegrell, and originally implemented in the ARPANET-inspired Swedish network TIDAS.[1][2][3]
Terminology
Here is some basic terminology:
- Route poisoning: if a node N learns that its route to a destination D is unreachable, inform that to all nodes in the network by sending them a message stating that the distance from N to D, as perceived by N, is infinite.
- Split horizon rule: if a node N uses interface I to transmit to a given destination D, N should not send through I new information about D.
- Poison reverse rule: if a node N uses interface I to transmit to a given destination D, N sends through I the information that its cost-to-go to D is infinite.
Whereas under split horizon N does not send any information through I, under poison reverse node N tells a white-lie.
Example
In this example, network node A routes packets to node B in order to reach node C. The links between the nodes are distinct point-to-point links.

According to the split-horizon rule, node A does not advertise its route for C (namely A to B to C) back to B. On the surface, this seems redundant since B will never route via node A because the route costs more than the direct route from B to C. However, if the link between B and C goes down, and B had received a route from A to C, B could end up using that route via A. A would send the packet right back to B, creating a loop. This is the Count to Infinity Problem. With the split-horizon rule in place, this particular loop scenario cannot happen, improving convergence time in complex, highly-redundant environments.
Split-horizon routing with poison reverse[4] is a variant of split-horizon route advertising in which a router actively advertises routes as unreachable over the interface over which they were learned by setting the route metric to infinite (16 for RIP). The effect of such an announcement is to immediately remove most looping routes before they can propagate through the network.
The main disadvantage of poison reverse is that it can significantly increase the size of routing announcements in certain fairly common network topologies, but it allows for the improvement of the overall efficiency of the network in case of faults. Split horizon states that if a neighboring router sends a route to a router, the receiving router will not propagate this route back to the advertising router on the same interface.
With route poisoning, when a router detects that one of its connected routes has failed, the router will poison the route by assigning an infinite metric to it and advertising it to neighbors. When a router advertises a poisoned route to its neighbors, its neighbors break the rule of split horizon and send back to the originator the same poisoned route, called a poison reverse. In order to give the router enough time to propagate the poisoned route and to ensure that no routing loops occur while propagation occurs, the routers implement a hold-down mechanism.
Poison Reverse
Poison Reverse is often used within distance-vector routing to solve the count-to-infinity problem. Practically, poison reverse can be thought of as an alternative to split horizon. With poison reverse, route advertisements that would be suppressed by split horizon are instead advertised with a distance of infinity.
The basic idea of poison reverse is to make sure that a path does not turn back into the same node if a cost has changed within the network. An example of this would be: Node Z routes via node Y to destination X. If the cost between Y and X increases, the count to infinity problem will occur. To avoid it, we implement poison reverse. As long as Z routes via node Y to get to X, Z will tell a white lie to Y: Z will announce to Y an infinite cost to the destination X.

The numbers on the edges are the costs of the links.
Following this topology, we build the distance vectors of all nodes in the network:
| Destination | to Z | to Y | to X |
| from Z | 0 | 1 | 3 |
| from Y | 1 | 0 | 2 |
| from X | 3 | 2 | 0 |
The first, second and third lines correspond to node Z, node Y and node X distance vectors, respectively.
The following matrix contains the estimates of the distances from Z to all the other nodes in the network through each of its neighbors.
| Destination | via Z | via Y | via X |
| to Z | 0 | X | X |
| to Y | X | 1 | 32 |
| to X | X | 3 | 30 |
As Z routes via Y to get to X, the cost-to-go from Z to X is 3. The poison reverse kicks in when a node broadcasts its distance vector to its neighbors. The distance vectors broadcast by Z are:
To Y: node Z advertises its distance vector, replacing the last element by ∞, i.e., it sends [0, 1, ∞]
To X: node Z advertises its distance vector, without any replacements, i.e., it sends [0, 1, 3]
As we see in the distance vector that is broadcast to node Y the end destination X has an infinity value.
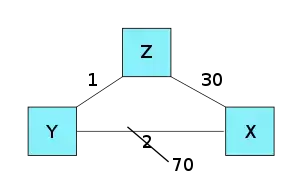
Poison reverse solves the count-to-infinity problem since if the link between Y and X has its cost increased to, say, 70, then Y and Z will not bounce between each other and instead directly try another path. Alternatively, if poison reverse is not used, when the link between Y and X has its cost increased, Y will announce the news to Z. However, before announcing, Y may leverage the fact that Z can reach X with a cost of 3 to decide that Y can reach X with a cost of 4. Then, Z updates its cost-to-go to X, through Y, as 5. Following that, Y updates its cost-to-go to X, through Z, as 6, and so on, until cost-to-go from Z to X reaches 30. At this point, after 30 iterations, the algorithm converges.
Poison reverse doesn't always work. For example:
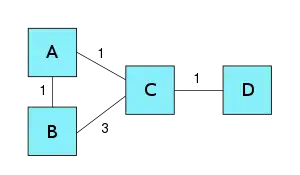
If the link between C and D would fail node C can still try to go through B to get to the destination. B was already routing through A, and will continue doing so. Now, A cannot route through B, due to poison reverse, but at this point A will eventually receive a message from C announcing that C has a route with cost 7 to D, where c(C,B)+distance(B,D)=3+(3+1)=7. Then, A will rely on C to route to D. In summary, after failure of CD, C will update, followed by A, B, C, A, B, C and so on. From there we have a loop that we can not solve with poison reverse.[5]
This can though be completed with an implementation of a distance vector protocol called RIP.
Implementations
The split-horizon method is effective and simple to implement, and is therefore used by most distance-vector protocols. It is notably used by:
See also
- Split-horizon DNS, a similar concept in DNS performing selective publishing of information
- Route poisoning
References
- A Routing Procedure for the TIDAS Message-Switching Network, IEEE Transactions on communication 1975
- Letter from Torsten Cegrell to professor Leonard Kleinroch, 1974-08-19
- Torsten Cegrell - the swede who "fixed" the Internet, Internetmuseum.se, access date 2017-11-09
- IP routing protocols By Uyless D. Black
- https://people.mpi-sws.org/~gummadi/teaching/sp07/datanets/homework/homework2solution.pdf
James F. Kurose; Keith W. Ross (2017). Computer Networking: A top-Down Approach, Seventh Edition. Harlow, England: Pearson. p. 418.
External links
- "Split Horizon" and "Split Horizon with Poison Reverse" in Convergence in RIP Internetworks, from Microsoft TechNet.