Sporadic group
In mathematics, a sporadic group is one of the 26 exceptional groups found in the classification of finite simple groups.
| Algebraic structure → Group theory Group theory |
|---|
 |
A simple group is a group G that does not have any normal subgroups except for the trivial group and G itself. The classification theorem states that the list of finite simple groups consists of 18 countably infinite families[lower-alpha 1] plus 26 exceptions that do not follow such a systematic pattern. These 26 exceptions are the sporadic groups. They are also known as the sporadic simple groups, or the sporadic finite groups. Because it is not strictly a group of Lie type, the Tits group is sometimes regarded as a sporadic group,[1] in which case there would be 27 sporadic groups.
The monster group, or friendly giant, is the largest of the sporadic groups, and all but six of the other sporadic groups are subquotients of it.[2]
Names
Five of the sporadic groups were discovered by Mathieu in the 1860s and the other 21 were found between 1965 and 1975. Several of these groups were predicted to exist before they were constructed. Most of the groups are named after the mathematician(s) who first predicted their existence. The full list is:[1][3][4]
- Mathieu groups M11 (M11), M12 (M12), M22 (M22), M23 (M23), M24 (M24)
- Janko groups J1 (J1), J2 or HJ (J2), J3 or HJM (J3), J4 (J4)
- Conway groups Co1 (Co1), Co2 (Co2), Co3 (Co3)
- Fischer groups Fi22 (Fi22), Fi23 (Fi23), Fi24′ or F3+ (Fi24)
- Higman–Sims group HS
- McLaughlin group McL
- Held group He or F7+ or F7
- Rudvalis group Ru
- Suzuki group Suz or F3−
- O'Nan group O'N (ON)
- Harada–Norton group HN or F5+ or F5
- Lyons group Ly
- Thompson group Th or F3|3 or F3
- Baby Monster group B or F2+ or F2
- Fischer–Griess Monster group M or F1
Various constructions for these groups were first compiled in Conway et al. (1985), including character tables, individual conjugacy classes and lists of maximal subgroup, as well as Schur multipliers and orders of their outer automorphisms. These are also listed online at Wilson et al. (1999), updated with their group presentations and semi-presentations. The degrees of minimal faithful representation or Brauer characters over fields of characteristic p ≥ 0 for all sporadic groups have also been calculated, and for some of their covering groups. These are detailed in Jansen (2005).
An exception found in the classification of sporadic groups within finite simple groups is the Tits group T, that is sometimes also considered as being sporadic — it is almost but not strictly a group of Lie type — which is why in some sources the number of sporadic groups is given as 27, instead of 26.[1] In some other sources, the Tits group is regarded as neither sporadic nor of Lie type.[lower-alpha 2] The Tits group is the (n = 0)-member 2F4(2)′ of the infinite family of commutator groups 2F4(22n+1)′; thus by definition not sporadic. For n > 0 these finite simple groups coincide with the groups of Lie type 2F4(22n+1), also known as Ree groups of type 2F4.
The earliest use of the term sporadic group may be Burnside (1911, p. 504) where he comments about the Mathieu groups: "These apparently sporadic simple groups would probably repay a closer examination than they have yet received."
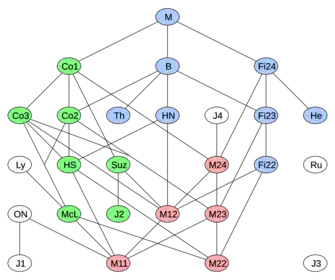
The diagram at right is based on Ronan (2006, p. 247). It does not show the numerous non-sporadic simple subquotients of the sporadic groups.
Organization
Happy Family
Of the 26 sporadic groups, 20 can be seen inside the monster group as subgroups or quotients of subgroups (sections). These twenty have been called the happy family by Robert Griess, and can be organized into three generations.[5][lower-alpha 3]
First generation (5 groups): the Mathieu groups
Mn for n = 11, 12, 22, 23 and 24 are multiply transitive permutation groups on n points. They are all subgroups of M24, which is a permutation group on 24 points.[6]
Second generation (7 groups): the Leech lattice
All the subquotients of the automorphism group of a lattice in 24 dimensions called the Leech lattice:[7]
- Co1 is the quotient of the automorphism group by its center {±1}
- Co2 is the stabilizer of a type 2 (i.e., length 2) vector
- Co3 is the stabilizer of a type 3 (i.e., length √6) vector
- Suz is the group of automorphisms preserving a complex structure (modulo its center)
- McL is the stabilizer of a type 2-2-3 triangle
- HS is the stabilizer of a type 2-3-3 triangle
- J2 is the group of automorphisms preserving a quaternionic structure (modulo its center).
Third generation (8 groups): other subgroups of the Monster
Consists of subgroups which are closely related to the Monster group M:[8]
- B or F2 has a double cover which is the centralizer of an element of order 2 in M
- Fi24′ has a triple cover which is the centralizer of an element of order 3 in M (in conjugacy class "3A")
- Fi23 is a subgroup of Fi24′
- Fi22 has a double cover which is a subgroup of Fi23
- The product of Th = F3 and a group of order 3 is the centralizer of an element of order 3 in M (in conjugacy class "3C")
- The product of HN = F5 and a group of order 5 is the centralizer of an element of order 5 in M
- The product of He = F7 and a group of order 7 is the centralizer of an element of order 7 in M.
- Finally, the Monster group itself is considered to be in this generation.
(This series continues further: the product of M12 and a group of order 11 is the centralizer of an element of order 11 in M.)
The Tits group, if regarded as a sporadic group, would belong in this generation: there is a subgroup S4 ×2F4(2)′ normalising a 2C2 subgroup of B, giving rise to a subgroup 2·S4 ×2F4(2)′ normalising a certain Q8 subgroup of the Monster. 2F4(2)′ is also a subquotient of the Fischer group Fi22, and thus also of Fi23 and Fi24′, and of the Baby Monster B. 2F4(2)′ is also a subquotient of the (pariah) Rudvalis group Ru, and has no involvements in sporadic simple groups except the ones already mentioned.
Table of the sporadic group orders (w/ Tits group)
| Group | Discoverer | [11] Year |
Generation | [4][12] Order |
[1][4] Factorized order |
[13] Minimal faithful Brauer character degree |
[14][15] Generators |
[15][lower-alpha 4] Semi-presentation | |
|---|---|---|---|---|---|---|---|---|---|
| M or F1 | Fischer, Griess | 1973 | 3rd | 80801742479451 | ≈ 8×1053 | 246 · 320 · 59 · 76 · 112 · 133 · 17 · 19 · 23 · 29 · 31 · 41 · 47 · 59 · 71 | 196883 | 2A, 3B, 29 | |
| B or F2 | Fischer | 1973 | 3rd | 41547814812264 | ≈ 4×1033 | 241 · 313 · 56 · 72 · 11 · 13 · 17 · 19 · 23 · 31 · 47 | 4371 | 2C, 3A, 55 | |
| Fi24 or F3+ | Fischer | 1971 | 3rd | 12552 | ≈ 1×1024 | 221 · 316 · 52 · 73 · 11 · 13 · 17 · 23 · 29 | 8671 | 2A, 3E, 29 | |
| Fi23 | Fischer | 1971 | 3rd | 4089470473293004800 | ≈ 4×1018 | 218 · 313 · 52 · 7 · 11 · 13 · 17 · 23 | 782 | 2B, 3D, 28 | |
| Fi22 | Fischer | 1971 | 3rd | 64561751654400 | ≈ 6×1013 | 217 · 39 · 52 · 7 · 11 · 13 | 78 | 2A, 13, 11 | |
| Th or F3 | Thompson | 1976 | 3rd | 90745943887872000 | ≈ 9×1016 | 215 · 310 · 53 · 72 · 13 · 19 · 31 | 248 | 2, 3A, 19 | |
| Ly | Lyons | 1972 | Pariah | 51765179004000000 | ≈ 5×1016 | 28 · 37 · 56 · 7 · 11 · 31 · 37 · 67 | 2480 | 2, 5A, 14 | |
| HN or F5 | Harada, Norton | 1976 | 3rd | 273030912000000 | ≈ 3×1014 | 214 · 36 · 56 · 7 · 11 · 19 | 133 | 2A, 3B, 22 | |
| Co1 | Conway | 1969 | 2nd | 4157776806543360000 | ≈ 4×1018 | 221 · 39 · 54 · 72 · 11 · 13 · 23 | 276 | 2B, 3C, 40 | |
| Co2 | Conway | 1969 | 2nd | 42305421312000 | ≈ 4×1013 | 218 · 36 · 53 · 7 · 11 · 23 | 23 | 2A, 5A, 28 | |
| Co3 | Conway | 1969 | 2nd | 495766656000 | ≈ 5×1011 | 210 · 37 · 53 · 7 · 11 · 23 | 23 | 2A, 7C, 17 | [lower-alpha 5] |
| ON or O'N | O'Nan | 1976 | Pariah | 460815505920 | ≈ 5×1011 | 29 · 34 · 5 · 73 · 11 · 19 · 31 | 10944 | 2A, 4A, 11 | |
| Suz | Suzuki | 1969 | 2nd | 448345497600 | ≈ 4×1011 | 213 · 37 · 52 · 7 · 11 · 13 | 143 | 2B, 3B, 13 | |
| Ru | Rudvalis | 1972 | Pariah | 145926144000 | ≈ 1×1011 | 214 · 33 · 53 · 7 · 13 · 29 | 378 | 2B, 4A, 13 | |
| He or F7 | Held | 1969 | 3rd | 4030387200 | ≈ 4×109 | 210 · 33 · 52 · 73 · 17 | 51 | 2A, 7C, 17 | |
| McL | McLaughlin | 1969 | 2nd | 898128000 | ≈ 9×108 | 27 · 36 · 53 · 7 · 11 | 22 | 2A, 5A, 11 | |
| HS | Higman, Sims | 1967 | 2nd | 44352000 | ≈ 4×107 | 29 · 32 · 53 · 7 · 11 | 22 | 2A, 5A, 11 | |
| J4 | Janko | 1976 | Pariah | 86775571046077562880 | ≈ 9×1019 | 221 · 33 · 5 · 7 · 113 · 23 · 29 · 31 · 37 · 43 | 1333 | 2A, 4A, 37 | |
| J3 or HJM | Janko | 1968 | Pariah | 50232960 | ≈ 5×107 | 27 · 35 · 5 · 17 · 19 | 85 | 2A, 3A, 19 | |
| J2 or HJ | Janko | 1968 | 2nd | 604800 | ≈ 6×105 | 27 · 33 · 52 · 7 | 14 | 2B, 3B, 7 | |
| J1 | Janko | 1965 | Pariah | 175560 | ≈ 2×105 | 23 · 3 · 5 · 7 · 11 · 19 | 56 | 2, 3, 7 | |
| T (or 2F4(2)′) | Tits | 1964 | 3rd | 17971200 | ≈ 2×107 | 211 · 33 · 52 · 13 | 104[16] | 2A, 3, 13 | |
| M24 | Mathieu | 1861 | 1st | 244823040 | ≈ 2×108 | 210 · 33 · 5 · 7 · 11 · 23 | 23 | 2B, 3A, 23 | |
| M23 | Mathieu | 1861 | 1st | 10200960 | ≈ 1×107 | 27 · 32 · 5 · 7 · 11 · 23 | 22 | 2, 4, 23 | |
| M22 | Mathieu | 1861 | 1st | 443520 | ≈ 4×105 | 27 · 32 · 5 · 7 · 11 | 21 | 2A, 4A, 11 | |
| M12 | Mathieu | 1861 | 1st | 95040 | ≈ 1×105 | 26 · 33 · 5 · 11 | 11 | 2B, 3B, 11 | |
| M11 | Mathieu | 1861 | 1st | 7920 | ≈ 8×103 | 24 · 32 · 5 · 11 | 10 | 2, 4, 11 | |
Notes
- The groups of prime order, the alternating groups of degree at least 5, the infinite family of commutator groups 2F4(22n+1)′ of groups of Lie type (containing the Tits group), and 15 families of groups of Lie type.
- For example, in Eric W. Weisstein, "Tits Group", MathWorld there is a link from the Tits group to "Sporadic Group", as opposed to in Eric W. Weisstein, "Sporadic Group", MathWorld, where the Tits group is not listed among the 26 sporadic groups. Both sources checked on 2018-05-26.
- Conway et al. (1985, p. viii) organizes the 26 sporadic groups in likeness:
- "The sporadic simple groups may be roughly sorted as the Mathieu groups, the Leech lattice groups, Fischer's 3-transposition groups, the further Monster centralizers, and the half-dozen oddments."
- Here listed are semi-presentations from standard generators of each sporadic group. Most sporadic groups have multiple presentations & semi-presentations; the more prominent examples are listed.
- Where and with .
References
- Conway et al. (1985, p. viii)
- Griess, Jr. (1998, p. 146)
- Gorenstein, Lyons & Solomon (1998, pp. 262–302)
- Ronan (2006, pp. 244–246)
- Griess, Jr. (1982, p. 91)
- Griess, Jr. (1998, pp. 54–79)
- Griess, Jr. (1998, pp. 104–145)
- Griess, Jr. (1998, pp. 146−150)
- Griess, Jr. (1982, pp. 91−96)
- Griess, Jr. (1998, pp. 146, 150−152)
- Hiss (2003, p. 172)
- Tabelle 2. Die Entdeckung der sporadischen Gruppen (Table 2. The discovery of the sporadic groups)
- Sloane (2015)
- Jansen (2005, pp. 122–123)
- Nickerson & Wilson (2011, p. 365)
- Wilson et al. (1999)
- Lubeck (2001, p. 2151)
Works cited
- Burnside, William (1911). Theory of groups of finite order (2nd ed.). Cambridge: Cambridge University Press. pp. xxiv, 1–512. doi:10.1112/PLMS/S2-7.1.1. hdl:2027/uc1.b4062919. ISBN 0-486-49575-2. MR 0069818. OCLC 54407807. S2CID 117347785.
- Conway, J. H. (1968). "A perfect group of order 8,315,553,613,086,720,000 and the sporadic simple groups". Proc. Natl. Acad. Sci. U.S.A. 61 (2): 398–400. Bibcode:1968PNAS...61..398C. doi:10.1073/pnas.61.2.398. MR 0237634. PMC 225171. PMID 16591697. S2CID 29358882. Zbl 0186.32401.
- Conway, J. H.; Curtis, R. T.; Norton, S. P.; Parker, R. A.; Wilson, R. A. (1985). ATLAS of Finite Groups: Maximal Subgroups and Ordinary Characters for Simple Groups. Oxford: Clarendon Press. pp. xxxiii, 1–252. ISBN 978-0-19-853199-9. MR 0827219. OCLC 12106933. S2CID 117473588. Zbl 0568.20001.
- Gorenstein, D.; Lyons, Richard; Solomon, Ronald (1998). The classification of the finite simple groups, Number 3. Mathematical Surveys and Monographs. Vol. 40. Providence, R.I.: American Mathematical Society. pp. xiii, 1–362. doi:10.1112/S0024609398255457. ISBN 978-0-8218-0391-2. MR 1490581. OCLC 6907721813. S2CID 209854856.
- Griess, Jr., Robert L. (1982). "The Friendly Giant". Inventiones Mathematicae. 69: 1−102. Bibcode:1982InMat..69....1G. doi:10.1007/BF01389186. hdl:2027.42/46608. MR 0671653. S2CID 123597150. Zbl 0498.20013.
- Griess, Jr., Robert L. (1998). Twelve Sporadic Groups. Springer Monographs in Mathematics. Berlin: Springer-Verlag. pp. 1−169. ISBN 9783540627784. MR 1707296. OCLC 38910263. Zbl 0908.20007.
- Hiss, Gerhard (2003). "Die Sporadischen Gruppen (The Sporadic Groups)" (PDF). Jahresber. Deutsch. Math.-Verein. (Annual Report of the German Mathematicians Association). 105 (4): 169−193. ISSN 0012-0456. MR 2033760. Zbl 1042.20007. (German)
- Jansen, Christoph (2005). "The Minimal Degrees of Faithful Representations of the Sporadic Simple Groups and their Covering Groups". LMS Journal of Computation and Mathematics. London Mathematical Society. 8: 122−144. doi:10.1112/S1461157000000930. MR 2153793. S2CID 121362819. Zbl 1089.20006.
- Lubeck, Frank (2001). "Smallest degrees of representations of exceptional groups of Lie type". Communications in Algebra. Philadelphia, PA: Taylor & Francis. 29 (5): 2147−2169. doi:10.1081/AGB-100002175. MR 1837968. S2CID 122060727. Zbl 1004.20003.
- Nickerson, S.J.; Wilson, R.A. (2011). "Semi-Presentations for the Sporadic Simple Groups". Experimental Mathematics. Oxfordshire: Taylor & Francis. 14 (3): 359−371. doi:10.1080/10586458.2005.10128927. MR 2172713. S2CID 13100616. Zbl 1087.20025.
- Ronan, Mark (2006). Symmetry and the Monster: One of the Greatest Quests of Mathematics. New York: Oxford University Press. pp. vii, 1–255. doi:10.1007/s00283-008-9007-9. ISBN 978-0-19-280722-9. MR 2215662. OCLC 180766312. Zbl 1113.00002.
- Sloane, N.J.A., ed. (2015). "Orders of sporadic simple groups (A001228)". The On-Line Encyclopedia of Integer Sequences. OEIS Foundation.
- Wilson, R.A (1998). "Chapter: An Atlas of Sporadic Group Representations" (PDF). The Atlas of Finite Groups - Ten Years On (LMS Lecture Note Series 249). Cambridge, U.K: Cambridge University Press. pp. 261–273. doi:10.1017/CBO9780511565830.024. ISBN 9780511565830. OCLC 726827806. S2CID 59394831. Zbl 0914.20016.
- Wilson, R.A.; Parker, R.A.; Nickerson, S.J.; Bray, J.N. (1999). "ATLAS: Sporadic Groups". ATLAS of Finite Group Representations.