Stacked polytope
In polyhedral combinatorics (a branch of mathematics), a stacked polytope is a polytope formed from a simplex by repeatedly gluing another simplex onto one of its facets.[1][2]
Examples
Every simplex is itself a stacked polytope.
In three dimensions, every stacked polytope is a polyhedron with triangular faces, and several of the deltahedra (polyhedra with equilateral triangle faces) are stacked polytopes


In a stacked polytope, each newly added simplex is only allowed to touch one of the facets of the previous ones. Thus, for instance, the quadaugmented tetrahedron, a shape formed by gluing together five regular tetrahedra around a common line segment is a stacked polytope (it has a small gap between the first and last tetrahedron). However, the similar-looking pentagonal bipyramid is not a stacked polytope, because if it is formed by gluing tetrahedra together, the last tetrahedron will be glued to two triangular faces of previous tetrahedra instead of only one.
Other non-convex stacked deltahedra include:
 |
 |
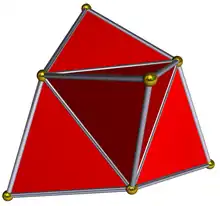 |
| Three tetrahedra | Four tetrahedra | Five tetrahedra |
|---|
Combinatorial structure
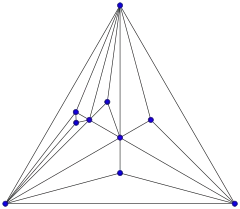
The undirected graph formed by the vertices and edges of a stacked polytope in d dimensions is a (d + 1)-tree. More precisely, the graphs of stacked polytopes are exactly the (d + 1)-trees in which every d-vertex clique (complete subgraph) is contained in at most two (d + 1)-vertex cliques.[3] For instance, the graphs of three-dimensional stacked polyhedra are exactly the Apollonian networks, the graphs formed from a triangle by repeatedly subdividing a triangular face of the graph into three smaller triangles.
One reason for the significance of stacked polytopes is that, among all d-dimensional simplicial polytopes with a given number of vertices, the stacked polytopes have the fewest possible higher-dimensional faces. For three-dimensional simplicial polyhedra the numbers of edges and two-dimensional faces are determined from the number of vertices by Euler's formula, regardless of whether the polyhedron is stacked, but this is not true in higher dimensions. Analogously, the simplicial polytopes that maximize the number of higher-dimensional faces for their number of vertices are the cyclic polytopes.[2]
References
- Grünbaum, Branko (2001), "A convex polyhedron which is not equifacettable" (PDF), Geombinatorics, 10 (4): 165–171, MR 1825338
- Miller, Ezra; Reiner, Victor; Sturmfels, Bernd, Geometric Combinatorics, IAS/Park City mathematics series, vol. 13, American Mathematical Society, p. 621, ISBN 9780821886953.
- Koch, Etan; Perles, Micha A. (1976), "Covering efficiency of trees and k-trees", Proceedings of the Seventh Southeastern Conference on Combinatorics, Graph Theory, and Computing (Louisiana State Univ., Baton Rouge, La., 1976), Congressus Numerantium, Winnipeg, Manitoba, Canada: Utilitas Mathematica, 17: 391–420, MR 0457265. See in particular p. 420.