Stromquist moving-knives procedure

Stromquist moving-knife procedure when cake is cut

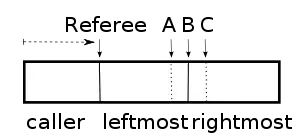
A referee moves a sword from left to right over the cake, hypothetically dividing it into small left piece and a large right piece. Each player moves a knife over the right piece, always keeping it parallel to the sword. The players must move their knives in a continuous manner, without making any "jumps".[3] When any player shouts "cut", the cake is cut by the sword and by whichever of the players' knives happens to be the central one of the three (that is, the second in order from the sword). Then the cake is divided in the following way:

• The piece to the left of the sword, which we denote Left, is given to the player who first shouted "cut". We call this player the "shouter" and the other two players the "quieters".
• The piece between the sword and the central knife, which we denote Middle, is given to the remaining player whose knife is closest to the sword.
• The remaining piece, Right, is given to the third player.

Each player can act in a way that guarantees that—according to their own measure—no other player receives more than them:

• Always hold your knife such that it divides the part to the right of the sword to two pieces that are equal in your eyes (hence, your knife initially divides the entire cake to two equal parts and then moves rightwards as the sword moves rightwards).
• Shout 'cut' when Left becomes equal to the piece you are about to receive if you remain quiet (i.e. if your knife is leftmost, shout 'cut' if Left=Middle; if your knife is rightmost, shout if Left=Right; if your knife is central, shout 'cut' if Left=Middle=Right).

We now prove that any player using the above strategy receives an envy-free share.

First, consider the two quieters. Each of them receives a piece that contains their own knife, so they do not envy each other. Additionally, because they remained quiet, the piece they receive is larger in their eyes than Left, so they also don't envy the shouter.

The shouter receives Left, which is equal to the piece they could receive by remaining silent and larger than the third piece, hence the shouter does not envy any of the quieters.

Following this strategy each person gets the largest or one of the largest pieces by their own valuation and therefore the division is envy-free.

The same analysis shows that the division is envy-free even in the somewhat degenerate case when there are two shouters, and the leftmost piece is given to any of them.

The moving-knives procedure can be adapted for chore division - dividing a cake with a negative value.[4]^{: exercise 5.11}

• The Fair pie-cutting procedure provides a simpler solution to the same problem, using only 3 rotating knives, when the cake is a 1-dimensional circle ("pie"),
• The Robertson–Webb rotating-knife procedure provides an even simpler solution, using only 1 rotating knife, when the cake is 2-dimensional.
• Moving-knife procedure