Surface properties of transition metal oxides
Transition metal oxides are compounds composed of oxygen atoms bound to transition metals. They are commonly utilized for their catalytic activity and semiconducting properties. Transition metal oxides are also frequently used as pigments in paints and plastics, most notably titanium dioxide. Transition metal oxides have a wide variety of surface structures which affect the surface energy of these compounds and influence their chemical properties. The relative acidity and basicity of the atoms present on the surface of metal oxides are also affected by the coordination of the metal cation and oxygen anion, which alter the catalytic properties of these compounds. For this reason, structural defects in transition metal oxides greatly influence their catalytic properties. The acidic and basic sites on the surface of metal oxides are commonly characterized via infrared spectroscopy, calorimetry among other techniques. Transition metal oxides can also undergo photo-assisted adsorption and desorption that alter their electrical conductivity. One of the more researched properties of these compounds is their response to electromagnetic radiation, which makes them useful catalysts for redox reactions, isotope exchange and specialized surfaces.
Surface structure and stability
There is very little known about the surface structures of transition metal oxides, but their bulk crystal structures are well researched. The approach to determine the surface structure is to assume the oxides are ideal crystal, where the bulk atomic arrangement is maintained up to and including the surface plane. The surfaces will be generated by cleavages along the planes of the bulk crystal structure.[1] However, when a crystal is cleaved along a particular plane, the position of surface ions will differ from the bulk structure. Newly created surfaces will tend to minimize the surface Gibbs energy, through reconstruction, to obtain the most thermodynamically stable surface.[2] The stability of these surface structures are evaluated by surface polarity, the degree of coordinative unsaturation and defect sites.
Bulk structures
The oxide crystal structure is based on a close-pack array of oxygen anions, with metal cations occupying interstitial sites.[1] The close-packed arrays, such as face-centered-cubic (fcc) and hexagonal-close packed (hcp), have both octahedral and tetrahedral interstices.[3]
Monoxides
Many compounds from first row of transition metal monoxides (MO), from TiO to NiO, have a rocksalt structure. The rock salt structure[4] is generated by filling all octahedral sites with cations in an oxygen anion fcc array.[5][6]
Dioxides

The majority of transition metal dioxides (MO2) have the rutile structure, seen to the right. Materials of this stoichiometry exist for Ti, Cr, V and Mn in the first row transition metal and for Zr to Pd in the second. The rutile structure is generated by filling half of the octahedral sites with cations of the hcp oxygen anion array.[5][6]
Trioxides
Few transition metals can achieve the +6 oxidation state in an oxide, so oxides with the stoichiometry MO3 are rare.[7]
Ternary oxides
The structure of binary oxides can be predicted on the basis of the relative sizes of the metal and oxide ions and the filling of holes in a close packed oxide lattice. However, the predictions of structure are more difficult for ternary oxides. The combination of two or more metals in an oxide creates a lot of structural possibilities. Also, the stoichiometry of ternary oxide may be changed by varying the proportions of the two components and their oxidation states. For example, at least twenty ternary oxide phases are formed between strontium and vanadium including SrV2O6, Sr2V2O5, SrVO3 and Sr2VO4.[7] The structural chemistry of ternary and more complex oxides is an extensive subject, but there are a few structures that are widely adopted by ternary oxides, such as the perovskite structure.
Perovskite structure
The perovskite structure, ABO3, is the most widespread ternary phase. The perovskite structure is frequently found for ternary oxides formed with one large (A) and one small cation (B). In this structure, there is a simple cubic array of B cations, with the A cations occupying the center of the cube, and the oxide atoms are sited at the center of the 12 edges of the simple cube.[8][5][6][7]
Surface stability
Since very little is known about the surface Gibbs energy of transition metal oxides, polarity of the surface and the degree of coordinative unsaturation of a surface cation are used to compare the stabilities of different surface structures.[2] Also, defect sites can have a huge impact on the surface stability.
Polarity of the surface
When a crystal of a binary oxide is cleaved to generate two new surfaces, each solid's charge remains neutral. However, the structure of the two newly created surfaces may or may not be the same. If the structures are identical, the surface will be dipoleless and is considered a nonpolar surface. If the structures are different, the surface will have a strong dipole and is considered a polar surface. Examples of nonpolar surfaces include the rocksalt (100) surface, the rutile (100), (110) and (001) surfaces and the pervoskite (100) surface.[2] An example of a polar surface is the rocksalt (111) surface.[2] In general, a polar surface is less stable than a nonpolar surface because a dipole moment increases the surface Gibbs energy. Also, oxygen polar surfaces are more stable than metal polar surfaces because oxygen ions are more polarizable, which lowers the surface energy.[9]
The degree of coordinative unsaturation of a surface cation
The degree of coordinative unsaturation of a surface cation measures the number of bonds involving the cation that have to be broken to form a surface.[2] As the degree of coordinative unsaturation increases, more bonds are broken and the metal cation becomes destabilized. The destabilization of the cation increases the surface Gibbs energy, which decreases the overall stability. For example, the rutile (110) surface is more stable than the rutile (100) and (001) surfaces because it has a lower degree of coordinative unsaturation.[2]
Defect sites

Defect sites can interfere with the stability of metal oxide surfaces, so it is important to locate and determine methods to control these sites. Oxides exhibit an abundance of point defect sites. In rocksalt surfaces, oxygen and metal cation vacancies are the most common point defects. The vacancies are produced by electron bombardment and annealing to extremely high temperatures. However, oxygen vacancies are more common and have a greater impact than metal cation vacancies. Oxygen vacancies cause reduction in between surface cations, which significantly affect the electronic energy levels.[10] Steps and kinks are two other defects that impact rocksalt surfaces. These structural defects reduce the coordination environment of the four adjacent surface cations from 5 to 4.[11] In rutile surfaces, the most common type of defect is oxygen vacancies. There are two types of oxygen vacancies, which result from either the removal of a bridging O2− ions or the removal of an inplane O2− ion. Both of these will reduce the coordination of the surface cations.[12][10][13]
Surface acidity/basicity
Extension of acid/base theories to solids
The surface of a metal oxide consists of ordered arrays of acid–base centres. The cationic metal centres act as Lewis acid sites while the anionic oxygen centres act as Lewis bases. Surface hydroxyl groups can serve as Brønsted acid or base sites as they can give up or accept a proton.[14] The surface of most metal oxides will be, to some extent, hydroxylated under normal conditions when water vapor is present.[15] The strength and the amount of Lewis And Brønsted acid–base sites will determine the catalytic activity of many metal oxides. Due to this there is a great need to develop standard methods for the characterization of the strength, concentration, and distribution of surface acid–base sites.[14]
The concepts of Lewis acid–base theory and Brønsted–Lowry acid–base theory may be applied to surfaces, however there is no general theory that serves to determine surface acidity or basicity.[16] The qualitative treatment of Brønsted acid base theory is based on the thermodynamic equilibrium constant (Ka) of acid–base reactions between individual molecules in homogeneous systems. This treatment requires measurement of equilibrium concentrations of reactants and products. The presence of two phases also provides a problem for the quantitative acid–base determination of solids. When an acid or base is adsorbed on to an oxide surface it will perturb neighbouring acid–base sites.[17] This perturbation will inevitably influence the relaxation of the surface and make it impossible to have acid–base reactions at the surface which only involve a single surface site.
Structural relation to surface acidity/basicity
For metal oxides acidity and basicity are dependent on the charge and the radius of the metal ions as well as the character of the metal oxygen bond. The bond between oxygen and the metal is influenced by the coordination of the metal cations and the oxygen anions as well as the filling of the metal d-orbitals.[16] The surface coordination is controlled by the face that is exposed and by the surface relaxation. Structural defects can greatly contribute to the acidity or basicity as sites of high unsaturation can occur from oxygen or metal ion vacancies.
Indicator method
Adsorption of an indicator molecule was first proposed by Hammett for ordering the strength of solid acids and bases.[14] This technique is only applicable to surface Brønsted sites on metal oxides. According to Hammett, the strength of a Brønsted surface site can be determined by the Hammett acidity function,
where B is the basic indicator molecule. The concentration of Brønsted acid sites can be determined by titrating a suspension of the oxide with an acid/base indicator present.[14] However, this method is subject to many problems. For instance only Bronsted acid sites can be quantified with this method. Metal oxide surfaces can have both Brønsted and Lewis acid sites present at the same time which leads to a nonspecific interaction between the oxide and the indicator.[16] Also, as outlined in the theory section, the perturbation of neighboring sites upon adsorption of indicator molecules compromises the integrity of this model.[17]
IR determination of adsorbed probe molecules
The adsorption of a very weakly basic or acidic probe molecule can serve to give a picture of Brønsted and Lewis acid–base sites. Infrared spectroscopy of surface sites and adsorbed molecules can then be used to monitor the change in the vibrational frequencies upon adsorption.[14] A very weakly acidic probe molecule can be used to minimize disturbing neighboring sites so that a more accurate measure of surface acidity or basicity can be obtained. A variety of probe molecules can be used including: ammonia, pyridine, acetonitrile, carbon monoxide,[18] and carbon dioxide.[14][16]
Calorimetric and thermal desorption
Two promising methods for the description of the acid–base properties of metal oxides are Calorimetric measurements of adsorption enthalpies and Temperature Programmed desorption.[16] The measurement of the heat of adsorption of basic or acidic probe molecules can give a description of acidic and basic sites on metal oxide surfaces. Temperature programmed desorption provides information about acid–base properties by saturating the surface with a probe molecule and measuring the amount that desorbs from the surface as a function of temperature. The calorimetric method provides a quantitative thermodynamic scale of acetate properties by measuring the heat of adsorption. Calorimetric methods can be considered to give a measure of the total acidity or basicity as it is not discriminate to either Lewis or Brønsted sites. However, when differential heats of adsorption are combined with other techniques, such as IR spectroscopy, the nature and distribution of acid–base adsorption sites can be obtained.[19]
ZrO2
Zirconia exists in the monoclinic, tetragonal or cubic crystal system depending on the temperature. The surface acidity and basicity of the oxide depends on the crystal structure and surface orientation.[20] The surfaces of zirconia have hydroxyl groups, which can act as Brønsted acids or bases, and coordination-unsaturated Zr4+O2− acid base pairs which contribute to its overall acid–base properties.[20] Adsorption studies have shown that monoclinic zirconia is more basic than tetragonal, as it forms stronger bonds with CO2. Adsorption of CO shows that the tetragonal phase has more acidic Lewis acid sites than the monoclinic phase, but that it has a lower concentration of Lewis acid sites.[20]
Photoassisted processes
Electronic band structure
The bulk electronic band structure of transition metal oxides consists of overlapping 2p orbitals from oxygen atoms, forming the lower energy, highly populated valence band, while the sparsely populated, higher energy conduction band consists of overlapping d orbitals of the transition metal cation.[21] In contrast to metals, having a continuous band of electronic states, semiconductors have a band gap that prevents the recombination of electron/hole pairs that have been separated into the conduction band/ valence band. The nanosecond scale life times of these electron/hole separations allows for charge transfer to occur with an adsorbed species on the semiconductor surface. The Potential of an acceptor must be more positive than the conduction band potential of the semiconductor in order for reduction of the species to commence. Conversely, the potential of the donor species must be more negative than that of the valence band of the semiconductor for oxidation of the species to occur.[22]
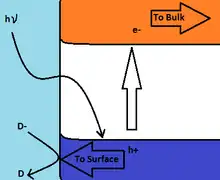
Near the surface of a semi-conducting metal oxide the valence and conduction bands are of higher energy, causing the upward bending of the band energy as shown in the band energy diagram, such that promotion of an electron from the valence band to the conduction band by light of energy greater than the band gap results in migration of the electron towards the bulk of the solid or to a counter electrode, while the hole left in the valence band moves towards the surface. The increased concentration of holes near the surface facilitates electron transfer to the solid, such as the example shown in the figure of the oxidation of redox couple D-/D.[2] In the absence of any mechanism to remove electrons from the bulk of the solid irradiation continues to excite electrons to the conduction band producing holes in the valence band. This leads to the reduction of the upward bending of the band energies near the surface, and the subsequent increase in excited electron availability for reduction reactions.[2]
The following equations are useful in describing the populations of valence and conduction bands in terms of holes and electrons for the bulk metal. is the density of electrons in the bulk metal conduction band, and is the density of holes in the bulk metal valence band. Ec is the lowest energy of the conduction band, Ef is the Fermi energy (electrochemical energy of the electrons), Ev is the highest energy of the valence band, Nc is the effective mass and mobility of an electron in the conduction band (constant), and Nv is the effective mass and mobility of a valence band hole (constant).[2]
where k is Boltzmanns constant and T is the absolute temperature in kelvins.
The use of quantum mechanics perturbation theory can aid in calculating the probability of an electronic transition taking place. The probability is proportional to the square of the amplitude of the radiation field, E0, and the square of the transition dipole moment |μif|.[22]
The quantum yield for an ideal system undergoing photocatalytic events is measured as the number of events occurring per photon absorbed. The typical assumption in determining the quantum yield is that all photons are absorbed on the semiconductor surface, and the quantum yield is referred to as the apparent quantum yield. This assumption is necessary due to the difficulty in measuring the actual photons absorbed by the solid surface. The relation between the quantum yield, the rate of charge transfer, kCT, and the electron/hole recombination rate, kR, is given by the following equation.[22]
Photoinduced molecular transformations at transition metal oxide surfaces can be organized in two general classes. Photoexcitation of the adsorbate which then reacts with the catalyst substrate is classified as a catalyzed photoreaction. Photoexcitation of the catalyst followed by interaction of the catalyst with a ground state reactant is classified as a sensitized photoreaction.[22]
Photo-assisted adsorption and desorption
Adsorption and desorption can both be promoted by exposure of trans metal oxides to light, the predominant process being controlled by experimental conditions. Adsorption of oxygen by illumination of TiO2 or ZnO at room temperature with low pressure results in the adsorption of oxygen, while at high pressures illumination leads to photo-assisted desorption. At high temperatures the opposite effect is observed, with low pressure leading to desorption, and high pressure causing adsorption.[2][23] Kase et al. conducted a study of the photo-assisted chemisorption of NO on ZnO, finding that under dark conditions a negligible amount of NO was adsorbed to the metal oxide, however under illumination ZnO irreversibly adsorbs NO, their sample showing no desorption after irradiation was stopped.[23]
The process by which adsorption and desorption on metal oxide surfaces takes place is related to the photo generation of holes on the solid surface, which are believed to be trapped by hydroxyl groups on the surface of a transition metal oxides.[22][23] These trapped holes allow photo-excited electrons to be available for chemisorption.[23] Doping of a cation of either higher or lower valence can change the electronic properties of the metal oxide. Doping with a higher valence cation typically results in an increase in n-type semi-conductivity, or raises its Fermi energy, while doping with a lower valence cation should lower the Fermi energy level and reduce the metal oxide's n-type semi-conductivity.[24] The process of doping indicates that a cation other than the transition metal cation experienced in the majority of the bulk is incorporated into the crystal structure of the semiconductor, either by replacing the cation, or interstitially adding to the matrix.[24] Doping of ZnO with Li leads to greater photo-adsorption of oxygen, while doping with Ga or Al suppresses photo-adsorption of oxygen. Trends in photo-adsorption tend to follow trends in photo-oxidative catalysis, as shown by the high degree of photo-oxidative catalytic activity of TiO2 and ZnO, while other transition elements like V2O5 shows no photo-oxidative catalytic response as well as no photo-activated adsorption of oxygen.[2]
Liquid-phase photocatalysis
One of the most exciting and most studied uses of photocatalysis is the photo-oxidation of organics as it applies to environmental decontamination.[21] In contrast to gas phase interactions with the solid surface, the vast number of variables associated with the liquid solid interface (i.e. solution pH, photocatalyst concentration, solvent effects, diffusion rate, etc.) calls for greater care to be taken to control these variables to produce consistent experimental results.[21][22] A greater variety of reactions also become possible due to the ability of solutions to stabilize charged species, making it possible to add an electron from the metal to a neutral species producing an anion that can go on to further react, or a hole to remove an electron, producing a cation that goes on to further react in solution.[2]
Oxidation
One mechanism proposed for the oxidation of adsorbed organics from solution is the production of hydroxyl radical by the valence holes migrating to the surface and reacting with adsorbed hydroxyl groups, resulting in a very strong oxidizing radical. Identification of hydroxylated oxidation intermediates and hydroxyl radicals supports this proposed mechanism, however this does not negate the possibility of the direct oxidation of the organic reactant by the valence holes because similar intermediates would be expected in either case.[22] Some photo-oxidation reactions are shown below.
| Starting material | Photo-oxidized product | Metal oxide catalyst |
|---|---|---|
| C2O42− + O2 + 2 H2O | 2 CO2 + 2 OH− + H2O2 | ZnO[2] |
| (CH3)2CHOH + O2 | (CH3)2CO + H2O2 | ZnO[2] |
| CH3CO2− + h+ | C2H6 + CO2 | Rutile TiO2[2] |
| H2O | H2 + 1⁄2O2 | RuO2−TiO2−Pt [22] |
Reduction
In photo reduction the promoted electron of the metal oxide is accepted by an acceptor species. In the case of CO2 reduction, shown in the table below, the absence of dissolved oxygen in the aqueous system favors reduction of protons to form hydrogen radicals which then go on to reduce CO2 to HCOOH. HCOOH can then be further reduced to HCOH and water. Further reduction leads to the production of CH3• that can combine in a number of ways to produce CH4 or C2H6, etc.[25]
| Starting material | Reduction product | Metal oxide |
|---|---|---|
| Cu2+ | Cu0 | TiO2[2] |
| Pt4+ | Pt0 | TiO2[2] |
| Cr(VI) | Cr(III) | TiO2 or SO42−/TiO2 [26] |
| CO2 + H2O | C1-C3 (I.E. C2H5OH, C2H6, etc.) | ZnO or TiO2 on basic support [25] |
Gas-phase photocatalysis
Metal oxides excel at catalyzing gas phase reactions by photo-activation, as well as thermal activation of the catalyst. Oxidation of hydrocarbons, alcohols, carbon monoxide, and ammonia occurs when stimulated with light of greater energy than the band gap of the metal oxide.[22][2] Homophasic and heterophasic light-induced oxygen isotope exchange has also been observed over TiO2 and ZnO. Homophasic isotope exchange is the production of 216O18O(g) from 16O2(g) and 18O2(g). Heterophasic isotope exchange is the chemisorption of an oxygen isotope to the lattice of the metal oxide (lat), and replacement of one of the oxygens in the gas phase with the lattice oxygen as shown in the following reaction.[2]
18O2(g) + 16Olat → 16O18O(g) + 18Olat
References
- Henrich, V.E. (1994). The Surface Science of Metal Oxides. New York: Cambridge University Press. pp. 14–61.
- Kung, Harold (1989). Transition Metal Oxides: Surface Chemistry and Catalysis. Amsterdam: Elsevier Science Publishers B.V. pp. 252–272. ISBN 9780080887425.
- "Chem 101(SEAS) Ionic Crystal Structures". www.seas.upenn.edu. Archived from the original on 1999-11-16.
- "Chem 101(SEAS) Ionic Crystal Structures". www.seas.upenn.edu. Archived from the original on 1999-11-16.
- West, A (2000). Basic Solid State Chemistry. New York: Wiley.
- EveryScience. "Ionic Solids". Retrieved 7 June 2011.
- Weller, Mark. "Transition Metal Oxides" (PDF). University of Southampton. Retrieved 7 June 2011.
- "Perovskite and Related Structures". cst-www.nrl.navy.mil. Archived from the original on 1999-11-03.
- Al-Abadleh, Hind (2003). "Oxide surfaces as environmental interfaces". Surface Science Reports. 52 (3–4): 63–161. Bibcode:2003SurSR..52...63A. doi:10.1016/j.surfrep.2003.09.001.
- Henrich, V (1988). Surface and Near-surface Chemistry of Oxide Materials. Amsterdam: Elsevier. pp. 23–30.
- Liu, P (1998). "Reaction of water with MgO(100) surfaces. Part II". Surface Science. 412–413 (1–2): 315–332. Bibcode:1998SurSc.412..315L. doi:10.1016/S0039-6028(98)00445-2.
- http://www.ndt-ed.org/EducationResources/CommunityCollege/Materials/Structure/point_defects.htm
- Bart, F (1994). "A LEED study of the (0001) α-quartz surface reconstruction". Surface Science. 311 (1): L671–L676. Bibcode:1994SurSc.311L.671B. doi:10.1016/0039-6028(94)90471-5.
- Glazneva, T. S.; Kotsarenko, N. S.; Paukshtis, E. A. (2008). "Surface acidity and basicity of oxide catalysts: From aqueous suspensions to in situ measurements". Kinetics and Catalysis. 49 (6): 856–867. doi:10.1134/S0023158408060104. S2CID 97237926.
- Boehm, H. P. (1971). "Acidic and basic properties of hydroxylated metal oxide surfaces". Discussions of the Faraday Society. 52: 264–275. doi:10.1039/df9715200264.
- Abee, M. W. (2001) Interaction of acid/base probe molecules with specific features on well-defined metal oxide single-crystal surfaces. PhD Thesis, Virginia Tech University.
- Zecchina, Adriano; Lamberti, Carlo; Bordiga, Silvia (1998). "Surface acidity and basicity: General concepts". Catalysis Today. 41 (1–3): 169–177. doi:10.1016/S0920-5861(98)00047-9.
- Deiana, C.; Fois, E.; Martra, G.; Narbey, S.; Pellegrino, F.; Tabacchi, G. (April 2016). "On the Simple Complexity of Carbon Monoxide on Oxide Surfaces: Facet-Specific Donation and Backdonation Effects Revealed on TiO2 Anatase Nanoparticles". ChemPhysChem. 17 (13): 1956–1960. doi:10.1002/cphc.201600284. hdl:11383/2057445. PMID 27003518.
- Auroux, Aline.; Gervasini, Antonella. (1900). "Microcalorimetric study of the acidity and basicity of metal oxide surfaces". J. Phys. Chem. 94 (16): 6371–6379. doi:10.1021/j100379a041.
- Pokrovski, Konstantin; Jung, Kyeong Taek; Bell, Alexis T. (2001). "Investigation of CO and CO2 Adsorption on Tetragonal and Monoclinic Zirconia". Langmuir. 17 (14): 4297–4303. doi:10.1021/la001723z.
- Miyauchi, Masahiro (1999). "Photoinduced Surface Reactions on TiO2 and SrTiO3 Films: Photocatalytic Oxidation and Photoinduced Hydrophilicity". Chem. Mater. 12: 3–5. doi:10.1021/cm990556p.
- Linsebigler, Amy L.; Lu, Guangquan.; Yates, John T. (1995). "Photocatalysis on TiO2 Surfaces: Principles, Mechanisms, and Selected Results" (PDF). Chem. Rev. 95 (3): 735–758. doi:10.1021/cr00035a013. S2CID 53343077.
- Kase, K.; Yamaguchi, M.; Suzuki, T.; Kaneko, K. (1995). "Photoassisted Chemisorption of NO on ZnO". Journal of Physical Chemistry. 99 (36): 13307–13309. doi:10.1021/j100036a002.
- Ioannides, Theophilos; Verykios, Xenophon E. (1993). "Effects of altervalent cation doping of TiO2 on H2 and CO adsorption on supported Rh". Journal of Catalysis. 145 (2): 479–490. doi:10.1006/jcat.1994.1058.
- Subrahmanyam, M. (1999). "A Screening for the Photo Reduction of Carbon Dioxide Supported on Metal Oxide Catalysts for C1-C3 Selectivity" (PDF). Applied Catalysis B: Environmental. 23 (2–3): 169–174. doi:10.1016/S0926-3373(99)00079-X. Retrieved 2 June 2011.
- Jiang, Fang (2006). "Aqueous Cr(VI) Photo-Reduction Catalyzed by TiO2 and Sulfated TiO2". Journal of Hazardous Materials. 134 (1–3): 94–103. doi:10.1016/j.jhazmat.2005.10.041. PMID 16310949.