Surface plasmon

Surface plasmons (SPs) are coherent delocalized electron oscillations that exist at the interface between any two materials where the real part of the dielectric function changes sign across the interface (e.g. a metal-dielectric interface, such as a metal sheet in air). SPs have lower energy than bulk (or volume) plasmons which quantise the longitudinal electron oscillations about positive ion cores within the bulk of an electron gas (or plasma).

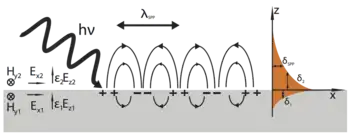
Schematic representation of an electron density wave propagating along a metal–dielectric interface. The charge density oscillations and associated electromagnetic fields are called surface plasmon-polariton waves. The exponential dependence of the electromagnetic field intensity on the distance away from the interface is shown on the right. These waves can be excited very efficiently with light in the visible range of the electromagnetic spectrum.

The charge motion in a surface plasmon always creates electromagnetic fields outside (as well as inside) the metal. The total excitation, including both the charge motion and associated electromagnetic field, is called either a surface plasmon polariton at a planar interface, or a localized surface plasmon for the closed surface of a small particle.

The existence of surface plasmons was first predicted in 1957 by Rufus Ritchie.[1] In the following two decades, surface plasmons were extensively studied by many scientists, the foremost of whom were T. Turbadar in the 1950s and 1960s, and E. N. Economou, Heinz Raether, E. Kretschmann, and A. Otto in the 1960s and 1970s. Information transfer in nanoscale structures, similar to photonics, by means of surface plasmons, is referred to as plasmonics.[2]

Surface plasmon polaritons
Main article: Surface plasmon polariton

Excitation
Main article: Surface plasmon polariton § Excitation

Surface plasmon polaritons can be excited by electrons[3] or photons. In the case of photons, it cannot be done directly, but requires a prism, or a grating, or a defect on the metal surface.[4]

Dispersion relation
Lossless dispersion curve for surface plasmons. At low k, the surface plasmon curve (red) approaches the photon curve (blue)
Main article: Surface plasmon polariton § Fields and dispersion relation

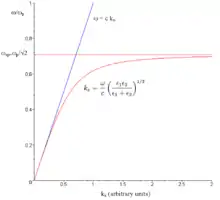
At low frequency, an SPP approaches a Sommerfeld-Zenneck wave, where the dispersion relation (relation between frequency and wavevector) is the same as in free space. At a higher frequency, the dispersion relation bends over and reaches an asymptotic limit called the "plasma frequency"[4] (see figure at right).[lower-alpha 1] For more details see surface plasmon polariton.

Propagation length and skin depth
Main article: Surface plasmon polariton § Propagation length and skin depth

As an SPP propagates along the surface, it loses energy to the metal due to absorption. It can also lose energy due to scattering into free-space or into other directions. The electric field falls off evanescently perpendicular to the metal surface. At low frequencies, the SPP penetration depth into the metal is commonly approximated using the skin depth formula. In the dielectric, the field will fall off far more slowly. SPPs are very sensitive to slight perturbations within the skin depth and because of this, SPPs are often used to probe inhomogeneities of a surface.[4] For more details, see surface plasmon polariton.

Localized surface plasmons
Condensed matter physics
States of matter
Phase phenomena
Electronic phases
Electronic phenomena
Magnetic phases
Quasiparticles
Soft matter
Scientists
Main article: Localized surface plasmon

Localized surface plasmons arise in small metallic objects, including nanoparticles. Since the translational invariance of the system is lost, a description in terms of wavevector, as in SPPs, can not be made. Also unlike the continuous dispersion relation in SPPs, electromagnetic modes of the particle are discretized.[7]

LSPs can be excited directly through incident waves; efficient coupling to the LSP modes correspond to resonances and can be attributed to absorption and scattering, with increased local-field enhancements.[7] LSP resonances largely depend on the shape of the particle; spherical particles can be studied analytically by Mie theory.[4][7]

Experimental applications

The excitation of surface plasmons is frequently used in an experimental technique known as surface plasmon resonance (SPR). In SPR, the maximum excitation of surface plasmons are detected by monitoring the reflected power from a prism coupler as a function of incident angle or wavelength. This technique can be used to observe nanometer changes in thickness, density fluctuations, or molecular absorption. Recent works have also shown that SPR can be used to measure the optical indexes of multi-layered systems, where ellipsometry failed to give a result.[8][9]

Surface plasmon-based circuits have been proposed as a means of overcoming the size limitations of photonic circuits for use in high performance data processing nano devices.[10]

The ability to dynamically control the plasmonic properties of materials in these nano-devices is key to their development. A new approach that uses plasmon-plasmon interactions has been demonstrated recently. Here the bulk plasmon resonance is induced or suppressed to manipulate the propagation of light.[11] This approach has been shown to have a high potential for nanoscale light manipulation and the development of a fully CMOS-compatible electro-optical plasmonic modulator, said to be a future key component in chip-scale photonic circuits.[12]

Some other surface effects such as surface-enhanced Raman scattering and surface-enhanced fluorescence are induced by surface plasmon of noble metals, therefore sensors based on surface plasmons were developed.[13]

In surface second harmonic generation, the second harmonic signal is proportional to the square of the electric field. The electric field is stronger at the interface because of the surface plasmon resulting in a non-linear optical effect. This larger signal is often exploited to produce a stronger second harmonic signal.[14]

The wavelength and intensity of the plasmon-related absorption and emission peaks are affected by molecular adsorption that can be used in molecular sensors. For example, a fully operational prototype device detecting casein in milk has been fabricated. The device is based on monitoring changes in plasmon-related absorption of light by a gold layer.[15]

See also

Notes
  1. This lossless dispersion relation neglects the effects of damping factors, such as the intrinsic losses in metals. For lossy cases, the dispersion curve backbends after the reaching the surface plasmon frequency instead of asymptotically increasing.[5][6]

References
  1. Ritchie, R. H. (June 1957). "Plasma Losses by Fast Electrons in Thin Films". Physical Review. 106 (5): 874–881. Bibcode:1957PhRv..106..874R. doi:10.1103/PhysRev.106.874.
  2. Polman, Albert; Harry A. Atwater (2005). "Plasmonics: optics at the nanoscale" (PDF). Materials Today. 8: 56. doi:10.1016/S1369-7021(04)00685-6. Retrieved January 26, 2011.
  3. Bashevoy, M.V.; Jonsson, F.; Krasavin, A.V.; Zheludev, N.I.; Chen Y.; Stockman M.I. (2006). "Generation of traveling surface plasmon waves by free-electron impact". Nano Letters. 6: 1113. arXiv:physics/0604227. doi:10.1021/nl060941v.
  4. Maradudin, Alexei A.; Sambles, J. Roy; Barnes, William L., eds. (2014). Modern Plasmonics. Amsterdam: Elsevier. p. 1–23. ISBN 9780444595263.
  5. Arakawa, E. T.; Williams, M. W.; Hamm, R. N.; Ritchie, R. H. (29 October 1973). "Effect of Damping on Surface Plasmon Dispersion". Physical Review Letters. 31 (18): 1127–1129. doi:10.1103/PhysRevLett.31.1127.
  6. Maier, Stefan A. (2007). Plasmonics: Fundamentals and Applications. New York: Springer Publishing. ISBN 978-0-387-33150-8.
  7. Le Ru, Eric C.; Etchegoin, Pablo G. (2009). Principles of Surface-Enhanced Raman Spectroscopy. Amsterdam: Elsevier. p. 174–179. ISBN 978-0-444-52779-0.
  8. Taverne, S.; Caron, B.; Gétin, S.; Lartigue, O.; Lopez, C.; Meunier-Della-Gatta, S.; Gorge, V.; Reymermier, M.; Racine, B.; Maindron, T.; Quesnel, E. (2018-01-12). "Multispectral surface plasmon resonance approach for ultra-thin silver layer characterization: Application to top-emitting OLED cathode". Journal of Applied Physics. 123 (2): 023108. Bibcode:2018JAP...123b3108T. doi:10.1063/1.5003869. ISSN 0021-8979.
  9. Salvi, Jérôme; Barchiesi, Dominique (2014-04-01). "Measurement of thicknesses and optical properties of thin films from Surface Plasmon Resonance (SPR)". Applied Physics A. 115 (1): 245–255. Bibcode:2014ApPhA.115..245S. doi:10.1007/s00339-013-8038-z. ISSN 1432-0630.
  10. Özbay, E. (2006). "Plasmonics: Merging Photonics and Electronics at Nanoscale Dimensions". Science. 311 (5758): 189–93. Bibcode:2006Sci...311..189O. doi:10.1126/science.1114849. hdl:11693/38263. PMID 16410515.
  11. Akimov, Yu A; Chu, H S (2012). "Plasmon–plasmon interaction: Controlling light at nanoscale". Nanotechnology. 23 (44): 444004. doi:10.1088/0957-4484/23/44/444004. PMID 23080049.
  12. Wenshan Cai; Justin S. White & Mark L. Brongersma (2009). "Compact, High-Speed and Power-Efficient Electrooptic Plasmonic Modulators". Nano Letters. 9 (12): 4403–11. Bibcode:2009NanoL...9.4403C. doi:10.1021/nl902701b. PMID 19827771.
  13. Xu, Zhida; Chen, Yi; Gartia, Manas; Jiang, Jing; Liu, Logan (2011). "Surface plasmon enhanced broadband spectrophotometry on black silver substrates". Applied Physics Letters. 98 (24): 241904. arXiv:1402.1730. Bibcode:2011ApPhL..98x1904X. doi:10.1063/1.3599551.
  14. V. K. Valev (2012). "Characterization of Nanostructured Plasmonic Surfaces with Second Harmonic Generation". Langmuir. 28 (44): 15454–15471. doi:10.1021/la302485c. PMID 22889193.
  15. Minh Hiep, Ha; Endo, Tatsuro; Kerman, Kagan; Chikae, Miyuki; Kim, Do-Kyun; Yamamura, Shohei; Takamura, Yuzuru; Tamiya, Eiichi (2007). "A localized surface plasmon resonance based immunosensor for the detection of casein in milk". Science and Technology of Advanced Materials. 8 (4): 331. Bibcode:2007STAdM...8..331M. doi:10.1016/j.stam.2006.12.010.
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.