Tanhc function

In mathematics, the tanhc function is defined for $z\neq 0$ as[1]

\operatorname {tanhc} (z)={\frac {\tanh(z)}{z}}

The cardinal hyperbolic tangent function tanhc(z) plotted in the complex plane from -2-2i to 2+2i

The tanhc function is the hyperbolic analogue of the tanc function.

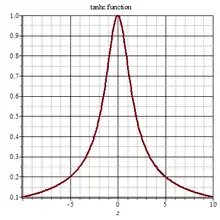
Tanhc 2D plot

Tanhc'(z) 2D plot

Tanhc integral 2D plot

Tanhc integral 3D plot

Properties

The first-order derivative is given by

{\frac {\operatorname {sech} ^{2}(z)}{z}}-{\frac {\tanh(z)}{z^{2}}}

The Taylor series expansion

\operatorname {tanhc} z\approx \left(1-{\frac {1}{3}}z^{2}+{\frac {2}{15}}z^{4}-{\frac {17}{315}}z^{6}+{\frac {62}{2835}}z^{8}-{\frac {1382}{155925}}z^{10}+{\frac {21844}{6081075}}z^{12}-{\frac {929569}{638512875}}z^{14}+O(z^{16})\right)

which leads to the series expansion of the integral as

\int _{0}^{z}\!{\frac {\tanh \left(x\right)}{x}}{dx}=(z-{\frac {1}{9}}{z}^{3}+{\frac {2}{75}}{z}^{5}-{\frac {17}{2205}}{z}^{7}+{\frac {62}{25515}}{z}^{9}-{\frac {1382}{1715175}}{z}^{11}+O\left({z}^{13}\right))

\operatorname {tanhc} \left(z\right)=\left(1+{\frac {7}{51}}\,{z}^{2}+{\frac {1}{255}}\,{z}^{4}+{\frac {2}{69615}}\,{z}^{6}+{\frac {1}{34459425}}\,{z}^{8}\right)\left(1+{\frac {8}{17}}\,{z}^{2}+{\frac {7}{255}}\,{z}^{4}+{\frac {4}{9945}}\,{z}^{6}+{\frac {1}{765765}}\,{z}^{8}\right)^{-1}

$\operatorname {tanhc} (z)=2\,{\frac {{\rm {KummerM}}\left(1,\,2,\,2\,z\right)}{(2\,iz+\pi ){\rm {KummerM}}(1,\,2,\,i\pi -2\,z)e^{2\,z-1/2\,i\pi }}}$ , where ${\rm {KummerM}}(a,b,z)$ is Kummer's confluent hypergeometric function.
$\operatorname {tanhc} (z)=2{\frac {\operatorname {HeunB} (2,0,0,0,{\sqrt {2}}{\sqrt {z}})}{(2iz+\pi )\operatorname {HeunB} (2,0,0,0,{\sqrt {2}}{\sqrt {1/2\,i\pi -z}})e^{2\,z-1/2\,i\pi }}}$ , where ${\rm {HeunB}}(q,\alpha ,\gamma ,\delta ,\epsilon ,z)$ is the biconfluent Heun function.
$\operatorname {tanhc} (z)={\frac {i{\rm {\ WhittakerM}}(0,\,1/2,\,2\,z)}{{\rm {WhittakerM}}(0,\,1/2,\,i\pi -2\,z)}}z$ , where ${\rm {WhittakerM}}(a,b,z)$ is a Whittaker function.

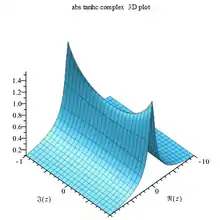Tanhc abs complex 3D

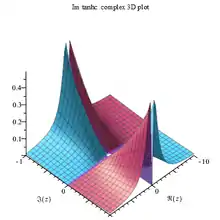Tanhc Im complex 3D plot

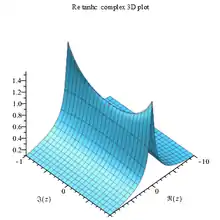Tanhc Re complex 3D plot

Tanhc'(z) Im complex 3D plot

Tanhc'(z) Re complex 3D plot

Tanhc'(z) abs complex 3D plot

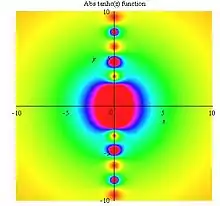Tanhc abs plot

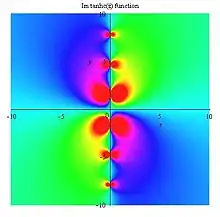Tanhc Im plot

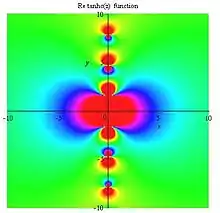Tanhc Re plot

Tanhc'(z) Im plot

Tanhc'(z) abs plot

Tanhc'(z) Re plot

Tanhc integral abs 3D plot

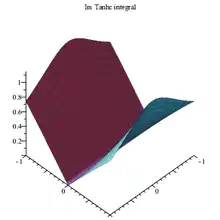Tanhc integral Im 3D plot

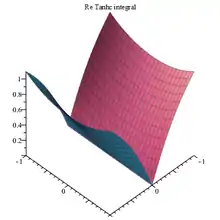Tanhc integral Re 3D plot

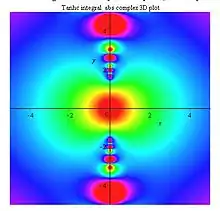Tanhc integral abs density plot

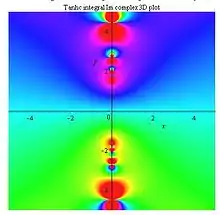Tanhc integral Im density plot

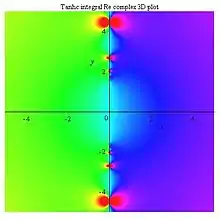Tanhc integral Re density plot

Weisstein, Eric W. "Tanhc Function". mathworld.wolfram.com. Retrieved 2022-11-17.

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.