Summation (neurophysiology)
Summation, which includes both spatial summation and temporal summation, is the process that determines whether or not an action potential will be generated by the combined effects of excitatory and inhibitory signals, both from multiple simultaneous inputs (spatial summation), and from repeated inputs (temporal summation). Depending on the sum total of many individual inputs, summation may or may not reach the threshold voltage to trigger an action potential.[1]
Neurotransmitters released from the terminals of a presynaptic neuron fall under one of two categories, depending on the ion channels gated or modulated by the neurotransmitter receptor. Excitatory neurotransmitters produce depolarization of the postsynaptic cell, whereas the hyperpolarization produced by an inhibitory neurotransmitter will mitigate the effects of an excitatory neurotransmitter.[2] This depolarization is called an EPSP, or an excitatory postsynaptic potential, and the hyperpolarization is called an IPSP, or an inhibitory postsynaptic potential.
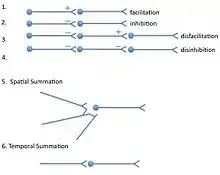
The only influences that neurons can have on one another are excitation, inhibition, and—through modulatory transmitters—biasing one another's excitability. From such a small set of basic interactions, a chain of neurons can produce only a limited response. A pathway can be facilitated by excitatory input; removal of such input constitutes disfacillitation. A pathway may also be inhibited; removal of inhibitory input constitutes disinhibition, which, if other sources of excitation are present in the inhibitory input, can augment excitation.
When a given target neuron receives inputs from multiple sources, those inputs can be spatially summated if the inputs arrive closely enough in time that the influence of the earliest-arriving inputs has not yet decayed. If a target neuron receives input from a single axon terminal and that input occurs repeatedly at short intervals, the inputs can summate temporally.
History
The nervous system first began to be encompassed within the scope of general physiological studies in the late 1800s, when Charles Sherrington began to test neurons' electrical properties. His main contributions to neurophysiology involved the study of the knee-jerk reflex and the inferences he made between the two reciprocal forces of excitation and inhibition. He postulated that the site where this modulatory response occurs is the intercellular space of a unidirectional pathway of neural circuits. He first introduced the possible role of evolution and neural inhibition with his suggestion that “higher centers of the brain inhibit the excitatory functions of the lower centers”.[1]
Much of today's knowledge of chemical synaptic transmission was gleaned from experiments analyzing the effects of acetylcholine release at neuromuscular junctions, also called end plates. The pioneers in this area included Bernard Katz and Alan Hodgkin, who used the squid giant axon as an experimental model for the study of the nervous system. The relatively large size of the neurons allowed the use of finely-tipped electrodes to monitor the electrophysiological changes that fluctuate across the membrane. In 1941 Katz's implementation of microelectrodes in the gastrocnemius sciatic nerve of frogs’ legs illuminated the field. It soon became generalized that the end-plate potential (EPP) alone is what triggers the muscle action potential, which is manifested through contractions of the frog legs.[3]
One of Katz's seminal findings, in studies carried out with Paul Fatt in 1951, was that spontaneous changes in the potential of muscle-cell membrane occur even without the stimulation of the presynaptic motor neuron. These spikes in potential are similar to action potentials except that they are much smaller, typically less than 1 mV; they were thus called miniature end plate potentials (MEPPs). In 1954, the introduction of the first electron microscopic images of postsynaptic terminals revealed that these MEPPs were created by synaptic vesicles carrying neurotransmitters. The sporadic nature of the release of quantal amounts of neurotransmitter led to the "vesicle hypothesis" of Katz and del Castillo, which attributes quantization of transmitter release to its association with synaptic vesicles.[3] This also indicated to Katz that action potential generation can be triggered by the summation of these individual units, each equivalent to an MEPP.[4]
Types
At any given moment, a neuron may receive postsynaptic potentials from thousands of other neurons. Whether threshold is reached, and an action potential generated, depends upon the spatial (i.e. from multiple neurons) and temporal (from a single neuron) summation of all inputs at that moment. It is traditionally thought that the closer a synapse is to the neuron's cell body, the greater its influence on the final summation. This is because postsynaptic potentials travel through dendrites which contain a low concentration of voltage-gated ion channels.[5] Therefore, the postsynaptic potential attenuates by the time it reaches the neuron cell body. The neuron cell body acts as a computer by integrating (adding or summing up) the incoming potentials. The net potential is then transmitted to the axon hillock, where the action potential is initiated. Another factor that should be considered is the summation of excitatory and inhibitory synaptic inputs. The spatial summation of an inhibitory input will nullify an excitatory input. This widely observed effect is called inhibitory 'shunting' of EPSPs.[5]
Spatial summation
Spatial summation is a mechanism of eliciting an action potential in a neuron with input from multiple presynaptic cells. It is the algebraic summing of potentials from different areas of input, usually on the dendrites. Summation of excitatory postsynaptic potentials increases the probability that the potential will reach the threshold potential and generate an action potential, whereas summation of inhibitory postsynaptic potentials can prevent the cell from achieving an action potential. The closer the dendritic input is to the axon hillock, the more the potential will influence the probability of the firing of an action potential in the postsynaptic cell.[6]
Temporal summation
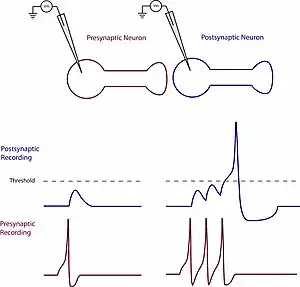
Temporal summation occurs when a high frequency of action potentials in the presynaptic neuron elicits postsynaptic potentials that summate with each other.[7] The duration of a postsynaptic potential is longer than the interval between incoming action potentials. If the time constant of the cell membrane is sufficiently long, as is the case for the cell body, then the amount of summation is increased.[6] The amplitude of one postsynaptic potential at the time point when the next one begins will algebraically summate with it, generating a larger potential than the individual potentials. This allows the membrane potential to reach the threshold to generate an action potential.[8]
Mechanism
Neurotransmitters bind to receptors which open or close ion channels in the postsynaptic cell creating postsynaptic potentials (PSPs). These potentials alter the chances of an action potential occurring in a postsynaptic neuron. PSPs are deemed excitatory if they increase the probability that an action potential will occur, and inhibitory if they decrease the chances.[4]
Glutamate as an excitatory example
The neurotransmitter glutamate, for example, is predominantly known to trigger excitatory postsynaptic potentials (EPSPs) in vertebrates. Experimental manipulation can cause the release of the glutamate through the non-tetanic stimulation of a presynaptic neuron. Glutamate then binds to AMPA receptors contained in the postsynaptic membrane causing the influx of positively charged sodium atoms.[3] This inward flow of sodium leads to a short term depolarization of the postsynaptic neuron and an EPSP. While a single depolarization of this kind may not have much of an effect on the postsynaptic neuron, repeated depolarizations caused by high frequency stimulation can lead to EPSP summation and to surpassing the threshold potential.[9]
GABA as an inhibitory example
In contrast to glutamate, the neurotransmitter GABA mainly functions to trigger inhibitory postsynaptic potentials (IPSPs) in vertebrates. The binding of GABA to a postsynaptic receptor causes the opening of ion channels that either cause an influx of negatively charged chloride ions into the cell or an efflux of positively charged potassium ions out of the cell.[3] The effect of these two options is the hyperpolarization of the postsynaptic cell, or IPSP. Summation with other IPSPs and contrasting EPSPs determines whether the postsynaptic potential will reach threshold and cause an action potential to fire in the postsynaptic neuron.
EPSP and depolarization
As long as the membrane potential is below threshold for firing impulses, the membrane potential can summate inputs. That is, if the neurotransmitter at one synapse causes a small depolarization, a simultaneous release of transmitter at another synapse located elsewhere on the same cell body will summate to cause a larger depolarization. This is called spatial summation and is complemented by temporal summation, wherein successive releases of transmitter from one synapse will cause progressive polarization change as long as the presynaptic changes occur faster than the decay rate of the membrane potential changes in the postsynaptic neuron.[4] Neurotransmitter effects last several times longer than presynaptic impulses, and thereby allow summation of effect. Thus, the EPSP differs from action potentials in a fundamental way: it summates inputs and expresses a graded response, as opposed to the all-or-none response of impulse discharge.[10]
IPSP and hyperpolarization
At the same time that a given postsynaptic neuron is receiving and summating excitatory neurotransmitter, it may also be receiving conflicting messages that are telling it to shut down firing. These inhibitory influences (IPSPs) are mediated by inhibitory neurotransmitter systems that cause postsynaptic membranes to hyperpolarize.[11] Such effects are generally attributed to the opening of selective ion channels that allow either intracellular potassium to leave the postsynaptic cell or to allow extracellular chloride to enter. In either case, the net effect is to add to the intracellular negativity and move the membrane potential farther away from the threshold for generating impulses.[8][10]
EPSPs, IPSPs, and algebraic processing
When EPSPs and IPSPs are generated simultaneously in the same cell, the output response will be determined by the relative strengths of the excitatory and inhibitory inputs. Output instructions are thus determined by this algebraic processing of information. Because the discharge threshold across a synapse is a function of the presynaptic volleys that act upon it, and because a given neuron may receive branches from many axons, the passage of impulses in a network of such synapses can be highly varied.[12] The versatility of the synapse arises from its ability to modify information by algebraically summing input signals. The subsequent change in stimulation threshold of the postsynaptic membrane can be enhanced or inhibited, depending on the transmitter chemical involved and the ion permeabilities. Thus the synapse acts as a decision point at which information converges, and it is modified by algebraic processing of EPSPs and IPSPs. In addition to the IPSP inhibitory mechanism, there is a presynaptic kind of inhibition that involves either a hyperpolarization on the inhibited axon or a persistent depolarization; whether it is the former or the latter depends on the specific neurons involved.[6]
Current research
The microelectrodes used by Katz and his contemporaries pale in comparison to the technologically advanced recording techniques available today. Spatial summation began to receive a lot of research attention when techniques were developed that allowed the simultaneous recording of multiple loci on a dendritic tree. A lot of experiments involve the use of sensory neurons, especially optical neurons, because they are constantly incorporating a ranging frequency of both inhibitory and excitatory inputs. Modern studies of neural summation focus on the attenuation of postsynaptic potentials on the dendrites and the cell body of a neuron.[1] These interactions are said to be nonlinear, because the response is less than the sum of the individual responses. Sometimes this can be due to a phenomenon caused by inhibition called shunting, which is the decreased conductance of excitatory postsynaptic potentials.[8]
Shunting inhibition is exhibited in the work of Michael Ariel and Naoki Kogo, who experimented with whole cell recording on the turtle basal optic nucleus. Their work showed that spatial summation of excitatory and inhibitory postsynaptic potentials caused attenuation of the excitatory response during the inhibitory response most of the time. They also noted a temporary augmentation of the excitatory response occurring after the attenuation. As a control they tested for attenuation when voltage-sensitive channels were activated by a hyperpolarization current. They concluded that attenuation is not caused by hyperpolarization but by an opening of synaptic receptor channels causing conductance variations.[13]
Potential therapeutic applications
Regarding nociceptive stimulation, spatial summation is the ability to integrate painful input from large areas while temporal summation refers to the ability of integrating repetitive nociceptive stimuli. Widespread and long lasting pain are characteristics of many chronic pain syndromes. This suggests that both spatial and temporal summations are important in chronic pain conditions. Indeed, through pressure stimulation experiments, it has been shown that spatial summation facilitates temporal summation of nociceptive inputs, specifically pressure pain.[14] Therefore, targeting both spatial and temporal summation mechanisms simultaneously can benefit treatment of chronic pain conditions.
References
- "temporal summation" (PDF). Athabasca University Centre for Psychology. Archived (PDF) from the original on 19 August 2011. Retrieved 29 April 2011.
- Coolen; Kuhn; Sollich (2005). Theory of Neural Information Processing Systems. London, UK: Oxford University Press.
- Bennett, Max R (2001). History of the Synapse. Australia: Hardwood Academic Publishers.
- Purves; Augustine; Fitzpatrick; Hall; LaMantia; McNamara; Williams, eds. (2008). Neuroscience. Sunderland, MA USA: Sinauer Associates Inc. OCLC 980944097.
- Kandel, ER (2013). Kandel, ER; Schwartz, JH; Jessell, TM; Siegelbaum, SA; Hudspeth, James H.; Jessell, Thomas M. (eds.). Principles of Neural Science. New York: McGraw Hill. p. 229. ISBN 9780071390118.
- Levin; Luders (2000). Comprehensive Clinical Neurophysiology. New York: W.B. Saunders Company.
- Betts, J Gordon; Desaix, Peter; Johnson, Eddie; Johnson, Jody E; Korol, Oksana; Kruse, Dean; Poe, Brandon; Wise, James; Womble, Mark D; Young, Kelly A (July 6, 2023). Anatomy & Physiology. Houston: OpenStax CNX. 12.5 Communication between neurons. ISBN 978-1-947172-04-3.
- Carpenter (1996). Neurophysiology. London: Arnold.
- Siegel, GJ; Agranoff, BW; Albers, RW, eds. (1999). Basic Neurochemistry: Molecular, Cellular and Medical Aspects. 6th edition. Philadelphia: Lippincott-Raven. Archived from the original on 2018-06-05.
- Gescheider; Wright; Verrillo (2009). Information-Processing Channels in the Tactile Sensory System. New York: Psychology Press.
- "EPSPs and IPSPs". Archived from the original on 29 December 2010. Retrieved 20 April 2011.
- Teitelbaum (1967). Physiological Psychology. New Jersey: Prentice-Hall Inc.
- Kogo; Ariel (24 November 2004). "Shunting Inhibition in Accessory Optic System Neurons". Journal of Neurophysiology. 93. doi:10.1152/jn.00214.2004.
- Nie; Graven-Nielsen; Arendt-Nielsen (July 2009). "Spatial and temporal summation of pain evoked by mechanical pressure stimulation". European Journal of Pain. 13 (6): 592–599. doi:10.1016/j.ejpain.2008.07.013. PMID 18926745. S2CID 26539019.