Cone (topology)
In topology, especially algebraic topology, the cone of a topological space is intuitively obtained by stretching X into a cylinder and then collapsing one of its end faces to a point. The cone of X is denoted by or by .
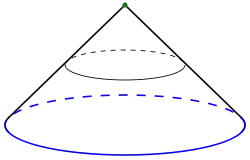
Definitions
Formally, the cone of X is defined as:
where is a point (called the vertex of the cone) and is the projection to that point. In other words, it is the result of attaching the cylinder by its face to a point along the projection .
If is a non-empty compact subspace of Euclidean space, the cone on is homeomorphic to the union of segments from to any fixed point such that these segments intersect only in itself. That is, the topological cone agrees with the geometric cone for compact spaces when the latter is defined. However, the topological cone construction is more general.
The cone is a special case of a join: the join of with a single point .[1]: 76
Examples
Here we often use a geometric cone ( where is a non-empty compact subspace of Euclidean space). The considered spaces are compact, so we get the same result up to homeomorphism.
- The cone over a point p of the real line is a line-segment in , .
- The cone over two points {0, 1} is a "V" shape with endpoints at {0} and {1}.
- The cone over a closed interval I of the real line is a filled-in triangle (with one of the edges being I), otherwise known as a 2-simplex (see the final example).
- The cone over a polygon P is a pyramid with base P.
- The cone over a disk is the solid cone of classical geometry (hence the concept's name).
- The cone over a circle given by
- is the curved surface of the solid cone:
- This in turn is homeomorphic to the closed disc.
More general examples:[1]: 77, Exercise.1
Properties
All cones are path-connected since every point can be connected to the vertex point. Furthermore, every cone is contractible to the vertex point by the homotopy
- .
The cone is used in algebraic topology precisely because it embeds a space as a subspace of a contractible space.
When X is compact and Hausdorff (essentially, when X can be embedded in Euclidean space), then the cone can be visualized as the collection of lines joining every point of X to a single point. However, this picture fails when X is not compact or not Hausdorff, as generally the quotient topology on will be finer than the set of lines joining X to a point.
Cone functor
The map induces a functor on the category of topological spaces Top. If is a continuous map, then is defined by
- ,
where square brackets denote equivalence classes.
Reduced cone
If is a pointed space, there is a related construction, the reduced cone, given by
where we take the basepoint of the reduced cone to be the equivalence class of . With this definition, the natural inclusion becomes a based map. This construction also gives a functor, from the category of pointed spaces to itself.
See also
References
- Matoušek, Jiří (2007). Using the Borsuk-Ulam Theorem: Lectures on Topological Methods in Combinatorics and Geometry (2nd ed.). Berlin-Heidelberg: Springer-Verlag. ISBN 978-3-540-00362-5.
Written in cooperation with Anders Björner and Günter M. Ziegler
, Section 4.3
- Allen Hatcher, Algebraic topology. Cambridge University Press, Cambridge, 2002. xii+544 pp. ISBN 0-521-79160-X and ISBN 0-521-79540-0
- "Cone". PlanetMath.