Total variation distance of probability measures

In probability theory, the total variation distance is a distance measure for probability distributions. It is an example of a statistical distance metric, and is sometimes called the statistical distance, statistical difference or variational distance.

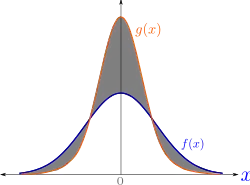
Total variation distance is half the absolute area between the two curves: Half the shaded area above.

Definition

Consider a measurable space $(\Omega ,{\mathcal {F}})$ and probability measures $P$ and $Q$ defined on $(\Omega ,{\mathcal {F}})$ . The total variation distance between $P$ and $Q$ is defined as:[1]

\delta (P,Q)=\sup _{A\in {\mathcal {F}}}\left|P(A)-Q(A)\right|.

Informally, this is the largest possible difference between the probabilities that the two probability distributions can assign to the same event.

Properties

The total variation distance is an f-divergence and an integral probability metric.

Relation to other distances

The total variation distance is related to the Kullback–Leibler divergence by Pinsker’s inequality:

\delta (P,Q)\leq {\sqrt {{\frac {1}{2}}D_{\mathrm {KL} }(P\parallel Q)}}.

One also has the following inequality, due to Bretagnolle and Huber[2] (see, also, Tsybakov[3]), which has the advantage of providing a non-vacuous bound even when $D_{\mathrm {KL} }(P\parallel Q)>2$ :

\delta (P,Q)\leq {\sqrt {1-e^{-D_{\mathrm {KL} }(P\parallel Q)}}}.

The total variation distance is half of the L¹ distance between the probability functions: on discrete domains this is the distance between probability mass functions[4] $\delta (P,Q)={\frac {1}{2}}\sum _{x}|P(x)-Q(x)|$ , The relationship holds more generally as well[5]: $\delta (P,Q)={\frac {1}{2}}\int |p(x)-q(x)|\mathrm {d} x$ when the distributions have standard probability density functions p and q, or the analogous distance between Radon-Nikodym derivatives with any common dominating measure.

The total variation distance is related to the Hellinger distance $H(P,Q)$ as follows:[6]

H^{2}(P,Q)\leq \delta (P,Q)\leq {\sqrt {2}}H(P,Q).

These inequalities follow immediately from the inequalities between the 1-norm and the 2-norm.

Connection to transportation theory

The total variation distance (or half the norm) arises as the optimal transportation cost, when the cost function is $c(x,y)={\mathbf {1} }_{x\neq y}$ , that is,

{\frac {1}{2}}\|P-Q\|_{1}=\delta (P,Q)=\inf\{\mathbb {P} (X\neq Y):{\text{Law}}(X)=P,{\text{Law}}(Y)=Q\}=\inf _{\pi }\operatorname {E} _{\pi }[{\mathbf {1} }_{x\neq y}],

where the expectation is taken with respect to the probability measure $\pi$ on the space where $(x,y)$ lives, and the infimum is taken over all such $\pi$ with marginals $P$ and $Q$ , respectively.[7]

References

Chatterjee, Sourav. "Distances between probability measures" (PDF). UC Berkeley. Archived from the original (PDF) on July 8, 2008. Retrieved 21 June 2013.
Bretagnolle, J.; Huber, C, Estimation des densités: risque minimax, Séminaire de Probabilités, XII (Univ. Strasbourg, Strasbourg, 1976/1977), pp. 342–363, Lecture Notes in Math., 649, Springer, Berlin, 1978, Lemma 2.1 (French).
Tsybakov, Alexandre B., Introduction to nonparametric estimation, Revised and extended from the 2004 French original. Translated by Vladimir Zaiats. Springer Series in Statistics. Springer, New York, 2009. xii+214 pp. ISBN 978-0-387-79051-0, Equation 2.25.
David A. Levin, Yuval Peres, Elizabeth L. Wilmer, Markov Chains and Mixing Times, 2nd. rev. ed. (AMS, 2017), Proposition 4.2, p. 48.
Tsybakov, Aleksandr B. (2009). Introduction to nonparametric estimation (rev. and extended version of the French Book ed.). New York, NY: Springer. Lemma 2.1. ISBN 978-0-387-79051-0.
Harsha, Prahladh (September 23, 2011). "Lecture notes on communication complexity" (PDF).
Villani, Cédric (2009). Optimal Transport, Old and New. Grundlehren der mathematischen Wissenschaften. Vol. 338. Springer-Verlag Berlin Heidelberg. p. 10. doi:10.1007/978-3-540-71050-9. ISBN 978-3-540-71049-3.

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.

[Chatterjee2007-1] Chatterjee, Sourav. "Distances between probability measures" (PDF). UC Berkeley. Archived from the original (PDF) on July 8, 2008. Retrieved 21 June 2013.

[2] Bretagnolle, J.; Huber, C, Estimation des densités: risque minimax, Séminaire de Probabilités, XII (Univ. Strasbourg, Strasbourg, 1976/1977), pp. 342–363, Lecture Notes in Math., 649, Springer, Berlin, 1978, Lemma 2.1 (French).

[3] Tsybakov, Alexandre B., Introduction to nonparametric estimation, Revised and extended from the 2004 French original. Translated by Vladimir Zaiats. Springer Series in Statistics. Springer, New York, 2009. xii+214 pp. ISBN 978-0-387-79051-0, Equation 2.25.

[4] David A. Levin, Yuval Peres, Elizabeth L. Wilmer, Markov Chains and Mixing Times, 2nd. rev. ed. (AMS, 2017), Proposition 4.2, p. 48.

[5] Tsybakov, Aleksandr B. (2009). Introduction to nonparametric estimation (rev. and extended version of the French Book ed.). New York, NY: Springer. Lemma 2.1. ISBN 978-0-387-79051-0.

[6] Harsha, Prahladh (September 23, 2011). "Lecture notes on communication complexity" (PDF).

[7] Villani, Cédric (2009). Optimal Transport, Old and New. Grundlehren der mathematischen Wissenschaften. Vol. 338. Springer-Verlag Berlin Heidelberg. p. 10. doi:10.1007/978-3-540-71050-9. ISBN 978-3-540-71049-3.