Transcendental equation
In applied mathematics, a transcendental equation is an equation over the real (or complex) numbers that is not algebraic, that is, if at least one of its sides describes a transcendental function.[1] Examples include:

A transcendental equation need not be an equation between elementary functions, although most published examples are.
In some cases, a transcendental equation can be solved by transforming it into an equivalent algebraic equation. Some such transformations are sketched below; computer algebra systems may provide more elaborated transformations.[lower-alpha 1]
In general, however, only approximate solutions can be found.[2]
Transformation into an algebraic equation
Ad hoc methods exist for some classes of transcendental equations in one variable to transform them into algebraic equations which then might be solved.
Exponential equations
If the unknown, say x, occurs only in exponents:
- applying the natural logarithm to both sides may yield an algebraic equation,[3] e.g.
- transforms to , which simplifies to , which has the solutions
- This will not work if addition occurs "at the base line", as in
- if all "base constants" can be written as integer or rational powers of some number q, then substituting y=qx may succeed, e.g.
- transforms, using y=2x, to which has the solutions , hence is the only real solution.[4]
- This will not work if squares or higher power of x occurs in an exponent, or if the "base constants" do not "share" a common q.
- sometimes, substituting y=xex may obtain an algebraic equation; after the solutions for y are known, those for x can be obtained by applying the Lambert W function, e.g.:
- transforms to which has the solutions hence , where and the denote the real-valued branches of the multivalued function.
Logarithmic equations
If the unknown x occurs only in arguments of a logarithm function:
- applying exponentiation to both sides may yield an algebraic equation, e.g.
- transforms, using exponentiation to base to which has the solutions If only real numbers are considered, is not a solution, as it leads to a non-real subexpression in the given equation.
- This requires the original equation to consist of integer-coefficient linear combinations of logarithms w.r.t. a unique base, and the logarithm arguments to be polynomials in x.[5]
- if all "logarithm calls" have a unique base and a unique argument expression then substituting may lead to a simpler equation,[6] e.g.
- transforms, using to which is algebraic and has the single solution .[lower-alpha 2] After that, applying inverse operations to the substitution equation yields
Trigonometric equations
If the unknown x occurs only as argument of trigonometric functions:
- applying Pythagorean identities and trigonometric sum and multiple formulas, arguments of the forms with integer might all be transformed to arguments of the form, say, . After that, substituting yields an algebraic equation,[7] e.g.
- transforms to , and, after substitution, to which is algebraic[lower-alpha 3] and can be solved. After that, applying obtains the solutions.
Hyperbolic equations
If the unknown x occurs only in linear expressions inside arguments of hyperbolic functions,
- unfolding them by their defining exponential expressions and substituting yields an algebraic equation,[8] e.g.
- unfolds to which transforms to the equation which is algebraic[lower-alpha 4] and can be solved. Applying obtains the solutions of the original equation.
Approximate solutions
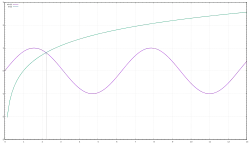
Approximate numerical solutions to transcendental equations can be found using numerical, analytical approximations, or graphical methods.
Numerical methods for solving arbitrary equations are called root-finding algorithms.
In some cases, the equation can be well approximated using Taylor series near the zero. For example, for , the solutions of are approximately those of , namely and .
For a graphical solution, one method is to set each side of a single-variable transcendental equation equal to a dependent variable and plot the two graphs, using their intersecting points to find solutions (see picture).
Other solutions
- Some transcendental systems of high-order equations can be solved by “separation” of the unknowns, reducing them to algebraic equations.[9][10]
- The following can also be used when solving transcendental equations/inequalities: If is a solution to the equation and , then this solution must satisfy . For example, we want to solve . The given equation is defined for . Let and . It is easy to show that and so if there is a solution to the equation, it must satisfy . From we get . Indeed, and so is the only real solution to the equation.
See also
- Mrs. Miniver's problem – Problem on areas of intersecting circles
Notes
- For example, according to the Wolfram Mathematica tutorial page on equation solving, both and can be solved by symbolic expressions, while can only be solved approximatively.
- Squaring both sides obtains which has the additional solution ; however, the latter does not solve the unsquared equation.
- over an appropriate field, containing and
- over an appropriate field, containing
References
- I.N. Bronstein and K.A. Semendjajew and G. Musiol and H. Mühlig (2005). Taschenbuch der Mathematik (in German). Frankfurt/Main: Harri Deutsch. Here: Sect.1.6.4.1, p.45. The domain of equations is left implicit throughout the book.
- Bronstein et al., p.45-46
- Bronstein et al., Sect.1.6.4.2.a, p.46
- Bronstein et al., Sect.1.6.4.2.b, p.46
- Bronstein et al., Sect.1.6.4.3.b, p.46
- Bronstein et al., Sect.1.6.4.3.a, p.46
- Bronstein et al., Sect.1.6.4.4, p.46-47
- Bronstein et al., Sect.1.6.4.5, p.47
- V. A. Varyuhin, S. A. Kas'yanyuk, “On a certain method for solving nonlinear systems of a special type”, Zh. Vychisl. Mat. Mat. Fiz., 6:2 (1966), 347–352; U.S.S.R. Comput. Math. Math. Phys., 6:2 (1966), 214–221
- V.A. Varyukhin, Fundamental Theory of Multichannel Analysis (VA PVO SV, Kyiv, 1993) [in Russian]
- John P. Boyd (2014). Solving Transcendental Equations: The Chebyshev Polynomial Proxy and Other Numerical Rootfinders, Perturbation Series, and Oracles. Other Titles in Applied Mathematics. Philadelphia: Society for Industrial and Applied Mathematics (SIAM). doi:10.1137/1.9781611973525. ISBN 978-1-61197-351-8.