Trigonal trapezohedral honeycomb

In geometry, the trigonal trapezohedral honeycomb is a uniform space-filling tessellation (or honeycomb) in Euclidean 3-space. Cells are identical trigonal trapezohedra or rhombohedra. Conway, Burgiel, and Goodman-Strauss call it an oblate cubille.[1]

Trigonal trapezohedral honeycomb
(No image)
TypeDual uniform honeycomb
Coxeter-Dynkin diagrams
Cell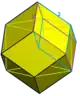
Trigonal trapezohedron
(1/4 of rhombic dodecahedron)
Faces Rhombus
Space groupFd3m (227)
Coxeter group×2, 3[4] (double)
vertex figures
|
DualQuarter cubic honeycomb
PropertiesCell-transitive, Face-transitive

This honeycomb can be seen as a rhombic dodecahedral honeycomb, with the rhombic dodecahedra dissected with its center into 4 trigonal trapezohedra or rhombohedra.


rhombic dodecahedral honeycomb
Rhombic dodecahedra dissection
Rhombic net

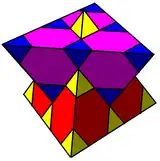
It is analogous to the regular hexagonal being dissectable into 3 rhombi and tiling the plane as a rhombille. The rhombille tiling is actually an orthogonal projection of the trigonal trapezohedral honeycomb. A different orthogonal projection produces the quadrille where the rhombi are distorted into squares.

Dual tiling

It is dual to the quarter cubic honeycomb with tetrahedral and truncated tetrahedral cells:

See also

References
  1. Conway, John H.; Burgiel, Heidi; Goodman-Strauss, Chaim (2008), The Symmetries of Things, Wellesley, Massachusetts: A K Peters, p. 294, ISBN 978-1-56881-220-5, MR 2410150
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.