Trisected perimeter point
In geometry, given a triangle ABC, there exist unique points A´, B´, and C´ on the sides BC, CA, AB respectively, such that:[1]
- A´, B´, and C´ partition the perimeter of the triangle into three equal-length pieces. That is,
- C´B + BA´ = B´A + AC´ = A´C + CB´.
- The three lines AA´, BB´, and CC´ meet in a point, the trisected perimeter point.
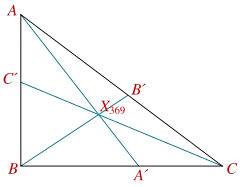
The trisected perimeter point of a 3-4-5 right triangle. For this triangle, C´B = A´C and BA´ = CB´, but that is not the case for triangles of other shapes.
This is point X369 in Clark Kimberling's Encyclopedia of Triangle Centers.[2] Uniqueness and a formula for the trilinear coordinates of X369 were shown by Peter Yff late in the twentieth century. The formula involves the unique real root of a cubic equation.[2]
See also
References
- Weisstein, Eric W. "Trisected Perimeter Point". MathWorld.
- Kimberling, C. Encyclopedia of Triangle Centers. X(369) = 1st TRISECTED PERIMETER POINT.
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.