Turing pattern
The Turing pattern is a concept introduced by English mathematician Alan Turing in a 1952 paper titled "The Chemical Basis of Morphogenesis" which describes how patterns in nature, such as stripes and spots, can arise naturally and autonomously from a homogeneous, uniform state.[1][2] The pattern arises due to Turing instability which in turn arises due to the interplay between differential diffusion (i.e., different values of diffusion coefficients) of chemical species and chemical reaction. The instability mechanism is unforeseen because a pure diffusion process would be anticipated to have a stabilizing influence on the system.

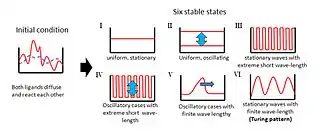
Overview
In his paper,[1] Turing examined the behaviour of a system in which two diffusible substances interact with each other, and found that such a system is able to generate a spatially periodic pattern even from a random or almost uniform initial condition.[3] Prior to the discovery of this instability mechanism arising due to unequal diffusion coefficients of the two substances, diffusional effects were always presumed to have stabilizing influences on the system.
Turing hypothesized that the resulting wavelike patterns are the chemical basis of morphogenesis.[3] Turing patterning is often found in combination with other patterns: vertebrate limb development is one of the many phenotypes exhibiting Turing patterning overlapped with a complementary pattern (in this case a French flag model).[4]
Before Turing, Yakov Zeldovich in 1944 discovered this instability mechanism in connection with the cellular structures observed in lean hydrogen flames.[5] Zeldovich explained the cellular structure as a consequence of hydrogen's diffusion coefficient being larger than the thermal diffusion coefficient. In combustion literature, Turing instability is referred to as diffusive–thermal instability.
Concept
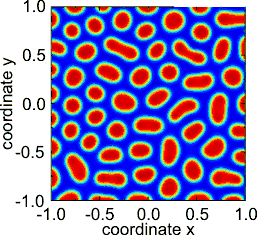

The original theory, a reaction–diffusion theory of morphogenesis, has served as an important model in theoretical biology.[6] Reaction–diffusion systems have attracted much interest as a prototype model for pattern formation. Patterns such as fronts, hexagons, spirals, stripes and dissipative solitons are found as solutions of Turing-like reaction–diffusion equations.[7]
Turing proposed a model wherein two homogeneously distributed substances (P and S) interact to produce stable patterns during morphogenesis. These patterns represent regional differences in the concentrations of the two substances. Their interactions would produce an ordered structure out of random chaos.[8]
In Turing's model, substance P promotes the production of more substance P as well as substance S. However, substance S inhibits the production of substance P; if S diffuses more readily than P, sharp waves of concentration differences will be generated for substance P. An important feature of Turing´s model is that particular wavelengths in the substances' distribution will be amplified while other wavelengths will be suppressed.[8]
The parameters depend on the physical system under consideration. In the context of fish skin pigmentation, the associated equation is a three field reaction–diffusion one in which the linear parameters are associated with pigmentation cell concentration and the diffusion parameters are not the same for all fields.[9] In dye-doped liquid crystals, a photoisomerization process in the liquid crystal matrix is described as a reaction–diffusion equation of two fields (liquid crystal order parameter and concentration of cis-isomer of the azo-dye).[10] The systems have very different physical mechanisms on the chemical reactions and diffusive process, but on a phenomenological level, both have the same ingredients.
Turing-like patterns have also been demonstrated to arise in developing organisms without the classical requirement of diffusible morphogens. Studies in chick and mouse embryonic development suggest that the patterns of feather and hair-follicle precursors can be formed without a morphogen pre-pattern, and instead are generated through self-aggregation of mesenchymal cells underlying the skin.[11][12] In these cases, a uniform population of cells can form regularly patterned aggregates that depend on the mechanical properties of the cells themselves and the rigidity of the surrounding extra-cellular environment. Regular patterns of cell aggregates of this sort were originally proposed in a theoretical model formulated by George Oster, which postulated that alterations in cellular motility and stiffness could give rise to different self-emergent patterns from a uniform field of cells.[13] This mode of pattern formation may act in tandem with classical reaction-diffusion systems, or independently to generate patterns in biological development.
Turing patterns may also be responsible for the formation of human fingerprints.[14]
As well as in biological organisms, Turing patterns occur in other natural systems – for example, the wind patterns formed in sand, the atomic-scale repetitive ripples that can form during growth of bismuth crystals, and the uneven distribution of matter in galactic disc.[15][16] Although Turing's ideas on morphogenesis and Turing patterns remained dormant for many years, they are now inspirational for much research in mathematical biology.[17] It is a major theory in developmental biology; the importance of the Turing model is obvious, as it provides an answer to the fundamental question of morphogenesis: “how is spatial information generated in organisms?”.[3]
Turing patterns can also be created in nonlinear optics as demonstrated by the Lugiato–Lefever equation.
Biological application
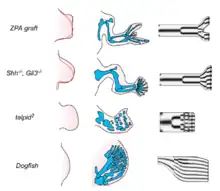
A mechanism that has gained increasing attention as a generator of spot- and stripe-like patterns in developmental systems is related to the chemical reaction-diffusion process described by Turing in 1952. This has been schematized in a biological "local autoactivation-lateral inhibition" (LALI) framework by Meinhardt and Gierer.[19] LALI systems, while formally similar to reaction-diffusion systems, are more suitable to biological applications, since they include cases where the activator and inhibitor terms are mediated by cellular ‘‘reactors’’ rather than simple chemical reactions,[20] and spatial transport can be mediated by mechanisms in addition to simple diffusion.[21] These models can be applied to limb formation and teeth development among other examples.
Reaction-diffusion models can be used to forecast the exact location of the tooth cusps in mice and voles based on differences in gene expression patterns.[8] The model can be used to explain the differences in gene expression between mice and vole teeth, the signaling center of the tooth, enamel knot, secrets BMPs, FGFs and Shh. Shh and FGF inhibits BMP production, while BMP stimulates both the production of more BMPs and the synthesis of their own inhibitors. BMPs also induce epithelial differentiation, while FGFs induce epithelial growth.[22] The result is a pattern of gene activity that changes as the shape of the tooth changes, and vice versa. Under this model, the large differences between mouse and vole molars can be generated by small changes in the binding constants and diffusion rates of the BMP and Shh proteins. A small increase in the diffusion rate of BMP4 and a stronger binding constant of its inhibitor is sufficient to change the vole pattern of tooth growth into that of the mouse.[22][23]
Experiments with the sprouting of chia seeds planted in trays have confirmed Turing's mathematical model.[24]
See also
References
- Turing, Alan (1952). "The Chemical Basis of Morphogenesis" (PDF). Philosophical Transactions of the Royal Society of London B. 237 (641): 37–72. Bibcode:1952RSPTB.237...37T. doi:10.1098/rstb.1952.0012. JSTOR 92463. S2CID 120437796.
- Stewart, Ian (1998). Life's Other Secret: The New Mathematics of the Living World. Allen Lane: The Penguin Press. pp. 138–140, 142–146, 148, 149, 151, 152. ISBN 0-713-99161-5.
- Kondo, Shigeru (7 February 2017). "An updated kernel-based Turing model for studying the mechanisms of biological pattern formation". Journal of Theoretical Biology. 414: 120–127. Bibcode:2017JThBi.414..120K. doi:10.1016/j.jtbi.2016.11.003. ISSN 0022-5193. PMID 27838459.
- Sharpe, James; Green, Jeremy (2015). "Positional information and reaction-diffusion: two big ideas in developmental biology combine". Development. 142 (7): 1203–1211. doi:10.1242/dev.114991. PMID 25804733.
- Zeldovich, Y. B. (1944). Theory of Combustion and Detonation of Gases. Selected Works of Yakov Borisovich Zeldovich, Volume I: Chemical Physics and Hydrodynamics (pp. 162-232). Princeton: Princeton University Press
- Harrison, L. G. (1993). "Kinetic Theory of Living Pattern". Endeavour. Cambridge University Press. 18 (4): 130–6. doi:10.1016/0160-9327(95)90520-5. PMID 7851310.
- Kondo, S.; Miura, T. (23 September 2010). "Reaction-Diffusion Model as a Framework for Understanding Biological Pattern Formation". Science. 329 (5999): 1616–1620. Bibcode:2010Sci...329.1616K. doi:10.1126/science.1179047. PMID 20929839. S2CID 10194433.
- Gilbert, Scott F., 1949- (2014). Developmental biology (Tenth ed.). Sunderland, MA, USA. ISBN 978-0-87893-978-7. OCLC 837923468.
{{cite book}}: CS1 maint: location missing publisher (link) CS1 maint: multiple names: authors list (link) - Nakamasu, A.; Takahashi, G.; Kanbe, A.; Kondo, S. (11 May 2009). "Interactions between zebrafish pigment cells responsible for the generation of Turing patterns". Proceedings of the National Academy of Sciences. 106 (21): 8429–8434. Bibcode:2009PNAS..106.8429N. doi:10.1073/pnas.0808622106. PMC 2689028. PMID 19433782.
- Andrade-Silva, Ignacio; Bortolozzo, Umberto; Clerc, Marcel G.; González-Cortés, Gregorio; Residori, Stefania; Wilson, Mario (27 August 2018). "Spontaneous light-induced Turing patterns in a dye-doped twisted nematic layer". Scientific Reports. 8 (1): 12867. Bibcode:2018NatSR...812867A. doi:10.1038/s41598-018-31206-x. PMC 6110868. PMID 30150701.
- Glover, James D.; Wells, Kirsty L.; Matthäus, Franziska; Painter, Kevin J.; Ho, William; Riddell, Jon; Johansson, Jeanette A.; Ford, Matthew J.; Jahoda, Colin A. B.; Klika, Vaclav; Mort, Richard L. (2017). "Hierarchical patterning modes orchestrate hair follicle morphogenesis". PLOS Biology. 15 (7): e2002117. doi:10.1371/journal.pbio.2002117. PMC 5507405. PMID 28700594.
- Shyer, Amy E.; Rodrigues, Alan R.; Schroeder, Grant G.; Kassianidou, Elena; Kumar, Sanjay; Harland, Richard M. (2017). "Emergent cellular self-organization and mechanosensation initiate follicle pattern in the avian skin". Science. 357 (6353): 811–815. doi:10.1126/science.aai7868. PMC 5605277. PMID 28705989.
- Oster, G. F.; Murray, J. D.; Harris, A. K. (1983). "Mechanical aspects of mesenchymal morphogenesis". Journal of Embryology and Experimental Morphology. 78: 83–125. PMID 6663234.
- Gaines, James M. "Finally, Scientists Uncover the Genetic Basis of Fingerprints". TheScientist. Retrieved 27 February 2023.
- Fuseya, Yuki; Katsuno, Hiroyasu; Behnia, Kamran; Kapitulnik, Aharon (8 July 2021). "Nanoscale Turing patterns in a bismuth monolayer". Nature Physics. 17 (9): 1031–1036. arXiv:2104.01058. Bibcode:2021NatPh..17.1031F. doi:10.1038/s41567-021-01288-y. ISSN 1745-2481. S2CID 237767233.
- Smolin, Lee (3 December 1996). "Galactic disks as reaction-diffusion systems". arXiv:astro-ph/9612033.
- Woolley, T. E., Baker, R. E., Maini, P. K., Chapter 34, Turing's theory of morphogenesis. In Copeland, B. Jack; Bowen, Jonathan P.; Wilson, Robin; Sprevak, Mark (2017). The Turing Guide. Oxford University Press. ISBN 978-0198747826.
- Zhu, Jianfeng; Zhang, Yong-Tao; Alber, Mark S.; Newman, Stuart A. (28 May 2010). Isalan, Mark (ed.). "Bare Bones Pattern Formation: A Core Regulatory Network in Varying Geometries Reproduces Major Features of Vertebrate Limb Development and Evolution". PLOS ONE. 5 (5): e10892. Bibcode:2010PLoSO...510892Z. doi:10.1371/journal.pone.0010892. ISSN 1932-6203. PMC 2878345. PMID 20531940.
- Meinhardt, Hans (2008), "Models of Biological Pattern Formation: From Elementary Steps to the Organization of Embryonic Axes", Multiscale Modeling of Developmental Systems, Current Topics in Developmental Biology, vol. 81, Elsevier, pp. 1–63, doi:10.1016/s0070-2153(07)81001-5, ISBN 978-0-12-374253-7, PMID 18023723
- Hentschel, H. G. E.; Glimm, Tilmann; Glazier, James A.; Newman, Stuart A. (22 August 2004). "Dynamical mechanisms for skeletal pattern formation in the vertebrate limb". Proceedings of the Royal Society of London. Series B: Biological Sciences. 271 (1549): 1713–1722. doi:10.1098/rspb.2004.2772. ISSN 0962-8452. PMC 1691788. PMID 15306292.
- Lander, Arthur D. (January 2007). "Morpheus Unbound: Reimagining the Morphogen Gradient". Cell. 128 (2): 245–256. doi:10.1016/j.cell.2007.01.004. ISSN 0092-8674. PMID 17254964. S2CID 14173945.
- Salazar-Ciudad, Isaac; Jernvall, Jukka (March 2010). "A computational model of teeth and the developmental origins of morphological variation". Nature. 464 (7288): 583–586. Bibcode:2010Natur.464..583S. doi:10.1038/nature08838. ISSN 1476-4687. PMID 20220757. S2CID 323733.
- Salazar-ciudad, Isaac; Jernvall, Jukka (January 2004). "How different types of pattern formation mechanisms affect the evolution of form and development". Evolution and Development. 6 (1): 6–16. doi:10.1111/j.1525-142x.2004.04002.x. ISSN 1520-541X. PMID 15108813. S2CID 1783730.
- Riordon, James R. (26 March 2023). "Chia seedlings verify Alan Turing's ideas about patterns in nature". ScienceNews.
Further reading
- Ball, Philip (31 May 2012). "Turing Patterns". Chemistry World. (See also extended version, June 2012.)
- Campagna, R.; Cuomo, S.; Giannino, F.; Severino, G.; Toraldo, G. (6 December 2017). "A semi-automatic numerical algorithm for Turing patterns formation in a reaction-diffusion model". IEEE Access. 6: 4720–4724. doi:10.1109/ACCESS.2017.2780324.
- Iber, Bagnar. "Turing Pattern" (PDF). Computational Biology (CoBI). Switzerland: ETH Zurich. Retrieved 16 August 2018.
- Keim, Brandon (22 February 2011). "Alan Turing's Patterns in Nature and Beyond". Wired.
- Ouellette, Jennifer (27 March 2013). "When Math Meets Nature: Turing Patterns and Form Constants". Scientific American.