Tutte theorem

In the mathematical discipline of graph theory the Tutte theorem, named after William Thomas Tutte, is a characterization of finite undirected graphs with perfect matchings. It is a generalization of Hall's marriage theorem from bipartite to arbitrary graphs. It is a special case of the Tutte–Berge formula.

Example of a graph and one of its perfect matchings (in red).

Intuition

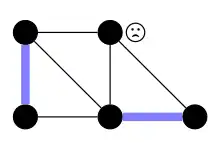
An graph (or a component) with an odd number of vertices cannot have a perfect matching, since there will always be a vertex left alone.

The goal is to characterize all graphs that do not have a perfect matching. Start with the most obvious case of a graph without a perfect matching: a graph with an odd number of vertices. In such a graph, any matching leaves at least one unmatched vertex, so it cannot be perfect.

A slightly more general case is a disconnected graph in which one or more components have an odd number of vertices (even if the total number of vertices is even). Let us call such components odd components. In any matching, each vertex can only be matched to vertices in the same component. Therefore, any matching leaves at least one unmatched vertex in every odd component, so it cannot be perfect.

Next, consider a graph G with a vertex u such that, if we remove from G the vertex u and its adjacent edges, the remaining graph (denoted $G - u$ ) has two or more odd components. As above, any matching leaves, in every odd component, at least one vertex that is unmatched to other vertices in the same component. Such a vertex can only be matched to u. But since there are two or more unmatched vertices, and only one of them can be matched to u, at least one other vertex remains unmatched, so the matching is not perfect.

Finally, consider a graph G with a set of vertices $U$ such that, if we remove from G the vertices in $U$ and all edges adjacent to them, the remaining graph (denoted $G - U$ ) has more than $| U |$ odd components. As explained above, any matching leaves at least one unmatched vertex in every odd component, and these can be matched only to vertices of $U$ - but there are not enough vertices on $U$ for all these unmatched vertices, so the matching is not perfect.

We have arrived at a necessary condition: if G has a perfect matching, then for every vertex subset $U$ in G, the graph $G - U$ has at most $| U |$ odd components. Tutte's theorem says that this condition is both necessary and sufficient for the existence of perfect matching.

Tutte's theorem

A graph, $G = (V, E)$ , has a perfect matching if and only if for every subset $U$ of $V$ , the subgraph $G - U$ has at most $| U |$ odd components (connected components having an odd number of vertices).[1]

Proof

First we write the condition:

(*)\qquad \forall U\subseteq V,\quad odd(G-U)\leq |U|

where $odd(X)$ denotes the number of odd components of the subgraph induced by $X$ .

Necessity of (∗): This direction was already discussed in the section Intuition below, but let us sum up here the proof. Consider a graph $G$ , with a perfect matching. Let $U$ be an arbitrary subset of $V$ . Delete $U$ . Let $C$ be an arbitrary odd component in $G - U$ . Since $G$ had a perfect matching, at least one vertex in $C$ must be matched to a vertex in $U$ . Hence, each odd component has at least one vertex matched with a vertex in $U$ . Since each vertex in $U$ can be in this relation with at most one connected component (because of it being matched at most once in a perfect matching), $odd (G - U) \leq | U |$ .[2]

Sufficiency of (∗): Let $G$ be an arbitrary graph with no perfect matching. We will find a so-called Tutte violator, that is, a subset $S$ of $V$ such that $| S | < odd (G - S)$ . We can suppose that $G$ is edge-maximal, i.e., $G + e$ has a perfect matching for every edge $e$ not present in $G$ already. Indeed, if we find a Tutte violator $S$ in edge-maximal graph $G$ , then $S$ is also a Tutte violator in every spanning subgraph of $G$ , as every odd component of $G - S$ will be split into possibly more components at least one of which will again be odd.

We define $S$ to be the set of vertices with degree $| V | - 1$ . First we consider the case where all components of $G - S$ are complete graphs. Then $S$ has to be a Tutte violator, since if $odd (G - S) \leq | S |$ , then we could find a perfect matching by matching one vertex from every odd component with a vertex from $S$ and pairing up all other vertices (this will work unless $| V |$ is odd, but then $\emptyset$ is a Tutte violator).

Now suppose that $K$ is a component of $G - S$ and $x, y \in K$ are vertices such that $xy \notin E$ . Let $x, a, b \in K$ be the first vertices on a shortest $x, y$ -path in $K$ . This ensures that $xa, ab \in E$ and $xb \notin E$ . Since $a \notin S$ , there exists a vertex $c$ such that $ac \notin E$ . From the edge-maximality of $G$ , we define $M 1$ as a perfect matching in $G + xb$ and $M 2$ as a perfect matching in $G + ac$ . Observe that surely $xb \in M 1$ and $ac \in M 2$ .

Let $P$ be the maximal path in $G$ that starts from $c$ with an edge from $M 1$ and whose edges alternate between $M 1$ and $M 2$ . How can $P$ end? Unless we arrive at 'special' vertex such as $x, a$ or $b$ , we can always continue: $c$ is $M 2$ -matched by $ca$ , so the first edge of $P$ is not in $M 2$ , therefore the second vertex is $M 2$ -matched by a different edge and we continue in this manner.

Let $v$ denote the last vertex of $P$ . If the last edge of $P$ is in $M 1$ , then $v$ has to be $a$ , since otherwise we could continue with an edge from $M 2$ (even to arrive at $x$ or $b$ ). In this case we define $C := P + ac$ . If the last edge of $P$ is in $M 2$ , then surely $v \in {x, b$ } for analogous reason and we define $C := P + va + ac$ .

Now $C$ is a cycle in $G + ac$ of even length with every other edge in $M 2$ . We can now define $M := M 2 Δ C$ (where $Δ$ is symmetric difference) and we obtain a perfect matching in $G$ , a contradiction.

Equivalence to the Tutte-Berge formula

The Tutte–Berge formula says that the size of a maximum matching of a graph $G=(V,E)$ equals $\min _{U\subseteq V}\left(|U|-\operatorname {odd} (G-U)+|V|\right)/2$ . Equivalently, the number of unmatched vertices in a maximum matching equals $\max _{U\subseteq V}\left(\operatorname {odd} (G-U)-|U|\right)$ .

This formula follows from Tutte's theorem, together with the observation that $G$ has a matching of size $k$ if and only if the graph $G^{(k)}$ obtained by adding $|V|-2k$ new vertices, each joined to every original vertex of $G$ , has a perfect matching. Since any set $X$ which separates $G^{(k)}$ into more than $|X|$ components must contain all the new vertices, (*) is satisfied for $G^{(k)}$ if and only if $k\leq \min _{U\subseteq V}\left(|U|-\operatorname {odd} (G-U)+|V|\right)/2$ .

In infinite graphs

For connected infinite graphs that are locally finite (every vertex has finite degree), a generalization of Tutte's condition holds: such graphs have perfect matchings if and only if there is no finite subset, the removal of which creates a number of finite odd components larger than the size of the subset.[3]

Notes

Lovász & Plummer (1986), p. 84; Bondy & Murty (1976), Theorem 5.4, p. 76.
Bondy & Murty (1976), pp. 76–78.
Tutte, W. T. (1950). "The factorization of locally finite graphs". Canadian Journal of Mathematics. 2: 44–49. doi:10.4153/cjm-1950-005-2. MR 0032986. S2CID 124434131.

References

Bondy, J. A.; Murty, U. S. R. (1976). Graph theory with applications. New York: American Elsevier Pub. Co. ISBN 0-444-19451-7.
Lovász, László; Plummer, M. D. (1986). Matching theory. Amsterdam: North-Holland. ISBN 0-444-87916-1.

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.

[1] Lovász & Plummer (1986), p. 84; Bondy & Murty (1976), Theorem 5.4, p. 76.

[bm-proof-2] Bondy & Murty (1976), pp. 76–78.

[3] Tutte, W. T. (1950). "The factorization of locally finite graphs". Canadian Journal of Mathematics. 2: 44–49. doi:10.4153/cjm-1950-005-2. MR 0032986. S2CID 124434131.