Ultragraph C*-algebra
In mathematics, an ultragraph C*-algebra is a universal C*-algebra generated by partial isometries on a collection of Hilbert spaces constructed from ultragraphs.[1]pp. 6-7. These C*-algebras were created in order to simultaneously generalize the classes of graph C*-algebras and Exel–Laca algebras, giving a unified framework for studying these objects.[1] This is because every graph can be encoded as an ultragraph, and similarly, every infinite graph giving an Exel-Laca algebras can also be encoded as an ultragraph.
Definitions
Ultragraphs
An ultragraph consists of a set of vertices , a set of edges , a source map , and a range map taking values in the power set collection of nonempty subsets of the vertex set. A directed graph is the special case of an ultragraph in which the range of each edge is a singleton, and ultragraphs may be thought of as generalized directed graph in which each edges starts at a single vertex and points to a nonempty subset of vertices.
Example
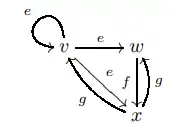
An easy way to visualize an ultragraph is to consider a directed graph with a set of labelled vertices, where each label corresponds to a subset in the image of an element of the range map. For example, given an ultragraph with vertices and edge labels
,
with source an range maps
can be visualized as the image on the right.
Ultragraph algebras
Given an ultragraph , we define to be the smallest subset of containing the singleton sets , containing the range sets , and closed under intersections, unions, and relative complements. A Cuntz–Krieger -family is a collection of projections together with a collection of partial isometries with mutually orthogonal ranges satisfying
- , , for all ,
- for all ,
- whenever is a vertex that emits a finite number of edges, and
- for all .
The ultragraph C*-algebra is the universal C*-algebra generated by a Cuntz–Krieger -family.
Properties
Every graph C*-algebra is seen to be an ultragraph algebra by simply considering the graph as a special case of an ultragraph, and realizing that is the collection of all finite subsets of and for each . Every Exel–Laca algebras is also an ultragraph C*-algebra: If is an infinite square matrix with index set and entries in , one can define an ultragraph by , , , and . It can be shown that is isomorphic to the Exel–Laca algebra .[1]
Ultragraph C*-algebras are useful tools for studying both graph C*-algebras and Exel–Laca algebras. Among other benefits, modeling an Exel–Laca algebra as ultragraph C*-algebra allows one to use the ultragraph as a tool to study the associated C*-algebras, thereby providing the option to use graph-theoretic techniques, rather than matrix techniques, when studying the Exel–Laca algebra. Ultragraph C*-algebras have been used to show that every simple AF-algebra is isomorphic to either a graph C*-algebra or an Exel–Laca algebra.[2] They have also been used to prove that every AF-algebra with no (nonzero) finite-dimensional quotient is isomorphic to an Exel–Laca algebra.[2]
While the classes of graph C*-algebras, Exel–Laca algebras, and ultragraph C*-algebras each contain C*-algebras not isomorphic to any C*-algebra in the other two classes, the three classes have been shown to coincide up to Morita equivalence.[3]
See also
- Leavitt path algebra
- Exel–Laca algebras
- Infinite matrix
- Infinite graph
Notes
- A unified approach to Exel–Laca algebras and C*-algebras associated to graphs, Mark Tomforde, J. Operator Theory 50 (2003), no. 2, 345–368.
- Realization of AF-algebras as graph algebras, Exel–Laca algebras, and ultragraph algebras, Takeshi Katsura, Aidan Sims, and Mark Tomforde, J. Funct. Anal. 257 (2009), no. 5, 1589–1620.
- Graph algebras, Exel–Laca algebras, and ultragraph algebras coincide up to Morita equivalence, Takeshi Katsura, Paul Muhly, Aidan Sims, and Mark Tomforde, J. Reine Angew. Math. 640 (2010), 135–165.