WAVL tree

In computer science, a WAVL tree or weak AVL tree is a self-balancing binary search tree. WAVL trees are named after AVL trees, another type of balanced search tree, and are closely related both to AVL trees and red–black trees, which all fall into a common framework of rank balanced trees. Like other balanced binary search trees, WAVL trees can handle insertion, deletion, and search operations in time $O (log n)$ per operation.[1][2]

WAVL trees are designed to combine some of the best properties of both AVL trees and red–black trees. One advantage of AVL trees over red–black trees is being more balanced: they have height at most $\log _{\varphi }n\approx 1.44\log _{2}n$ (for a tree with $n$ data items, where $\varphi$ is the golden ratio), while red–black trees have larger maximum height, $2\log _{2}n$ . If a WAVL tree is created using only insertions, without deletions, then it has the same small height bound that an AVL tree has. On the other hand, red–black trees have the advantage over AVL trees in lesser restructuring of their trees. In AVL trees, each deletion may require a logarithmic number of tree rotation operations, while red–black trees have simpler deletion operations that use only a constant number of tree rotations. WAVL trees, like red–black trees, use only a constant number of tree rotations, and the constant is even better than for red–black trees.[1][2]

WAVL trees were introduced by Haeupler, Sen & Tarjan (2015). The same authors also provided a common view of AVL trees, WAVL trees, and red–black trees as all being a type of rank-balanced tree.[2]

The rank balanced trees framework

Different binary search trees have different algorithms for insert/delete and balancing algorithms, making it difficult for a systematic study. The authors of Haeupler, Sen & Tarjan (2015) introduce the rank balanced trees framework for unifying the study of binary search tree by defining the rank binary tree, and each binary search tree follows by specific constraints applied to the rank function. Note that the framework doesn't specify the algorithms in which these trees are implemented.

A rank binary tree is a binary tree where each node x is associated with a rank r(x). By convention, empty node has rank -1. For a node x that is not the root, the rank difference is $r(p(x))-r(x)$ , and such a node is called an i-child if the rank difference is i. A node is of type $i,j$ if the rank difference of its left child and right child is i and j (disregarding ordering).

With that, we can define additional rules, which correspond to different trees:

AVL rule, which corresponds to AVL tree: each node is of type 1,1 or 1,2.
2-3 rule, which corresponds to the binarized 2-3 tree: each node is of type 0,1 or 1,1, and no parent of a 0-child is a 0-child.
Red black rule, which corresponds to Red-black tree: all rank differences are 0 or 1, and no parent of a 0-child is a 0-child. Note that the red-black rule generalizes the 2-3 rule by allowing for 0,0 type node.

So far all these rules are symmetric for the left node and the right node. By breaking such symmetries, it gives rise to other rules:

Right-Leaning Two-Three Rule, which corresponds to the right leaning binarized 2-3 tree: Every node is 1,1 or 0,1, no parent of a 0-child is a 0-child, and no 0-child is left.
Left-Leaning Two-Three Rule, which corresponds to the left leaning binarized 2-3 tree: Every node is 1,1 or 0,1, no parent of a 0-child is a 0-child, and no 0-child is right.
Right-leaning red-black rule, which corresponds to Reft-leaning red–black tree: no parent of a 0-child is a 0-child, and no 0-child of a 0,1-node is left.
Left-leaning red-black rule, which corresponds to Left-leaning red–black tree: all rank differences are 0 or 1, no parent of a 0-child is a 0-child, and no 0-child of a 0,1-node is right.

The weak AVL tree is defined by the weak AVL rule:

Weak AVL rule: all rank differences are 1 or 2, and all leaf nodes have rank 0.

Note that weak AVL tree generalizes the AVL tree by allowing for 2,2 type node. A simple proof shows that a weak AVL tree can be colored in a way that represents a red-black tree. So in a sense, weak AVL tree combines the properties of AVL tree and red-black tree.

Definition

As with binary search trees more generally, a WAVL tree consists of a collection of nodes, of two types: internal nodes and external nodes. An internal node stores a data item, and is linked to its parent (except for a designated root node that has no parent) and to exactly two children in the tree, the left child and the right child. An external node carries no data, and has a link only to its parent in the tree. These nodes are arranged to form a binary tree, so that for any internal node $x$ the parents of the left and right children of $x$ are $x$ itself. The external nodes form the leaves of the tree.[3] The data items are arranged in the tree in such a way that an inorder traversal of the tree lists the data items in sorted order.[4]

What distinguishes WAVL trees from other types of binary search tree is its use of ranks. These are numbers, associated with each node, that provide an approximation to the distance from the node to its farthest leaf descendant. Unlike in AVL trees, where ranks are defined to be the same as nodes' heights, ranks do not always equal to heights in WAVL trees. The rank difference of node x is defined as the difference between the rank of x's parent and the rank of x. The ranks are required to obey the following properties:[1][2]

External-Node Property: Every external node has rank $0$ [5]
Rank-Difference Property: If a non-root node has rank $r$ , then the rank of its parent must be either $r + 1$ or $r + 2$ . In other words, the rank difference for any non-root node is 1 or 2.[1]
Internal-Node Property: An internal node with two external children must have rank exactly 1.

Operations

Searching

Searching for a key $k$ in a WAVL tree is much the same as in any balanced binary search tree data structure. One begins at the root of the tree, and then repeatedly compares $k$ with the data item stored at each node on a path from the root, following the path to the left child of a node when $k$ is smaller than the value at the node or instead following the path to the right child when $k$ is larger than the value at the node. When a node with value equal to $k$ is reached, or an external node is reached, the search stops.[6]

If the search stops at an internal node, the key $k$ has been found. If instead, the search stops at an external node, then the position where $k$ would be inserted (if it were inserted) has been found.[6]

Insertion

Inserting an internal node with key $k$ into a WAVL tree requires a search for $k$ in the tree, ending at an external node, then a replacement of that external node with the new internal node with two external children, and finally a rebalancing of the tree. The rebalancing step can be performed either top-down or bottom-up,[2] but the bottom-up version of rebalancing is the one that most closely matches AVL trees.[1][2]

Bottom-up rebalancing begins by considering the rank-difference between a node - initially the newly inserted node - and its parent. If there is no parent, balance is restored. Before insertion began, the rank-difference between parent and node was 1 or 2, but that difference has been reduced by 1 because the subtree rooted at node has grown taller. If the new rank-difference between parent and node is 1, balance is restored. Otherwise, if the sibling, the other child of parent, has a rank-difference of 1 with the parent, promote the parent - increase its rank by increasing the rank-differences between it and each of its children - and continue rebalancing with the old parent as the new node.

Finally, with rank-differences of 0 and 2 for node and sibling, one or two tree rotations, with associated adjustments to rank-differences, can restore balance. The in-between child of node is the one with key between the keys of node and parent. If the rank-difference for that child and node is 2, rotate to move node up in the tree and parent down, then demote parent - reduce its rank by adjusting the rank-differences around it - and balance is restored. Otherwise, rotate to move the child up and the node down, then rotate again to move the child up and the parent down. Promote the child, demote the node and parent, and balance is restored.

Thus, overall, the insertion procedure consists of a search, the creation of a constant number of new nodes, a logarithmic number of rank changes, and a constant number of tree rotations.[1][2]

Deletion

Deleting an internal node from a WAVL tree starts with ordinary binary search tree deletion. For an internal node with no external child, that means finding its successor in the tree, exchanging the node with its successor, and then removing the node from its new tree position, where its left child is necessarily an external node. To remove an internal node with an external child, replace the node with the other child.

Bottom-up rebalancing begins by considering the rank-difference between a node - initially, the node that replaced the deleted node - and its parent. If there is no parent, balance is restored. Before deletion began, the rank-difference between parent and node was 1 or 2, but that difference has been increased by 1 because the subtree rooted at node has shortened. If the parent now has two external children, the internal-node property is violated because the parent has rank 2. The parent must be demoted, and rebalancing continued with the parent as the node that is the root of the too-short subtree.

If the node has no parent, balance is restored. If the rank-difference between node and parent has grown from 1 to 2, balance is restored. Otherwise, if the sibling, the other child of parent, has a rank-difference of 2 with the parent, demote the parent - decrease its rank by decreasing the rank-differences between it and each of its children - and continue rebalancing with the old parent as the new node. Otherwise, if the two children of the sibling have rank-differences of 2 with the sibling, demote the parent and the sibling and continue rebalancing with the old parent as the new node.

Finally, with rank-differences of 3 and 1 for node and sibling, and with sibling having a child with rank-difference 1, one or two tree rotations, with associated adjustments to rank-differences, can restore balance. Identify the children of the sibling as the niece and the nephew, where the key of the niece lies between the keys of the parent and sibling, and the key of the nephew does not. If the rank-difference between sibling and nephew is 1, rotate to move sibling up and parent down, promote the sibling, and demote the parent once, at least, and twice, if necessary to avoid violating the internal-node property. Otherwise, with the rank-difference between sibling and nephew as 1, rotate to move the niece up and the sibling down, rotate again to move the niece up and the parent down, promote the niece twice, demote the sibling once, and demote the parent twice.

Overall, a deletion consists of a search downward to find a node with an external child, the removal of a constant number of new nodes, a logarithmic number of rank changes, and a constant number of tree rotations.[1][2]

It is worthwhile to compare the result of a delete which would cause rotations at multiple levels in an AVL tree with the rotation and rank changes performed in a WAVL tree. In the second image the node with value 12 has been deleted followed by a right rotation and assigning of all external nodes rank zero.

Fibonacci Tree With Ranks

Fibonacci Tree With Ranks After Delete

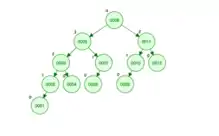
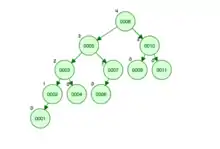
Computational complexity

Each search, insertion, or deletion in a WAVL tree involves following a single path in the tree and performing a constant number of steps for each node in the path. In a WAVL tree with $n$ items that has only undergone insertions, the maximum path length is $\log _{\varphi }n\approx 1.44\log _{2}n$ . If both insertions and deletions may have happened, the maximum path length is $2\log _{2}n$ . Therefore, in either case, the worst-case time for each search, insertion, or deletion in a WAVL tree with $n$ data items is $O (log n)$ .

Additionally, after finding a node for insertion and deletion, the amortized complexity of the tree restructuring operations is constant. Adding or deleting the node itself is constant time, the amount of rotations is always at most constant and it can be shown that the total amount of rank changes in the nodes is linear in the number of both insertions and deletions.

Related structures

WAVL trees are closely related to both AVL trees and red–black trees. Every AVL tree can have ranks assigned to its nodes in a way that makes it into a WAVL tree. And every WAVL tree can have its nodes colored red and black (and its ranks reassigned) in a way that makes it into a red–black tree. However, some WAVL trees do not come from AVL trees in this way and some red–black trees do not come from WAVL trees in this way.

AVL trees

An AVL tree is a kind of balanced binary search tree in which the two children of each internal node must have heights that differ by at most one.[7] The height of an external node is zero, and the height of any internal node is always one plus the maximum of the heights of its two children. Thus, the height function of an AVL tree obeys the constraints of a WAVL tree, and we may convert any AVL tree into a WAVL tree by using the height of each node as its rank.[1][2]

The key difference between an AVL tree and a WAVL tree arises when a node has two children with the same rank or height. In an AVL tree, if a node $x$ has two children of the same height $h$ as each other, then the height of $x$ must be exactly $h + 1$ . In contrast, in a WAVL tree, if a node $x$ has two children of the same rank $r$ as each other, then the rank of $x$ can be either $r + 1$ or $r + 2$ . This is because rank is not strictly equal to height in WAVL tree. This greater flexibility in ranks also leads to a greater flexibility in structures: some WAVL trees cannot be made into AVL trees even by modifying their ranks, because they include nodes whose children's heights differ by more than one.[2] However, we can say that all AVL trees are WAVL trees. AVL trees are WAVL trees without the type of node that has both children of rank difference 2.[1]

If a WAVL tree is created only using insertion operations, then its structure will be the same as the structure of an AVL tree created by the same insertion sequence, and its ranks will be the same as the ranks of the corresponding AVL tree. It is only through deletion operations that a WAVL tree can become different from an AVL tree. In particular this implies that a WAVL tree created only through insertions has height at most $\log _{\varphi }n\approx 1.44\log _{2}n$ .[2]

Red–black trees

A red–black tree is a balanced binary search tree in which each node has a color (red or black), satisfying the following properties:

External nodes are black.
If an internal node is red, its two children are both black.
All paths from the root to an external node have equal numbers of black nodes.

Red–black trees can equivalently be defined in terms of a system of ranks, stored at the nodes, satisfying the following requirements (different than the requirements for ranks in WAVL trees):

The rank of an external node is always 0 and its parent's rank is always 1.
The rank of any non-root node equals either its parent's rank or its parent's rank minus 1.
No two consecutive edges on any root-leaf path have rank difference 0.

The equivalence between the color-based and rank-based definitions can be seen, in one direction, by coloring a node black if its parent has greater rank and red if its parent has equal rank. In the other direction, colors can be converted to ranks by making the rank of a black node equal to the number of black nodes on any path to an external node, and by making the rank of a red node equal to its parent.[8]

The ranks of the nodes in a WAVL tree can be converted to a system of ranks of nodes, obeying the requirements for red–black trees, by dividing each rank by two and rounding up to the nearest integer.[9] Because of this conversion, for every WAVL tree there exists a valid red–black tree with the same structure. Because red–black trees have maximum height $2\log _{2}n$ , the same is true for WAVL trees.[1][2] However, there exist red–black trees that cannot be given a valid WAVL tree rank function.[2]

Despite the fact that, in terms of their tree structures, WAVL trees are special cases of red–black trees, their update operations are different. The tree rotations used in WAVL tree update operations may make changes that would not be permitted in a red–black tree, because they would in effect cause the recoloring of large subtrees of the red–black tree rather than making color changes only on a single path in the tree.[2] This allows WAVL trees to perform fewer tree rotations per deletion, in the worst case, than red-black trees.[1][2]

References

Goodrich, Michael T.; Tamassia, Roberto (2015), "4.4 Weak AVL Trees", Algorithm Design and Applications, Wiley, pp. 130–138.
Haeupler, Bernhard; Sen, Siddhartha; Tarjan, Robert E. (2015), "Rank-balanced trees" (PDF), ACM Transactions on Algorithms, 11 (4): Art. 30, 26, doi:10.1145/2689412, MR 3361215.
Goodrich & Tamassia (2015), Section 2.3 Trees, pp. 68–83.
Goodrich & Tamassia (2015), Chapter 3 Binary Search Trees, pp. 89–114.
In this we follow Goodrich & Tamassia (2015). In the version described by Haeupler, Sen & Tarjan (2015), the external nodes have rank −1. This variation makes very little difference in the operations of WAVL trees, but it causes some minor changes to the formula for converting WAVL trees to red–black trees.
Goodrich & Tamassia (2015), Section 3.1.2 Searching in a Binary Search Tree, pp. 95–96.
Goodrich & Tamassia (2015), Section 4.2 AVL Trees, pp. 120–125.
Goodrich & Tamassia (2015), Section 4.3 Red–black Trees, pp. 126–129.
In Haeupler, Sen & Tarjan (2015) the conversion is done by rounding down, because the ranks of external nodes are −1 rather than 0. Goodrich & Tamassia (2015) give a formula that also rounds down, but because they use rank 0 for external nodes their formula incorrectly assigns red–black rank 0 to internal nodes with WAVL rank 1.

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.

[gt-1] Goodrich, Michael T.; Tamassia, Roberto (2015), "4.4 Weak AVL Trees", Algorithm Design and Applications, Wiley, pp. 130–138.

[hst15-2] Haeupler, Bernhard; Sen, Siddhartha; Tarjan, Robert E. (2015), "Rank-balanced trees" (PDF), ACM Transactions on Algorithms, 11 (4): Art. 30, 26, doi:10.1145/2689412, MR 3361215.

[3] Goodrich & Tamassia (2015), Section 2.3 Trees, pp. 68–83.

[4] Goodrich & Tamassia (2015), Chapter 3 Binary Search Trees, pp. 89–114.

[5] In this we follow Goodrich & Tamassia (2015). In the version described by Haeupler, Sen & Tarjan (2015), the external nodes have rank −1. This variation makes very little difference in the operations of WAVL trees, but it causes some minor changes to the formula for converting WAVL trees to red–black trees.

[gt-search-6] Goodrich & Tamassia (2015), Section 3.1.2 Searching in a Binary Search Tree, pp. 95–96.

[7] Goodrich & Tamassia (2015), Section 4.2 AVL Trees, pp. 120–125.

[8] Goodrich & Tamassia (2015), Section 4.3 Red–black Trees, pp. 126–129.

[9] In Haeupler, Sen & Tarjan (2015) the conversion is done by rounding down, because the ranks of external nodes are −1 rather than 0. Goodrich & Tamassia (2015) give a formula that also rounds down, but because they use rank 0 for external nodes their formula incorrectly assigns red–black rank 0 to internal nodes with WAVL rank 1.