Wind-wave dissipation

The process of wind-wave dissipation can be explained by applying energy spectrum theory in a similar manner as for the formation of wind-waves (generally assuming spectral dissipation is a function of wave spectrum).[1] However, although even some of recent innovative improvements for field observations (such as Banner & Babanin et al.[2][3] ) have contributed to solve the riddles of wave breaking behaviors, unfortunately there hasn't been a clear understanding for exact theories of the wind wave dissipation process still yet because of its non-linear behaviors. By past and present observations and derived theories, the physics of the ocean-wave dissipation can be categorized by its passing regions along to water depth. In deep water, wave dissipation occurs by the actions of friction or drag forces such as opposite-directed winds or viscous forces generated by turbulent flows—usually nonlinear forces. In shallow water, the behaviors of wave dissipations are mostly types of shore wave breaking (see Types of wave breaking). Some of simple general descriptions of wind-wave dissipation (defined by Luigi Cavaleri et al.[1] ) were proposed when we consider only ocean surface waves such as wind waves. By means of the simple, the interactions of waves with the vertical structure of the upper layers of the ocean are ignored for simplified theory in many proposed mechanisms.[1]

In general understanding, the physics of wave dissipation can be categorized by considering with its dissipation sources, such as 1) wave breaking 2) wave–turbulence interaction 3) wave–wave modulation respectively.[1] (descriptions below of this chapter also follow the reference [1] )

1) dissipation by "wave breaking"

Wind-wave breaking at coastal area is a major source of the wind-wave dissipation. The wind waves lose their energy to the shore or sometimes back to the ocean when those break at the shore. (see more explains -> “Ocean surface wave breaking”)

2) dissipation by "wave–turbulence interaction"

The turbulent wind flows and viscous eddies inside waves can both affect wave dissipation. In the very early understandings, the viscosity could barely affect the wind waves, so that the dissipation of the swells by viscosity was also barely considered.[4][5] However, recent weather forecasting models begin considering “wave-turbulence interaction” for the wave modeling.[6] It is still arguable how much the turbulent-induced dissipations contribute to change the whole wave profiles, but the ideas of wave-turbulence interaction for surface viscous layers and wave bottom boundary layers are recently accepted.

3) dissipation by "wave-wave modulation"

Wave–wave interactions can affect to the wave dissipation. In the early eras, the ideas that a short wave breaking can take energy from the long waves through the modulation were proposed by Phillips (1963),[7] and Longuett-Higgins (1969) [8] as well. These ideas had been debated (new results that the dissipations by interactions between wave modulations should be much weaker than the theory's of Phillips) by Hasselmann's works (1971),[9] but in the recent understanding, the dissipations of these cases are typically little stronger than the dissipation by “wave-turbulence interactions” when the reasonable modulation transfer functions implemented.[10] Most cases of the swell dissipations are due to this dissipation type.[1]

Simple schematic of spilling breaker

Simple schematic of pulnging breaker

Simple schematic of surging breaker

When wind waves approach to coast area from deep water, the waves change their heights and lengths. The wave height becomes higher and the wavelength becomes shorter as the wave velocity is slowed when ocean waves approach to the shore. If the water depth is sufficiently shallow, the wave crest become steeper and the trough gets broader and shallower; finally, the ocean waves break at the shore. The motions of wave breaking are different with along to the steepness of shores and waves, and can be categorized by below three types.[11][12]

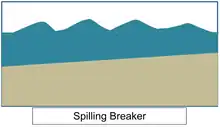
• Spilling breaker

With lower shore slope, the waves lose energy slowly as approaching to the shore. The waves spill sea water down the front of the waves when those are breaking.

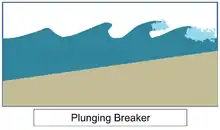
• Plunging breaker

With moderately steep shore slope, the wave loses energy quickly. If the shore slope is steep enough, the crest of wave moves faster than the trough. The crest curls over front of the wave, and after the crest plunges sea water to the trough. (Plunging breakers are good for surfing)

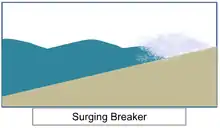
• Surging breaker

With highly steep shore slope (for extreme steepness, such as seawalls), if the shore steepness is very high, the waves can't reach to the critical steepness to break. The waves climb along through the shore slope, and release energy to the backward from the shore. It never shows white-cap breaks, but for extreme steepness case, such as seawall, the waves break with white-foams.

• Dispersion (water waves)

• Breaking and dissipation of ocean surface waves – Alexander V. Babanin