Fence (mathematics)
In mathematics, a fence, also called a zigzag poset, is a partially ordered set (poset) in which the order relations form a path with alternating orientations:
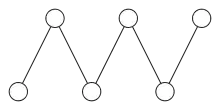
or
A fence may be finite, or it may be formed by an infinite alternating sequence extending in both directions. The incidence posets of path graphs form examples of fences.
A linear extension of a fence is called an alternating permutation; André's problem of counting the number of different linear extensions has been studied since the 19th century.[1] The solutions to this counting problem, the so-called Euler zigzag numbers or up/down numbers, are:
The number of antichains in a fence is a Fibonacci number; the distributive lattice with this many elements, generated from a fence via Birkhoff's representation theorem, has as its graph the Fibonacci cube.[2]
A partially ordered set is series-parallel if and only if it does not have four elements forming a fence.[3]
Several authors have also investigated the number of order-preserving maps from fences to themselves, or to fences of other sizes.[4]
An up-down poset Q(a,b) is a generalization of a zigzag poset in which there are a downward orientations for every upward one and b total elements.[5] For instance, Q(2,9) has the elements and relations
In this notation, a fence is a partially ordered set of the form Q(1,n).
Equivalent conditions
The following conditions are equivalent for a poset P:
- P is a disjoint union of zigzag posets.
- If a ≤ b ≤ c in P, either a = b or b = c.
- , i.e. it is never the case that a < b and b < c, so that < is vacuously transitive.
- P has dimension at most one (defined analogously to the Krull dimension of a commutative ring).
- Every element of P is either maximal or minimal.
- The slice category Pos/P is cartesian closed.[lower-alpha 1]
The prime ideals of a commutative ring R, ordered by inclusion, satisfy the equivalent conditions above if and only if R has Krull dimension at most one.
Notes
- Here, Pos denotes the category of partially ordered sets.
References
- André (1881).
- Gansner (1982) calls the fact that this lattice has a Fibonacci number of elements a “well known fact,” while Stanley (1986) asks for a description of it in an exercise. See also Höft & Höft (1985), Beck (1990), and Salvi & Salvi (2008).
- Valdes, Tarjan & Lawler (1982).
- Currie & Visentin (1991); Duffus et al. (1992); Rutkowski (1992a); Rutkowski (1992b); Farley (1995).
- Gansner (1982).
- André, Désiré (1881), "Sur les permutations alternées", J. Math. Pures Appl., (Ser. 3), 7: 167–184.
- Beck, István (1990), "Partial orders and the Fibonacci numbers", Fibonacci Quarterly, 28 (2): 172–174, MR 1051291.
- Currie, J. D.; Visentin, T. I. (1991), "The number of order-preserving maps of fences and crowns", Order, 8 (2): 133–142, doi:10.1007/BF00383399, hdl:10680/1724, MR 1137906, S2CID 122356472.
- Duffus, Dwight; Rödl, Vojtěch; Sands, Bill; Woodrow, Robert (1992), "Enumeration of order preserving maps", Order, 9 (1): 15–29, doi:10.1007/BF00419036, MR 1194849, S2CID 84180809.
- Farley, Jonathan David (1995), "The number of order-preserving maps between fences and crowns", Order, 12 (1): 5–44, doi:10.1007/BF01108588, MR 1336535, S2CID 120372679.
- Gansner, Emden R. (1982), "On the lattice of order ideals of an up-down poset", Discrete Mathematics, 39 (2): 113–122, doi:10.1016/0012-365X(82)90134-0, MR 0675856.
- Höft, Hartmut; Höft, Margret (1985), "A Fibonacci sequence of distributive lattices", Fibonacci Quarterly, 23 (3): 232–237, MR 0806293.
- Kelly, David; Rival, Ivan (1974), "Crowns, fences, and dismantlable lattices", Canadian Journal of Mathematics, 26 (5): 1257–1271, doi:10.4153/cjm-1974-120-2, MR 0417003.
- Rutkowski, Aleksander (1992a), "The number of strictly increasing mappings of fences", Order, 9 (1): 31–42, doi:10.1007/BF00419037, MR 1194850, S2CID 120965362.
- Rutkowski, Aleksander (1992b), "The formula for the number of order-preserving self-mappings of a fence", Order, 9 (2): 127–137, doi:10.1007/BF00814405, MR 1199291, S2CID 121879635.
- Salvi, Rodolfo; Salvi, Norma Zagaglia (2008), "Alternating unimodal sequences of Whitney numbers", Ars Combinatoria, 87: 105–117, MR 2414008.
- Stanley, Richard P. (1986), Enumerative Combinatorics, Wadsworth, Inc. Exercise 3.23a, page 157.
- Valdes, Jacobo; Tarjan, Robert E.; Lawler, Eugene L. (1982), "The Recognition of Series Parallel Digraphs", SIAM Journal on Computing, 11 (2): 298–313, doi:10.1137/0211023.