Multiple sequence alignment

Multiple sequence alignment (MSA) may refer to the process or the result of sequence alignment of three or more biological sequences, generally protein, DNA, or RNA. In many cases, the input set of query sequences are assumed to have an evolutionary relationship by which they share a linkage and are descended from a common ancestor. From the resulting MSA, sequence homology can be inferred and phylogenetic analysis can be conducted to assess the sequences' shared evolutionary origins. Visual depictions of the alignment as in the image at right illustrate mutation events such as point mutations (single amino acid or nucleotide changes) that appear as differing characters in a single alignment column, and insertion or deletion mutations (indels or gaps) that appear as hyphens in one or more of the sequences in the alignment. Multiple sequence alignment is often used to assess sequence conservation of protein domains, tertiary and secondary structures, and even individual amino acids or nucleotides.

First 90 positions of a protein multiple sequence alignment of instances of the acidic ribosomal protein P0 (L10E) from several organisms. Generated with ClustalX.

Computational algorithms are used to produce and analyse the MSAs due to the difficulty and intractability of manually processing the sequences given their biologically-relevant length. MSAs require more sophisticated methodologies than pairwise alignment because they are more computationally complex. Most multiple sequence alignment programs use heuristic methods rather than global optimization because identifying the optimal alignment between more than a few sequences of moderate length is prohibitively computationally expensive. On the other hand, heuristic methods generally fail to give guarantees on the solution quality, with heuristic solutions shown to be often far below the optimal solution on benchmark instances.[1][2][3]

Problem statement

Given sequences , similar to the form below:

A multiple sequence alignment is taken of this set of sequences by inserting any amount of gaps needed into each of the sequences of until the modified sequences, , all conform to length and no values in the sequences of of the same column consists of only gaps. The mathematical form of an MSA of the above sequence set is shown below:

To return from each particular sequence to , remove all gaps.

Graphing approach

A general approach when calculating multiple sequence alignments is to use graphs to identify all of the different alignments. When finding alignments via graph, a complete alignment is created in a weighted graph that contains a set of vertices and a set of edges. Each of the graph edges has a weight based on a certain heuristic that helps to score each alignment or subset of the original graph.

Tracing alignments

When determining the best suited alignments for each MSA, a trace is usually generated. A trace is a set of realized, or corresponding and aligned, vertices that has a specific weight based on the edges that are selected between corresponding vertices. When choosing traces for a set of sequences it is necessary to choose a trace with a maximum weight to get the best alignment of the sequences.

Alignment methods

There are various alignment methods used within multiple sequence to maximize scores and correctness of alignments. Each is usually based on a certain heuristic with an insight into the evolutionary process. Most try to replicate evolution to get the most realistic alignment possible to best predict relations between sequences.

Dynamic programming

A direct method for producing an MSA uses the dynamic programming technique to identify the globally optimal alignment solution. For proteins, this method usually involves two sets of parameters: a gap penalty and a substitution matrix assigning scores or probabilities to the alignment of each possible pair of amino acids based on the similarity of the amino acids' chemical properties and the evolutionary probability of the mutation. For nucleotide sequences, a similar gap penalty is used, but a much simpler substitution matrix, wherein only identical matches and mismatches are considered, is typical. The scores in the substitution matrix may be either all positive or a mix of positive and negative in the case of a global alignment, but must be both positive and negative, in the case of a local alignment.[4]

For n individual sequences, the naive method requires constructing the n-dimensional equivalent of the matrix formed in standard pairwise sequence alignment. The search space thus increases exponentially with increasing n and is also strongly dependent on sequence length. Expressed with the big O notation commonly used to measure computational complexity, a naïve MSA takes O(LengthNseqs) time to produce. To find the global optimum for n sequences this way has been shown to be an NP-complete problem.[5][6][7] In 1989, based on Carrillo-Lipman Algorithm,[8] Altschul introduced a practical method that uses pairwise alignments to constrain the n-dimensional search space.[9] In this approach pairwise dynamic programming alignments are performed on each pair of sequences in the query set, and only the space near the n-dimensional intersection of these alignments is searched for the n-way alignment. The MSA program optimizes the sum of all of the pairs of characters at each position in the alignment (the so-called sum of pair score) and has been implemented in a software program for constructing multiple sequence alignments.[10] In 2019, Hosseininasab and van Hoeve showed that by using decision diagrams, MSA may be modeled in polynomial space complexity.[3]

Progressive alignment construction

The most widely used approach to multiple sequence alignments uses a heuristic search known as progressive technique (also known as the hierarchical or tree method) developed by Da-Fei Feng and Doolittle in 1987.[11] Progressive alignment builds up a final MSA by combining pairwise alignments beginning with the most similar pair and progressing to the most distantly related. All progressive alignment methods require two stages: a first stage in which the relationships between the sequences are represented as a tree, called a guide tree, and a second step in which the MSA is built by adding the sequences sequentially to the growing MSA according to the guide tree. The initial guide tree is determined by an efficient clustering method such as neighbor-joining or UPGMA, and may use distances based on the number of identical two-letter sub-sequences (as in FASTA rather than a dynamic programming alignment).[12]

Progressive alignments are not guaranteed to be globally optimal. The primary problem is that when errors are made at any stage in growing the MSA, these errors are then propagated through to the final result. Performance is also particularly bad when all of the sequences in the set are rather distantly related. Most modern progressive methods modify their scoring function with a secondary weighting function that assigns scaling factors to individual members of the query set in a nonlinear fashion based on their phylogenetic distance from their nearest neighbors. This corrects for non-random selection of the sequences given to the alignment program.[12]

Progressive alignment methods are efficient enough to implement on a large scale for many (100s to 1000s) sequences. Progressive alignment services are commonly available on publicly accessible web servers so users need not locally install the applications of interest. The most popular progressive alignment method has been the Clustal family,[13] especially the weighted variant ClustalW[14] to which access is provided by a large number of web portals including GenomeNet, EBI, and EMBNet. Different portals or implementations can vary in user interface and make different parameters accessible to the user. ClustalW is used extensively for phylogenetic tree construction, in spite of the author's explicit warnings that unedited alignments should not be used in such studies and as input for protein structure prediction by homology modeling. Current version of Clustal family is ClustalW2. EMBL-EBI announced that CLustalW2 will be expired in August 2015. They recommend Clustal Omega which performs based on seeded guide trees and HMM profile-profile techniques for protein alignments. They offer different MSA tools for progressive DNA alignments. One of them is MAFFT (Multiple Alignment using Fast Fourier Transform).[15]

Another common progressive alignment method called T-Coffee[16] is slower than Clustal and its derivatives but generally produces more accurate alignments for distantly related sequence sets. T-Coffee calculates pairwise alignments by combining the direct alignment of the pair with indirect alignments that aligns each sequence of the pair to a third sequence. It uses the output from Clustal as well as another local alignment program LALIGN, which finds multiple regions of local alignment between two sequences. The resulting alignment and phylogenetic tree are used as a guide to produce new and more accurate weighting factors.

Because progressive methods are heuristics that are not guaranteed to converge to a global optimum, alignment quality can be difficult to evaluate and their true biological significance can be obscure. A semi-progressive method that improves alignment quality and does not use a lossy heuristic while still running in polynomial time has been implemented in the program PSAlign.[17]

Iterative methods

A set of methods to produce MSAs while reducing the errors inherent in progressive methods are classified as "iterative" because they work similarly to progressive methods but repeatedly realign the initial sequences as well as adding new sequences to the growing MSA. One reason progressive methods are so strongly dependent on a high-quality initial alignment is the fact that these alignments are always incorporated into the final result — that is, once a sequence has been aligned into the MSA, its alignment is not considered further. This approximation improves efficiency at the cost of accuracy. By contrast, iterative methods can return to previously calculated pairwise alignments or sub-MSAs incorporating subsets of the query sequence as a means of optimizing a general objective function such as finding a high-quality alignment score.[12]

A variety of subtly different iteration methods have been implemented and made available in software packages; reviews and comparisons have been useful but generally refrain from choosing a "best" technique.[18] The software package PRRN/PRRP uses a hill-climbing algorithm to optimize its MSA alignment score[19] and iteratively corrects both alignment weights and locally divergent or "gappy" regions of the growing MSA.[12] PRRP performs best when refining an alignment previously constructed by a faster method.[12]

Another iterative program, DIALIGN, takes an unusual approach of focusing narrowly on local alignments between sub-segments or sequence motifs without introducing a gap penalty.[20] The alignment of individual motifs is then achieved with a matrix representation similar to a dot-matrix plot in a pairwise alignment. An alternative method that uses fast local alignments as anchor points or "seeds" for a slower global-alignment procedure is implemented in the CHAOS/DIALIGN suite.[20]

A third popular iteration-based method called MUSCLE (multiple sequence alignment by log-expectation) improves on progressive methods with a more accurate distance measure to assess the relatedness of two sequences.[21] The distance measure is updated between iteration stages (although, in its original form, MUSCLE contained only 2-3 iterations depending on whether refinement was enabled).

Consensus methods

Consensus methods attempt to find the optimal multiple sequence alignment given multiple different alignments of the same set of sequences. There are two commonly used consensus methods, M-COFFEE and MergeAlign.[22] M-COFFEE uses multiple sequence alignments generated by seven different methods to generate consensus alignments. MergeAlign is capable of generating consensus alignments from any number of input alignments generated using different models of sequence evolution or different methods of multiple sequence alignment. The default option for MergeAlign is to infer a consensus alignment using alignments generated using 91 different models of protein sequence evolution.

Hidden Markov models
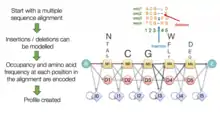
A profile HMM modelling a multiple sequence alignment

Hidden Markov models are probabilistic models that can assign likelihoods to all possible combinations of gaps, matches, and mismatches to determine the most likely MSA or set of possible MSAs. HMMs can produce a single highest-scoring output but can also generate a family of possible alignments that can then be evaluated for biological significance. HMMs can produce both global and local alignments. Although HMM-based methods have been developed relatively recently, they offer significant improvements in computational speed, especially for sequences that contain overlapping regions.[12]

Typical HMM-based methods work by representing an MSA as a form of directed acyclic graph known as a partial-order graph, which consists of a series of nodes representing possible entries in the columns of an MSA. In this representation a column that is absolutely conserved (that is, that all the sequences in the MSA share a particular character at a particular position) is coded as a single node with as many outgoing connections as there are possible characters in the next column of the alignment. In the terms of a typical hidden Markov model, the observed states are the individual alignment columns and the "hidden" states represent the presumed ancestral sequence from which the sequences in the query set are hypothesized to have descended. An efficient search variant of the dynamic programming method, known as the Viterbi algorithm, is generally used to successively align the growing MSA to the next sequence in the query set to produce a new MSA.[23] This is distinct from progressive alignment methods because the alignment of prior sequences is updated at each new sequence addition. However, like progressive methods, this technique can be influenced by the order in which the sequences in the query set are integrated into the alignment, especially when the sequences are distantly related.[12]

Several software programs are available in which variants of HMM-based methods have been implemented and which are noted for their scalability and efficiency, although properly using an HMM method is more complex than using more common progressive methods. The simplest is POA (Partial-Order Alignment);[24] a similar but more generalized method is implemented in the packages SAM (Sequence Alignment and Modeling System).[25] and HMMER.[26] SAM has been used as a source of alignments for protein structure prediction to participate in the CASP structure prediction experiment and to develop a database of predicted proteins in the yeast species S. cerevisiae. HHsearch[27] is a software package for the detection of remotely related protein sequences based on the pairwise comparison of HMMs. A server running HHsearch (HHpred) was by far the fastest of the 10 best automatic structure prediction servers in the CASP7 and CASP8 structure prediction competitions.[28]

Phylogeny-aware methods
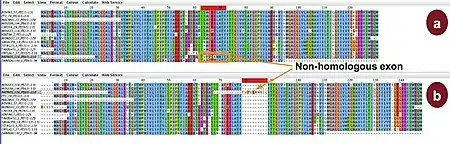
Non-homologous exon alignment by an iterative method (a), and by a phylogeny-aware method (b)

Most multiple sequence alignment methods try to minimize the number of insertions/deletions (gaps) and, as a consequence, produce compact alignments. This causes several problems if the sequences to be aligned contain non-homologous regions, if gaps are informative in a phylogeny analysis. These problems are common in newly produced sequences that are poorly annotated and may contain frame-shifts, wrong domains or non-homologous spliced exons. The first such method was developed in 2005 by Löytynoja and Goldman.[29] The same authors released a software package called PRANK in 2008.[30] PRANK improves alignments when insertions are present. Nevertheless, it runs slowly compared to progressive and/or iterative methods which have been developed for several years.

In 2012, two new phylogeny-aware tools appeared. One is called PAGAN that was developed by the same team as PRANK.[31] The other is ProGraphMSA developed by Szalkowski.[32] Both software packages were developed independently but share common features, notably the use of graph algorithms to improve the recognition of non-homologous regions, and an improvement in code making these software faster than PRANK.

Motif finding
Alignment of the seven Drosophila caspases colored by motifs as identified by MEME. When motif positions and sequence alignments are generated independently, they often correlate well but not perfectly, as in this example.

Motif finding, also known as profile analysis, is a method of locating sequence motifs in global MSAs that is both a means of producing a better MSA and a means of producing a scoring matrix for use in searching other sequences for similar motifs. A variety of methods for isolating the motifs have been developed, but all are based on identifying short highly conserved patterns within the larger alignment and constructing a matrix similar to a substitution matrix that reflects the amino acid or nucleotide composition of each position in the putative motif. The alignment can then be refined using these matrices. In standard profile analysis, the matrix includes entries for each possible character as well as entries for gaps.[12] Alternatively, statistical pattern-finding algorithms can identify motifs as a precursor to an MSA rather than as a derivation. In many cases when the query set contains only a small number of sequences or contains only highly related sequences, pseudocounts are added to normalize the distribution reflected in the scoring matrix. In particular, this corrects zero-probability entries in the matrix to values that are small but nonzero.

Blocks analysis is a method of motif finding that restricts motifs to ungapped regions in the alignment. Blocks can be generated from an MSA or they can be extracted from unaligned sequences using a precalculated set of common motifs previously generated from known gene families.[33] Block scoring generally relies on the spacing of high-frequency characters rather than on the calculation of an explicit substitution matrix. The BLOCKS server provides an interactive method to locate such motifs in unaligned sequences.

Statistical pattern-matching has been implemented using both the expectation-maximization algorithm and the Gibbs sampler. One of the most common motif-finding tools, known as MEME, uses expectation maximization and hidden Markov methods to generate motifs that are then used as search tools by its companion MAST in the combined suite MEME/MAST Archived 2010-08-22 at the Wayback Machine.[34][35]

Non-coding multiple sequence alignment

Non-coding DNA regions, especially TFBSs, are rather more conserved and not necessarily evolutionarily related, and may have converged from non-common ancestors. Thus, the assumptions used to align protein sequences and DNA coding regions are inherently different from those that hold for TFBS sequences. Although it is meaningful to align DNA coding regions for homologous sequences using mutation operators, alignment of binding site sequences for the same transcription factor cannot rely on evolutionary related mutation operations. Similarly, the evolutionary operator of point mutations can be used to define an edit distance for coding sequences, but this has little meaning for TFBS sequences because any sequence variation has to maintain a certain level of specificity for the binding site to function. This becomes specifically important when trying to align known TFBS sequences to build supervised models to predict unknown locations of the same TFBS. Hence, Multiple Sequence Alignment methods need to adjust the underlying evolutionary hypothesis and the operators used as in the work published incorporating neighbouring base thermodynamic information [36] to align the binding sites searching for the lowest thermodynamic alignment conserving specificity of the binding site, EDNA .

Optimization

Genetic algorithms and simulated annealing

Standard optimization techniques in computer science — both of which were inspired by, but do not directly reproduce, physical processes — have also been used in an attempt to more efficiently produce quality MSAs. One such technique, genetic algorithms, has been used for MSA production in an attempt to broadly simulate the hypothesized evolutionary process that gave rise to the divergence in the query set. The method works by breaking a series of possible MSAs into fragments and repeatedly rearranging those fragments with the introduction of gaps at varying positions. A general objective function is optimized during the simulation, most generally the "sum of pairs" maximization function introduced in dynamic programming-based MSA methods. A technique for protein sequences has been implemented in the software program SAGA (Sequence Alignment by Genetic Algorithm)[37] and its equivalent in RNA is called RAGA.[38]

The technique of simulated annealing, by which an existing MSA produced by another method is refined by a series of rearrangements designed to find better regions of alignment space than the one the input alignment already occupies. Like the genetic algorithm method, simulated annealing maximizes an objective function like the sum-of-pairs function. Simulated annealing uses a metaphorical "temperature factor" that determines the rate at which rearrangements proceed and the likelihood of each rearrangement; typical usage alternates periods of high rearrangement rates with relatively low likelihood (to explore more distant regions of alignment space) with periods of lower rates and higher likelihoods to more thoroughly explore local minima near the newly "colonized" regions. This approach has been implemented in the program MSASA (Multiple Sequence Alignment by Simulated Annealing).[39]

Mathematical programming and exact solution algorithms

Mathematical programming and in particular Mixed integer programming models are another approach to solve MSA problems. The advantage of such optimization models is that they can be used to find the optimal MSA solution more efficiently compared to the traditional DP approach. This is due in part, to the applicability of decomposition techniques for mathematical programs, where the MSA model is decomposed into smaller parts and iteratively solved until the optimal solution is found. Example algorithms used to solve mixed integer programming models of MSA include branch and price[40] and Benders decomposition.[3] Although exact approaches are computationally slow compared to heuristic algorithms for MSA, they are guaranteed to reach the optimal solution eventually, even for large-size problems.

Simulated quantum computing

In January 2017, D-Wave Systems announced that its qbsolv open-source quantum computing software had been successfully used to find a faster solution to the MSA problem.[41]

Alignment visualization and quality control

The necessary use of heuristics for multiple alignment means that for an arbitrary set of proteins, there is always a good chance that an alignment will contain errors. For example, an evaluation of several leading alignment programs using the BAliBase benchmark found that at least 24% of all pairs of aligned amino acids were incorrectly aligned.[2] These errors can arise because of unique insertions into one or more regions of sequences, or through some more complex evolutionary process leading to proteins that do not align easily by sequence alone. As the number of sequence and their divergence increases many more errors will be made simply because of the heuristic nature of MSA algorithms. Multiple sequence alignment viewers enable alignments to be visually reviewed, often by inspecting the quality of alignment for annotated functional sites on two or more sequences. Many also enable the alignment to be edited to correct these (usually minor) errors, in order to obtain an optimal 'curated' alignment suitable for use in phylogenetic analysis or comparative modeling.[42]

However, as the number of sequences increases and especially in genome-wide studies that involve many MSAs it is impossible to manually curate all alignments. Furthermore, manual curation is subjective. And finally, even the best expert cannot confidently align the more ambiguous cases of highly diverged sequences. In such cases it is common practice to use automatic procedures to exclude unreliably aligned regions from the MSA. For the purpose of phylogeny reconstruction (see below) the Gblocks program is widely used to remove alignment blocks suspect of low quality, according to various cutoffs on the number of gapped sequences in alignment columns.[43] However, these criteria may excessively filter out regions with insertion/deletion events that may still be aligned reliably, and these regions might be desirable for other purposes such as detection of positive selection. A few alignment algorithms output site-specific scores that allow the selection of high-confidence regions. Such a service was first offered by the SOAP program,[44] which tests the robustness of each column to perturbation in the parameters of the popular alignment program CLUSTALW. The T-Coffee program[45] uses a library of alignments in the construction of the final MSA, and its output MSA is colored according to confidence scores that reflect the agreement between different alignments in the library regarding each aligned residue. Its extension, TCS : (Transitive Consistency Score), uses T-Coffee libraries of pairwise alignments to evaluate any third party MSA. Pairwise projections can be produced using fast or slow methods, thus allowing a trade-off between speed and accuracy.[46][47] Another alignment program that can output an MSA with confidence scores is FSA,[48] which uses a statistical model that allows calculation of the uncertainty in the alignment. The HoT (Heads-Or-Tails) score can be used as a measure of site-specific alignment uncertainty due to the existence of multiple co-optimal solutions.[49] The GUIDANCE program[50] calculates a similar site-specific confidence measure based on the robustness of the alignment to uncertainty in the guide tree that is used in progressive alignment programs. An alternative, more statistically justified approach to assess alignment uncertainty is the use of probabilistic evolutionary models for joint estimation of phylogeny and alignment. A Bayesian approach allows calculation of posterior probabilities of estimated phylogeny and alignment, which is a measure of the confidence in these estimates. In this case, a posterior probability can be calculated for each site in the alignment. Such an approach was implemented in the program BAli-Phy.[51]

There are free programs available for visualization of multiple sequence alignments, for example Jalview and UGENE.

Phylogenetic use

Multiple sequence alignments can be used to create a phylogenetic tree.[52] This is made possible by two reasons. The first is because functional domains that are known in annotated sequences can be used for alignment in non-annotated sequences. The other is that conserved regions known to be functionally important can be found. This makes it possible for multiple sequence alignments to be used to analyze and find evolutionary relationships through homology between sequences. Point mutations and insertion or deletion events (called indels) can be detected.

Multiple sequence alignments can also be used to identify functionally important sites, such as binding sites, active sites, or sites corresponding to other key functions, by locating conserved domains. When looking at multiple sequence alignments, it is useful to consider different aspects of the sequences when comparing sequences. These aspects include identity, similarity, and homology. Identity means that the sequences have identical residues at their respective positions. On the other hand, similarity has to do with the sequences being compared having similar residues quantitatively. For example, in terms of nucleotide sequences, pyrimidines are considered similar to each other, as are purines. Similarity ultimately leads to homology, in that the more similar sequences are, the closer they are to being homologous. This similarity in sequences can then go on to help find common ancestry.[52]

See also
  • Alignment-free sequence analysis
  • Cladistics
  • Generalized tree alignment
  • Multiple sequence alignment viewers
  • PANDIT, a biological database covering protein domains
  • Phylogenetics
    • Phylo
  • Sequence alignment software
  • Structural alignment

References
  1. Thompson JD, Linard B, Lecompte O, Poch O (2011). "A comprehensive benchmark study of multiple sequence alignment methods: current challenges and future perspectives". PLOS ONE. 6 (3): e18093. Bibcode:2011PLoSO...618093T. doi:10.1371/journal.pone.0018093. PMC 3069049. PMID 21483869.
  2. Nuin PA, Wang Z, Tillier ER (2006). "The accuracy of several multiple sequence alignment programs for proteins". BMC Bioinformatics. 7: 471. doi:10.1186/1471-2105-7-471. PMC 1633746. PMID 17062146.
  3. Hosseininasab A, van Hoeve WJ (2019). "Exact Multiple Sequence Alignment by Synchronized Decision Diagrams". INFORMS Journal on Computing. doi:10.1287/ijoc.2019.0937. S2CID 109937203.
  4. "Help with matrices used in sequence comparison tools". European Bioinformatics Institute. Archived from the original on March 11, 2010. Retrieved March 3, 2010.
  5. Wang L, Jiang T (1994). "On the complexity of multiple sequence alignment". J Comput Biol. 1 (4): 337–348. CiteSeerX 10.1.1.408.894. doi:10.1089/cmb.1994.1.337. PMID 8790475.
  6. Just W (2001). "Computational complexity of multiple sequence alignment with SP-score". J Comput Biol. 8 (6): 615–23. CiteSeerX 10.1.1.31.6382. doi:10.1089/106652701753307511. PMID 11747615.
  7. Elias, Isaac (2006). "Settling the intractability of multiple alignment". J Comput Biol. 13 (7): 1323–1339. CiteSeerX 10.1.1.6.256. doi:10.1089/cmb.2006.13.1323. PMID 17037961.
  8. Carrillo H, Lipman DJ (1988). "The Multiple Sequence Alignment Problem in Biology". SIAM Journal on Applied Mathematics. 48 (5): 1073–1082. doi:10.1137/0148063.
  9. Lipman DJ, Altschul SF, Kececioglu JD (1989). "A tool for multiple sequence alignment". Proc Natl Acad Sci U S A. 86 (12): 4412–4415. Bibcode:1989PNAS...86.4412L. doi:10.1073/pnas.86.12.4412. PMC 287279. PMID 2734293.
  10. "Genetic analysis software". National Center for Biotechnology Information. Retrieved March 3, 2010.
  11. Feng DF, Doolittle RF (1987). "Progressive sequence alignment as a prerequisitetto correct phylogenetic trees". J Mol Evol. 25 (4): 351–360. Bibcode:1987JMolE..25..351F. doi:10.1007/BF02603120. PMID 3118049. S2CID 6345432.
  12. Mount DM. (2004). Bioinformatics: Sequence and Genome Analysis 2nd ed. Cold Spring Harbor Laboratory Press: Cold Spring Harbor, NY.
  13. Higgins DG, Sharp PM (1988). "CLUSTAL: a package for performing multiple sequence alignment on a microcomputer". Gene. 73 (1): 237–244. doi:10.1016/0378-1119(88)90330-7. PMID 3243435.
  14. Thompson JD, Higgins DG, Gibson TJ (November 1994). "CLUSTAL W: improving the sensitivity of progressive multiple sequence alignment through sequence weighting, position-specific gap penalties and weight matrix choice". Nucleic Acids Res. 22 (22): 4673–80. doi:10.1093/nar/22.22.4673. PMC 308517. PMID 7984417.
  15. "EMBL-EBI-ClustalW2-Multiple Sequence Alignment". CLUSTALW2.
  16. Notredame C, Higgins DG, Heringa J (September 2000). "T-Coffee: A novel method for fast and accurate multiple sequence alignment". J. Mol. Biol. 302 (1): 205–17. doi:10.1006/jmbi.2000.4042. PMID 10964570. S2CID 10189971.
  17. Sze SH, Lu Y, Yang Q (2006). "A polynomial time solvable formulation of multiple sequence alignment". J Comput Biol. 13 (2): 309–319. doi:10.1089/cmb.2006.13.309. PMID 16597242.
  18. Hirosawa M, Totoki Y, Hoshida M, Ishikawa M (1995). "Comprehensive study on iterative algorithms of multiple sequence alignment". Comput Appl Biosci. 11 (1): 13–18. doi:10.1093/bioinformatics/11.1.13. PMID 7796270.
  19. Gotoh O (1996). "Significant improvement in accuracy of multiple protein sequence alignments by iterative refinement as assessed by reference to structural alignments". J Mol Biol. 264 (4): 823–38. doi:10.1006/jmbi.1996.0679. PMID 8980688.
  20. Brudno M, Chapman M, Göttgens B, Batzoglou S, Morgenstern B (December 2003). "Fast and sensitive multiple alignment of large genomic sequences". BMC Bioinformatics. 4: 66. doi:10.1186/1471-2105-4-66. PMC 521198. PMID 14693042.
  21. Edgar RC (2004). "MUSCLE: multiple sequence alignment with high accuracy and high throughput". Nucleic Acids Research. 32 (5): 1792–97. doi:10.1093/nar/gkh340. PMC 390337. PMID 15034147.
  22. Collingridge PW, Kelly S (2012). "MergeAlign: improving multiple sequence alignment performance by dynamic reconstruction of consensus multiple sequence alignments". BMC Bioinformatics. 13 (117): 117. doi:10.1186/1471-2105-13-117. PMC 3413523. PMID 22646090.
  23. Hughey R, Krogh A (1996). "Hidden Markov models for sequence analysis: extension and analysis of the basic method". CABIOS. 12 (2): 95–107. CiteSeerX 10.1.1.44.3365. doi:10.1093/bioinformatics/12.2.95. PMID 8744772.
  24. Grasso C, Lee C (2004). "Combining partial order alignment and progressive multiple sequence alignment increases alignment speed and scalability to very large alignment problems". Bioinformatics. 20 (10): 1546–56. doi:10.1093/bioinformatics/bth126. PMID 14962922.
  25. Hughey R, Krogh A. SAM: Sequence alignment and modeling software system. Technical Report UCSC-CRL-96-22, University of California, Santa Cruz, CA, September 1996.
  26. Durbin R, Eddy S, Krogh A, Mitchison G. (1998). Biological sequence analysis: probabilistic models of proteins and nucleic acids, Cambridge University Press, 1998.
  27. Söding J (2005). "Protein homology detection by HMM-HMM comparison". Bioinformatics. 21 (7): 951–960. CiteSeerX 10.1.1.519.1257. doi:10.1093/bioinformatics/bti125. PMID 15531603.
  28. Battey JN, Kopp J, Bordoli L, Read RJ, Clarke ND, Schwede T (2007). "Automated server predictions in CASP7". Proteins. 69 (Suppl 8): 68–82. doi:10.1002/prot.21761. PMID 17894354. S2CID 29879391.
  29. Loytynoja, A. (2005). "An algorithm for progressive multiple alignment of sequences with insertions". Proceedings of the National Academy of Sciences. 102 (30): 10557–10562. Bibcode:2005PNAS..10210557L. doi:10.1073/pnas.0409137102. PMC 1180752. PMID 16000407.
  30. Löytynoja A, Goldman N (June 2008). "Phylogeny-aware gap placement prevents errors in sequence alignment and evolutionary analysis". Science. 320 (5883): 1632–5. Bibcode:2008Sci...320.1632L. doi:10.1126/science.1158395. PMID 18566285. S2CID 5211928.
  31. Löytynoja A, Vilella AJ, Goldman N (July 2012). "Accurate extension of multiple sequence alignments using a phylogeny-aware graph algorithm". Bioinformatics. 28 (13): 1684–91. doi:10.1093/bioinformatics/bts198. PMC 3381962. PMID 22531217.
  32. Szalkowski AM (June 2012). "Fast and robust multiple sequence alignment with phylogeny-aware gap placement". BMC Bioinformatics. 13: 129. doi:10.1186/1471-2105-13-129. PMC 3495709. PMID 22694311.
  33. Henikoff S, Henikoff JG (December 1991). "Automated assembly of protein blocks for database searching". Nucleic Acids Res. 19 (23): 6565–72. doi:10.1093/nar/19.23.6565. PMC 329220. PMID 1754394.
  34. Bailey TL, Elkan C (1994). "Fitting a mixture model by expectation maximization to discover motifs in biopolymers" (PDF). Proceedings of the Second International Conference on Intelligent Systems for Molecular Biology. Menlo Park, California: AAAI Press. pp. 28–36.
  35. Bailey TL, Gribskov M (1998). "Combining evidence using p-values: application to sequence homology searches". Bioinformatics. 14 (1): 48–54. doi:10.1093/bioinformatics/14.1.48. PMID 9520501.
  36. Salama RA, Stekel DJ (November 2013). "A non-independent energy-based multiple sequence alignment improves prediction of transcription factor binding sites". Bioinformatics. 29 (21): 2699–704. doi:10.1093/bioinformatics/btt463. PMID 23990411.
  37. Notredame C, Higgins DG (April 1996). "SAGA: sequence alignment by genetic algorithm". Nucleic Acids Res. 24 (8): 1515–24. doi:10.1093/nar/24.8.1515. PMC 145823. PMID 8628686.
  38. Notredame C, O'Brien EA, Higgins DG (1997). "RAGA: RNA sequence alignment by genetic algorithm". Nucleic Acids Res. 25 (22): 4570–80. doi:10.1093/nar/25.22.4570. PMC 147093. PMID 9358168.
  39. Kim J, Pramanik S, Chung MJ (1994). "Multiple sequence alignment using simulated annealing". Comput Appl Biosci. 10 (4): 419–26. doi:10.1093/bioinformatics/10.4.419. PMID 7804875.
  40. Althaus E, Caprara A, Lenhof HP, Reinert K (2006). "A branch-and-cut algorithm for multiple sequence alignment". Mathematical Programming. 105 (2–3): 387–425. doi:10.1007/s10107-005-0659-3. S2CID 17715172.
  41. D-Wave Initiates Open Quantum Software Environment 11 January 2017
  42. "Manual editing and adjustment of MSAs". European Molecular Biology Laboratory. 2007. Archived from the original on September 24, 2015. Retrieved March 7, 2010.
  43. Castresana J (April 2000). "Selection of conserved blocks from multiple alignments for their use in phylogenetic analysis". Mol. Biol. Evol. 17 (4): 540–52. doi:10.1093/oxfordjournals.molbev.a026334. PMID 10742046.
  44. Löytynoja A, Milinkovitch MC (June 2001). "SOAP, cleaning multiple alignments from unstable blocks". Bioinformatics. 17 (6): 573–4. doi:10.1093/bioinformatics/17.6.573. PMID 11395440.
  45. Poirot O, O'Toole E, Notredame C (July 2003). "Tcoffee@igs: A web server for computing, evaluating and combining multiple sequence alignments". Nucleic Acids Res. 31 (13): 3503–6. doi:10.1093/nar/gkg522. PMC 168929. PMID 12824354.
  46. Chang, JM; Di Tommaso, P; Notredame, C (Jun 2014). "TCS: A New Multiple Sequence Alignment Reliability Measure to Estimate Alignment Accuracy and Improve Phylogenetic Tree Reconstruction". Molecular Biology and Evolution. 31 (6): 1625–37. doi:10.1093/molbev/msu117. PMID 24694831.
  47. Chang JM, Di Tommaso P, Lefort V, Gascuel O, Notredame C (July 2015). "TCS: a web server for multiple sequence alignment evaluation and phylogenetic reconstruction". Nucleic Acids Res. 43 (W1): W3–6. doi:10.1093/nar/gkv310. PMC 4489230. PMID 25855806.
  48. Bradley RK, Roberts A, Smoot M, Juvekar S, Do J, Dewey C, Holmes I, Pachter L (May 2009). "Fast statistical alignment". PLOS Comput. Biol. 5 (5): e1000392. Bibcode:2009PLSCB...5E0392B. doi:10.1371/journal.pcbi.1000392. PMC 2684580. PMID 19478997.
  49. Landan G, Graur D (2008). "Local reliability measures from sets of co-optimal multiple sequence alignments". Biocomputing 2008. Pac Symp Biocomput. pp. 15–24. doi:10.1142/9789812776136_0003. ISBN 978-981-277-608-2. PMID 18229673.
  50. Penn O, Privman E, Landan G, Graur D, Pupko T (August 2010). "An alignment confidence score capturing robustness to guide tree uncertainty". Mol. Biol. Evol. 27 (8): 1759–67. doi:10.1093/molbev/msq066. PMC 2908709. PMID 20207713.
  51. Redelings BD, Suchard MA (June 2005). "Joint Bayesian estimation of alignment and phylogeny". Syst. Biol. 54 (3): 401–18. doi:10.1080/10635150590947041. PMID 16012107.
  52. Budd, Aidan (10 February 2009). "Multiple sequence alignment exercises and demonstrations". European Molecular Biology Laboratory. Archived from the original on 5 March 2012. Retrieved June 30, 2010.

Survey articles

Lecture notes, tutorials, and courses

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.