Covering space
A covering of a topological space is a continuous map with special properties.
Definition
Let be a topological space. A covering of is a continuous map
such that there exists a discrete space and for every an open neighborhood , such that and is a homeomorphism for every .

Often, the notion of a covering is used for the covering space as well as for the map . The open sets are called sheets, which are uniquely determined up to a homeomorphism if is connected.[1]: 56 For a the discrete subset is called the fiber of . The degree of a covering is the cardinality of the space . If is path-connected, then the covering is denoted as a path-connected covering.
Examples
- For every topological space there exists the covering with , which is denoted as the trivial covering of
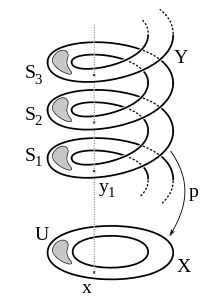
- The map with is a covering of the unit circle . The base of the covering is and the covering space is . For any point such that , the set is an open neighborhood of . The preimage of under is
- and the sheets of the covering are for The fiber of is
- Another covering of the unit circle is the map with for some For an open neighborhood of an , one has:
- .
- A map which is a local homeomorphism but not a covering of the unit circle is with . There is a sheet of an open neighborhood of , which is not mapped homeomorphically onto .
Properties
Local homeomorphism
Since a covering maps each of the disjoint open sets of homeomorphically onto it is a local homeomorphism, i.e. is a continuous map and for every there exists an open neighborhood of , such that is a homeomorphism.
It follows that the covering space and the base space locally share the same properties.
- If is a connected and non-orientable manifold, then there is a covering of degree , whereby is a connected and orientable manifold.[1]: 234
- If is a connected Lie group, then there is a covering which is also a Lie group homomorphism and is a Lie group.[2]: 174
- If is a graph, then it follows for a covering that is also a graph.[1]: 85
- If is a connected manifold, then there is a covering , whereby is a connected and simply connected manifold.[3]: 32
- If is a connected Riemann surface, then there is a covering which is also a holomorphic map[3]: 22 and is a connected and simply connected Riemann surface.[3]: 32
Factorisation
Let and be continuous maps, such that the diagram

commutes.
- If and are coverings, so is .
- If and are coverings, so is .[4]: 485
Product of coverings
Let and be topological spaces and and be coverings, then with is a covering.[4]: 339
Equivalence of coverings
Let be a topological space and and be coverings. Both coverings are called equivalent, if there exists a homeomorphism , such that the diagram

commutes. If such a homeomorphism exists, then one calls the covering spaces and isomorphic.
Lifting property
An important property of the covering is, that it satisfies the lifting property, i.e.:
Let be the unit interval and be a covering. Let be a continuous map and be a lift of , i.e. a continuous map such that . Then there is a uniquely determined, continuous map , which is a lift of , i.e. .[1]: 60
If is a path-connected space, then for it follows that the map is a lift of a path in and for it is a lift of a homotopy of paths in .
Because of that property one can show, that the fundamental group of the unit circle is an infinite cyclic group, which is generated by the homotopy classes of the loop with .[1]: 29
Let be a path-connected space and be a connected covering. Let be any two points, which are connected by a path , i.e. and . Let be the unique lift of , then the map
- with
If is a path-connected space and a connected covering, then the induced group homomorphism
- with ,
is injective and the subgroup of consists of the homotopy classes of loops in , whose lifts are loops in .[1]: 61
Branched covering
Holomorphic maps between Riemann surfaces
Let and be Riemann surfaces, i.e. one dimensional complex manifolds, and let be a continuous map. is holomorphic in a point , if for any charts of and of , with , the map is holomorphic.
If is holomorphic at all , we say is holomorphic.
The map is called the local expression of in .
If is a non-constant, holomorphic map between compact Riemann surfaces, then is surjective and an open map,[3]: 11 i.e. for every open set the image is also open.
Ramification point and branch point
Let be a non-constant, holomorphic map between compact Riemann surfaces. For every there exist charts for and and there exists a uniquely determined , such that the local expression of in is of the form .[3]: 10 The number is called the ramification index of in and the point is called a ramification point if . If for an , then is unramified. The image point of a ramification point is called a branch point.
Degree of a holomorphic map
Let be a non-constant, holomorphic map between compact Riemann surfaces. The degree of is the cardinality of the fiber of an unramified point , i.e. .
This number is well-defined, since for every the fiber is discrete[3]: 20 and for any two unramified points , it is:
It can be calculated by:
- [3]: 29
Definition
A continuous map is called a branched covering, if there exists a closed set with dense complement , such that is a covering.
Examples
- Let and , then with is branched covering of degree , whereby is a branch point.
- Every non-constant, holomorphic map between compact Riemann surfaces of degree is a branched covering of degree .
Universal covering
Definition
Let be a simply connected covering. If is another simply connected covering, then there exists a uniquely determined homeomorphism , such that the diagram
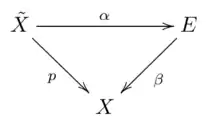
commutes.[4]: 482
This means that is, up to equivalence, uniquely determined and because of that universal property denoted as the universal covering of the space .
Existence
A universal covering does not always exist, but the following properties guarantee its existence:
Let be a connected, locally simply connected, then there exists a universal covering .
is defined as and by .[1]: 64
The topology on is constructed as follows: Let be a path with . Let be a simply connected neighborhood of the endpoint , then for every the paths inside from to are uniquely determined up to homotopy. Now consider , then with is a bijection and can be equipped with the final topology of .
The fundamental group acts freely through on and with is a homeomorphism, i.e. .
Examples
- with is the universal covering of the unit circle .
- with is the universal covering of the projective space for .
- with is the universal covering of the unitary group .[5]: 5, Theorem 1
- Since , it follows that the quotient map is the universal covering of the .
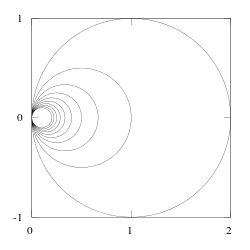 The Hawaiian earring. Only the ten largest circles are shown.
The Hawaiian earring. Only the ten largest circles are shown. - A topological space which has no universal covering is the Hawaiian earring:
- One can show that no neighborhood of the origin is simply connected.[4]: 487, Example 1
Deck transformation
Definition
Let be a covering. A deck transformation is a homeomorphism , such that the diagram of continuous maps

commutes. Together with the composition of maps, the set of deck transformation forms a group , which is the same as .
Examples
- Let be the covering for some , then the map is a deck transformation and .
- Let be the covering , then the map with is a deck transformation and .
Properties
Let be a path-connected space and be a connected covering. Since a deck transformation is bijective, it permutes the elements of a fiber with and is uniquely determined by where it sends a single point. In particular, only the identity map fixes a point in the fiber.[1]: 70 Because of this property every deck transformation defines a group action on , i.e. let be an open neighborhood of a and an open neighborhood of an , then is a group action.
Definition
A covering is called normal, if . This means, that for every and any two there exists a deck transformation , such that .
Properties
Let be a path-connected space and be a connected covering. Let be a subgroup of , then is a normal covering iff is a normal subgroup of .
If is a normal covering and , then .
If is a path-connected covering and , then , whereby is the normaliser of .[1]: 71
Let be a topological space. A group acts discontinuously on , if every has an open neighborhood with , such that for every with one has .
If a group acts discontinuously on a topological space , then the quotient map with is a normal covering.[1]: 72 Hereby is the quotient space and is the orbit of the group action.
Examples
- The covering with is a normal coverings for every .
- Every simply connected covering is a normal covering.
Calculation
Let be a group, which acts discontinuously on a topological space and let be the normal covering.
- If is path-connected, then .[1]: 72
- If is simply connected, then .[1]: 71
Examples
- Let . The antipodal map with generates, together with the composition of maps, a group and induces a group action , which acts discontinuously on . Because of it follows, that the quotient map is a normal covering and for a universal covering, hence for .
- Let be the special orthogonal group, then the map is a normal covering and because of , it is the universal covering, hence .
- With the group action of on , whereby is the semidirect product , one gets the universal covering of the klein bottle , hence .
- Let be the torus which is embedded in the . Then one gets a homeomorphism , which induces a discontinuous group action , whereby . It follows, that the map is a normal covering of the klein bottle, hence .
- Let be embedded in the . Since the group action is discontinuously, whereby are coprime, the map is the universal covering of the lens space , hence .
Galois correspondence
Let be a connected and locally simply connected space, then for every subgroup there exists a path-connected covering with .[1]: 66
Let and be two path-connected coverings, then they are equivalent iff the subgroups and are conjugate to each other.[4]: 482
Let be a connected and locally simply connected space, then, up to equivalence between coverings, there is a bijection:
For a sequence of subgroups one gets a sequence of coverings . For a subgroup with index , the covering has degree .
Classification
Category of coverings
Let be a topological space. The objects of the category are the coverings of and the morphisms between two coverings and are continuous maps , such that the diagram
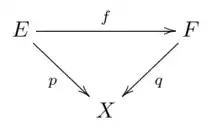
commutes.
Applications
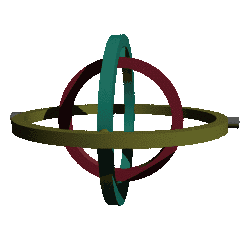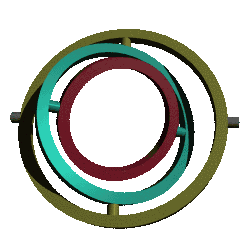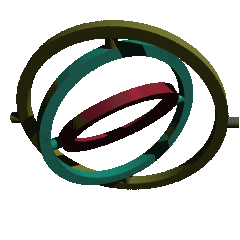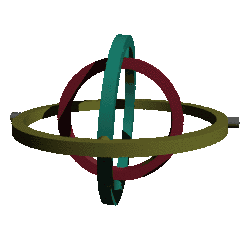
An important practical application of covering spaces occurs in charts on SO(3), the rotation group. This group occurs widely in engineering, due to 3-dimensional rotations being heavily used in navigation, nautical engineering, and aerospace engineering, among many other uses. Topologically, SO(3) is the real projective space RP3, with fundamental group Z/2, and only (non-trivial) covering space the hypersphere S3, which is the group Spin(3), and represented by the unit quaternions. Thus quaternions are a preferred method for representing spatial rotations – see quaternions and spatial rotation.
However, it is often desirable to represent rotations by a set of three numbers, known as Euler angles (in numerous variants), both because this is conceptually simpler for someone familiar with planar rotation, and because one can build a combination of three gimbals to produce rotations in three dimensions. Topologically this corresponds to a map from the 3-torus T3 of three angles to the real projective space RP3 of rotations, and the resulting map has imperfections due to this map being unable to be a covering map. Specifically, the failure of the map to be a local homeomorphism at certain points is referred to as gimbal lock, and is demonstrated in the animation at the right – at some points (when the axes are coplanar) the rank of the map is 2, rather than 3, meaning that only 2 dimensions of rotations can be realized from that point by changing the angles. This causes problems in applications, and is formalized by the notion of a covering space.
See also
- Bethe lattice is the universal cover of a Cayley graph
- Covering graph, a covering space for an undirected graph, and its special case the bipartite double cover
- Covering group
- Galois connection
- Quotient space (topology)
Literature
- Allen Hatcher: Algebraic Topology. Cambridge Univ. Press, Cambridge, ISBN 0-521-79160-X
- Otto Forster: Lectures on Riemann surfaces. Springer Berlin, München 1991, ISBN 978-3-540-90617-9
- James Munkres: Topology. Upper Saddle River, NJ: Prentice Hall, Inc., ©2000, ISBN 978-0-13-468951-7
- Wolfgang Kühnel: Matrizen und Lie-Gruppen. Springer Fachmedien Wiesbaden GmbH, Stuttgart, ISBN 978-3-8348-9905-7
References
- Hatcher, Allen (2001). Algebraic Topology. Cambridge: Cambridge Univ. Press. ISBN 0-521-79160-X.
- Kühnel, Wolfgang. Matrizen und Lie-Gruppen. Stuttgart: Springer Fachmedien Wiesbaden GmbH. ISBN 978-3-8348-9905-7.
- Forster, Otto (1991). Lectures on Riemann surfaces. München: Springer Berlin. ISBN 978-3-540-90617-9.
- Munkres, James (2000). Topology. Upper Saddle River, NJ: Prentice Hall, Inc. ISBN 978-0-13-468951-7.
- Aguilar, Marcelo Alberto; Socolovsky, Miguel (23 November 1999). "The Universal Covering Group of U(n) and Projective Representations". International Journal of Theoretical Physics. Springer US (published April 2000). 39 (4): 997–1013. arXiv:math-ph/9911028. Bibcode:1999math.ph..11028A. doi:10.1023/A:1003694206391.