Photon

A photon (from Ancient Greek φῶς, φωτός (phôs, phōtós) 'light') is an elementary particle that is a quantum of the electromagnetic field, including electromagnetic radiation such as light and radio waves, and the force carrier for the electromagnetic force. Photons are massless,[lower-alpha 1] so they always move at the speed of light in vacuum, 299792458 m/s (or about 186,282 mi/s). The photon belongs to the class of bosons.

Photon
Photons are emitted by a cyan laser beam outside, orange laser beam inside calcite and its fluorescence
CompositionElementary particle
StatisticsBosonic
FamilyGauge boson
InteractionsElectromagnetic, weak (and gravity)
Symbol γ
TheorizedAlbert Einstein (1905)
The name "photon" is generally attributed to Gilbert N. Lewis (1926)
Mass0 (theoretical value)
< 1×10−18 eV/c2 (experimental limit)[1]
Mean lifetimeStable[1]
Electric charge0
< 1×10−35 e[1]
Color charge0
Spin1
Spin states+1 ℏ,  −1 ℏ
Parity−1[1]
C parity−1[1]
CondensedI(JP C)=0,1(1−−)[1]

As with other elementary particles, photons are best explained by quantum mechanics and exhibit wave–particle duality, their behavior featuring properties of both waves and particles.[2] The modern photon concept originated during the first two decades of the 20th century with the work of Albert Einstein, who built upon the research of Max Planck. While trying to explain how matter and electromagnetic radiation could be in thermal equilibrium with one another, Planck proposed that the energy stored within a material object should be regarded as composed of an integer number of discrete, equal-sized parts. To explain the photoelectric effect, Einstein introduced the idea that light itself is made of discrete units of energy. In 1926, Gilbert N. Lewis popularized the term photon for these energy units.[3][4][5] Subsequently, many other experiments validated Einstein's approach.[6][7][8]

In the Standard Model of particle physics, photons and other elementary particles are described as a necessary consequence of physical laws having a certain symmetry at every point in spacetime. The intrinsic properties of particles, such as charge, mass, and spin, are determined by gauge symmetry. The photon concept has led to momentous advances in experimental and theoretical physics, including lasers, Bose–Einstein condensation, quantum field theory, and the probabilistic interpretation of quantum mechanics. It has been applied to photochemistry, high-resolution microscopy, and measurements of molecular distances. Moreover, photons have been studied as elements of quantum computers, and for applications in optical imaging and optical communication such as quantum cryptography.

Nomenclature
Photoelectric effect: the emission of electrons from a metal plate caused by light quanta – photons.
1926 Gilbert N. Lewis letter which brought the word "photon" into common usage

The word quanta (singular quantum, Latin for how much) was used before 1900 to mean particles or amounts of different quantities, including electricity. In 1900, the German physicist Max Planck was studying black-body radiation, and he suggested that the experimental observations, specifically at shorter wavelengths, would be explained if the energy stored within a molecule was a "discrete quantity composed of an integral number of finite equal parts", which he called "energy elements".[9] In 1905, Albert Einstein published a paper in which he proposed that many light-related phenomena—including black-body radiation and the photoelectric effect—would be better explained by modelling electromagnetic waves as consisting of spatially localized, discrete wave-packets.[10] He called such a wave-packet the light quantum (German: das Lichtquant).[lower-alpha 2]

The name photon derives from the Greek word for light, φῶς (transliterated phôs). Arthur Compton used photon in 1928, referring to G.N. Lewis, who coined the term in a letter to Nature on 18 December 1926.[3][11] The same name was used earlier but was never widely adopted before Lewis: in 1916 by the American physicist and psychologist Leonard T. Troland, in 1921 by the Irish physicist Joly, in 1924 by the French physiologist René Wurmser (1890–1993), and in 1926 by the French physicist Frithiof Wolfers (1891–1971).[5] The name was suggested initially as a unit related to the illumination of the eye and the resulting sensation of light and was used later in a physiological context. Although Wolfers's and Lewis's theories were contradicted by many experiments and never accepted, the new name was adopted by most physicists very soon after Compton used it.[5][lower-alpha 3]

In physics, a photon is usually denoted by the symbol γ (the Greek letter gamma). This symbol for the photon probably derives from gamma rays, which were discovered in 1900 by Paul Villard,[13][14] named by Ernest Rutherford in 1903, and shown to be a form of electromagnetic radiation in 1914 by Rutherford and Edward Andrade.[15] In chemistry and optical engineering, photons are usually symbolized by hν, which is the photon energy, where h is Planck constant and the Greek letter ν (nu) is the photon's frequency.[16] Much less commonly, the photon can be symbolized by hf, where its frequency is denoted by f.[17]

Physical properties

A photon is massless,[lower-alpha 4] has no electric charge,[19][20] and is a stable particle. In a vacuum, a photon has three possible polarization states.[21][lower-alpha 5] The photon is the gauge boson for electromagnetism,[22]: 29–30  and therefore all other quantum numbers of the photon (such as lepton number, baryon number, and flavour quantum numbers) are zero.[23] Also, the photon obeys Bose–Einstein statistics, and not Fermi-Dirac statistics. That is, they do not obey the Pauli exclusion principle[24]: 1221  and more than one can occupy the same bound quantum state.

Photons are emitted in many natural processes. For example, when a charge is accelerated it emits synchrotron radiation. During a molecular, atomic or nuclear transition to a lower energy level, photons of various energy will be emitted, ranging from radio waves to gamma rays. Photons can also be emitted when a particle and its corresponding antiparticle are annihilated (for example, electron–positron annihilation).[24]: 572, 1114, 1172 

Relativistic energy and momentum
See also: Special relativity
The cone shows possible values of wave 4-vector of a photon. The "time" axis gives the angular frequency (rad⋅s−1) and the "space" axis represents the angular wavenumber (rad⋅m−1). Green and indigo represent left and right polarization

In empty space, the photon moves at c (the speed of light) and its energy and momentum are related by E = p c , where p is the magnitude of the momentum vector p. This derives from the following relativistic relation, with m = 0 :[25]

The energy and momentum of a photon depend only on its frequency () or inversely, its wavelength (λ):

where k is the wave vector, where

  • k ≡ |k| =  2π /λ   is the wave number, and
  • ω ≡ 2 π ν   is the angular frequency, and
  • ħ ≡ h/ 2π    is the reduced Planck constant.[26]

Since p points in the direction of the photon's propagation, the magnitude of its momentum is

Polarization and angular momentum

The photon also carries two other quantities called spin angular momentum (which is related to linear or circular photon polarization) and orbital angular momentum.

Spin angular momentum

The spin angular momentum of light does not depend on its frequency, and was experimentally verified by Raman and Bhagavantam in 1931.[27]

Because photons always move at the speed of light, the spin is best expressed in terms of the component measured along its direction of motion, its helicity, which must be either +ħ or −ħ.[lower-alpha 5] These two possible helicities, called right-handed and left-handed, correspond to the two possible circular polarization states of the photon.[28]

To illustrate the significance of these formulae, the annihilation of a particle with its antiparticle in free space must result in the creation of at least two photons for the following reason: In the center of momentum frame, the colliding antiparticles have no net momentum, whereas a single photon always has momentum (since, as we have seen, it is determined by the photon's frequency or wavelength, which cannot be zero). Hence, conservation of momentum (or equivalently, translational invariance) requires that at least two photons are created, with zero net momentum.[lower-alpha 6][29]: 64–65  The energy of the two photons, or, equivalently, their frequency, may be determined from conservation of four-momentum.

Seen another way, the photon can be considered as its own antiparticle (thus an "antiphoton" is simply a normal photon with opposite momentum, equal polarization, and 180° out of phase). The reverse process, pair production, is the dominant mechanism by which high-energy photons such as gamma rays lose energy while passing through matter.[30] That process is the reverse of "annihilation to one photon" allowed in the electric field of an atomic nucleus.

The classical formulae for the energy and momentum of electromagnetic radiation can be re-expressed in terms of photon events. For example, the pressure of electromagnetic radiation on an object derives from the transfer of photon momentum per unit time and unit area to that object, since pressure is force per unit area and force is the change in momentum per unit time.[31]

Orbital angular momentum

Each photon carries two distinct and independent forms of angular momentum: spin and orbital angular momentum. As discussed above, the spin angular momentum of light of a particular photon is always either +ħ, 0, or −ħ.[lower-alpha 5] In contrast, the light orbital angular momentum of a particular photon can be any integer N, including zero.[32]

Experimental checks on photon mass

Current commonly accepted physical theories imply or assume the photon to be strictly massless. If the photon is not a strictly massless particle, it would not move at the exact speed of light, c, in vacuum. Its speed would be lower and depend on its frequency. Relativity would be unaffected by this; the so-called speed of light, c, would then not be the actual speed at which light moves, but a constant of nature which is the upper bound on speed that any object could theoretically attain in spacetime.[33] Thus, it would still be the speed of spacetime ripples (gravitational waves and gravitons), but it would not be the speed of photons.

If a photon did have non-zero mass, there would be other effects as well. Coulomb's law would be modified and the electromagnetic field would have an extra physical degree of freedom. These effects yield more sensitive experimental probes of the photon mass than the frequency dependence of the speed of light. If Coulomb's law is not exactly valid, then that would allow the presence of an electric field to exist within a hollow conductor when it is subjected to an external electric field. This provides a means for very-high-precision tests of Coulomb's law.[34] A null result of such an experiment has set a limit of m ≲ 10−14 eV/c2.[35]

Sharper upper limits on the mass of light have been obtained in experiments designed to detect effects caused by the galactic vector potential. Although the galactic vector potential is very large because the galactic magnetic field exists on very great length scales, only the magnetic field would be observable if the photon is massless. In the case that the photon has mass, the mass term 1/2m2AμAμ would affect the galactic plasma. The fact that no such effects are seen implies an upper bound on the photon mass of m < 3×10−27 eV/c2.[36] The galactic vector potential can also be probed directly by measuring the torque exerted on a magnetized ring.[37] Such methods were used to obtain the sharper upper limit of 1.07×10−27 eV/c2 (the equivalent of 10−36 daltons) given by the Particle Data Group.[38]

These sharp limits from the non-observation of the effects caused by the galactic vector potential have been shown to be model-dependent.[39] If the photon mass is generated via the Higgs mechanism then the upper limit of m ≲ 10−14 eV/c2 from the test of Coulomb's law is valid.

Historical development
Main article: Light
Thomas Young's double-slit experiment in 1801 showed that light can act as a wave, helping to invalidate early particle theories of light.[24]: 964 

In most theories up to the eighteenth century, light was pictured as being made up of particles. Since particle models cannot easily account for the refraction, diffraction and birefringence of light, wave theories of light were proposed by René Descartes (1637),[40] Robert Hooke (1665),[41] and Christiaan Huygens (1678);[42] however, particle models remained dominant, chiefly due to the influence of Isaac Newton.[43] In the early 19th century, Thomas Young and August Fresnel clearly demonstrated the interference and diffraction of light, and by 1850 wave models were generally accepted.[44] James Clerk Maxwell's 1865 prediction[45] that light was an electromagnetic wave – which was confirmed experimentally in 1888 by Heinrich Hertz's detection of radio waves[46] – seemed to be the final blow to particle models of light.

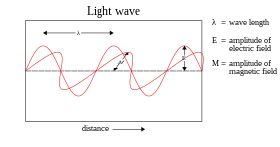
In 1900, Maxwell's theoretical model of light as oscillating electric and magnetic fields seemed complete. However, several observations could not be explained by any wave model of electromagnetic radiation, leading to the idea that light-energy was packaged into quanta described by E = hν . Later experiments showed that these light-quanta also carry momentum and, thus, can be considered particles: The photon concept was born, leading to a deeper understanding of the electric and magnetic fields themselves.

The Maxwell wave theory, however, does not account for all properties of light. The Maxwell theory predicts that the energy of a light wave depends only on its intensity, not on its frequency; nevertheless, several independent types of experiments show that the energy imparted by light to atoms depends only on the light's frequency, not on its intensity. For example, some chemical reactions are provoked only by light of frequency higher than a certain threshold; light of frequency lower than the threshold, no matter how intense, does not initiate the reaction. Similarly, electrons can be ejected from a metal plate by shining light of sufficiently high frequency on it (the photoelectric effect); the energy of the ejected electron is related only to the light's frequency, not to its intensity.[47][lower-alpha 7]

At the same time, investigations of black-body radiation carried out over four decades (1860–1900) by various researchers[49] culminated in Max Planck's hypothesis[50][51] that the energy of any system that absorbs or emits electromagnetic radiation of frequency ν is an integer multiple of an energy quantum E = hν . As shown by Albert Einstein,[10][52] some form of energy quantization must be assumed to account for the thermal equilibrium observed between matter and electromagnetic radiation; for this explanation of the photoelectric effect, Einstein received the 1921 Nobel Prize in physics.[53]

Since the Maxwell theory of light allows for all possible energies of electromagnetic radiation, most physicists assumed initially that the energy quantization resulted from some unknown constraint on the matter that absorbs or emits the radiation. In 1905, Einstein was the first to propose that energy quantization was a property of electromagnetic radiation itself.[10] Although he accepted the validity of Maxwell's theory, Einstein pointed out that many anomalous experiments could be explained if the energy of a Maxwellian light wave were localized into point-like quanta that move independently of one another, even if the wave itself is spread continuously over space.[10] In 1909[52] and 1916,[54] Einstein showed that, if Planck's law regarding black-body radiation is accepted, the energy quanta must also carry momentum p =  h / λ  , making them full-fledged particles. This photon momentum was observed experimentally by Arthur Compton,[55] for which he received the Nobel Prize in 1927. The pivotal question then, was how to unify Maxwell's wave theory of light with its experimentally observed particle nature? The answer to this question occupied Albert Einstein for the rest of his life,[56] and was solved in quantum electrodynamics and its successor, the Standard Model. (See § Second quantization and § As a gauge boson, below.)

Up to 1923, most physicists were reluctant to accept that light itself was quantized. Instead, they tried to explain photon behaviour by quantizing only matter, as in the Bohr model of the hydrogen atom (shown here). Even though these semiclassical models were only a first approximation, they were accurate for simple systems and they led to quantum mechanics.

Einstein's 1905 predictions were verified experimentally in several ways in the first two decades of the 20th century, as recounted in Robert Millikan's Nobel lecture.[57] However, before Compton's experiment[55] showed that photons carried momentum proportional to their wave number (1922), most physicists were reluctant to believe that electromagnetic radiation itself might be particulate. (See, for example, the Nobel lectures of Wien,[49] Planck[51] and Millikan.)[57] Instead, there was a widespread belief that energy quantization resulted from some unknown constraint on the matter that absorbed or emitted radiation. Attitudes changed over time. In part, the change can be traced to experiments such as those revealing Compton scattering, where it was much more difficult not to ascribe quantization to light itself to explain the observed results.[58]

Even after Compton's experiment, Niels Bohr, Hendrik Kramers and John Slater made one last attempt to preserve the Maxwellian continuous electromagnetic field model of light, the so-called BKS theory.[59] An important feature of the BKS theory is how it treated the conservation of energy and the conservation of momentum. In the BKS theory, energy and momentum are only conserved on the average across many interactions between matter and radiation. However, refined Compton experiments showed that the conservation laws hold for individual interactions.[60] Accordingly, Bohr and his co-workers gave their model "as honorable a funeral as possible".[56] Nevertheless, the failures of the BKS model inspired Werner Heisenberg in his development of matrix mechanics.[61]

A few physicists persisted[62] in developing semiclassical models in which electromagnetic radiation is not quantized, but matter appears to obey the laws of quantum mechanics. Although the evidence from chemical and physical experiments for the existence of photons was overwhelming by the 1970s, this evidence could not be considered as absolutely definitive; since it relied on the interaction of light with matter, and a sufficiently complete theory of matter could in principle account for the evidence. Nevertheless, all semiclassical theories were refuted definitively in the 1970s and 1980s by photon-correlation experiments.[lower-alpha 8] Hence, Einstein's hypothesis that quantization is a property of light itself is considered to be proven.

Wave–particle duality and uncertainty principles
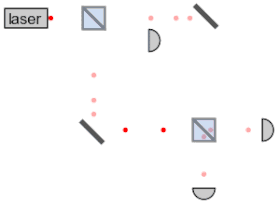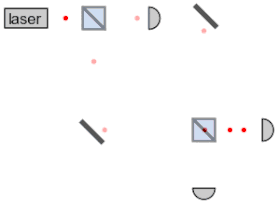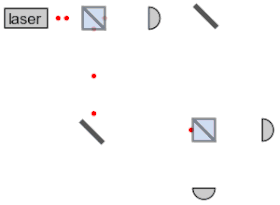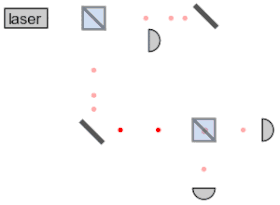
Photons in a Mach–Zehnder interferometer exhibit wave-like interference and particle-like detection at single-photon detectors.

Photons obey the laws of quantum mechanics, and so their behavior has both wave-like and particle-like aspects. When a photon is detected by a measuring instrument, it is registered as a single, particulate unit. However, the probability of detecting a photon is calculated by equations that describe waves. This combination of aspects is known as wave–particle duality. For example, the probability distribution for the location at which a photon might be detected displays clearly wave-like phenomena such as diffraction and interference. A single photon passing through a double slit has its energy received at a point on the screen with a probability distribution given by its interference pattern determined by Maxwell's wave equations.[65] However, experiments confirm that the photon is not a short pulse of electromagnetic radiation; a photon's Maxwell waves will diffract, but photon energy does not spread out as it propagates, nor does this energy divide when it encounters a beam splitter.[66] Rather, the received photon acts like a point-like particle since it is absorbed or emitted as a whole by arbitrarily small systems, including systems much smaller than its wavelength, such as an atomic nucleus (≈10−15 m across) or even the point-like electron.

While many introductory texts treat photons using the mathematical techniques of non-relativistic quantum mechanics, this is in some ways an awkward oversimplification, as photons are by nature intrinsically relativistic. Because photons have zero rest mass, no wave function defined for a photon can have all the properties familiar from wave functions in non-relativistic quantum mechanics.[lower-alpha 9] In order to avoid these difficulties, physicists employ the second-quantized theory of photons described below, quantum electrodynamics, in which photons are quantized excitations of electromagnetic modes.[71]

Another difficulty is finding the proper analogue for the uncertainty principle, an idea frequently attributed to Heisenberg, who introduced the concept in analyzing a thought experiment involving an electron and a high-energy photon. However, Heisenberg did not give precise mathematical definitions of what the "uncertainty" in these measurements meant. The precise mathematical statement of the position–momentum uncertainty principle is due to Kennard, Pauli, and Weyl.[72][73] The uncertainty principle applies to situations where an experimenter has a choice of measuring either one of two "canonically conjugate" quantities, like the position and the momentum of a particle. According to the uncertainty principle, no matter how the particle is prepared, it is not possible to make a precise prediction for both of the two alternative measurements: if the outcome of the position measurement is made more certain, the outcome of the momentum measurement becomes less so, and vice versa.[74] A coherent state minimizes the overall uncertainty as far as quantum mechanics allows.[71] Quantum optics makes use of coherent states for modes of the electromagnetic field. There is a tradeoff, reminiscent of the position–momentum uncertainty relation, between measurements of an electromagnetic wave's amplitude and its phase.[71] This is sometimes informally expressed in terms of the uncertainty in the number of photons present in the electromagnetic wave, , and the uncertainty in the phase of the wave, . However, this cannot be an uncertainty relation of the Kennard–Pauli–Weyl type, since unlike position and momentum, the phase cannot be represented by a Hermitian operator.[75]

Bose–Einstein model of a photon gas
Main articles: Bose gas, Bose–Einstein statistics, Spin-statistics theorem, Gas in a box, and Photon gas

In 1924, Satyendra Nath Bose derived Planck's law of black-body radiation without using any electromagnetism, but rather by using a modification of coarse-grained counting of phase space.[76] Einstein showed that this modification is equivalent to assuming that photons are rigorously identical and that it implied a "mysterious non-local interaction",[77][78] now understood as the requirement for a symmetric quantum mechanical state. This work led to the concept of coherent states and the development of the laser. In the same papers, Einstein extended Bose's formalism to material particles (bosons) and predicted that they would condense into their lowest quantum state at low enough temperatures; this Bose–Einstein condensation was observed experimentally in 1995.[79] It was later used by Lene Hau to slow, and then completely stop, light in 1999[80] and 2001.[81]

The modern view on this is that photons are, by virtue of their integer spin, bosons (as opposed to fermions with half-integer spin). By the spin-statistics theorem, all bosons obey Bose–Einstein statistics (whereas all fermions obey Fermi–Dirac statistics).[82]

Stimulated and spontaneous emission
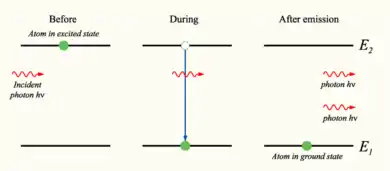
Main articles: Stimulated emission and Laser
Stimulated emission (in which photons "clone" themselves) was predicted by Einstein in his kinetic analysis, and led to the development of the laser. Einstein's derivation inspired further developments in the quantum treatment of light, which led to the statistical interpretation of quantum mechanics.

In 1916, Albert Einstein showed that Planck's radiation law could be derived from a semi-classical, statistical treatment of photons and atoms, which implies a link between the rates at which atoms emit and absorb photons. The condition follows from the assumption that functions of the emission and absorption of radiation by the atoms are independent of each other, and that thermal equilibrium is made by way of the radiation's interaction with the atoms. Consider a cavity in thermal equilibrium with all parts of itself and filled with electromagnetic radiation and that the atoms can emit and absorb that radiation. Thermal equilibrium requires that the energy density of photons with frequency (which is proportional to their number density) is, on average, constant in time; hence, the rate at which photons of any particular frequency are emitted must equal the rate at which they are absorbed.[83]

Einstein began by postulating simple proportionality relations for the different reaction rates involved. In his model, the rate for a system to absorb a photon of frequency and transition from a lower energy to a higher energy is proportional to the number of atoms with energy and to the energy density of ambient photons of that frequency,

where is the rate constant for absorption. For the reverse process, there are two possibilities: spontaneous emission of a photon, or the emission of a photon initiated by the interaction of the atom with a passing photon and the return of the atom to the lower-energy state. Following Einstein's approach, the corresponding rate for the emission of photons of frequency and transition from a higher energy to a lower energy is

where is the rate constant for emitting a photon spontaneously, and is the rate constant for emissions in response to ambient photons (induced or stimulated emission). In thermodynamic equilibrium, the number of atoms in state and those in state must, on average, be constant; hence, the rates and must be equal. Also, by arguments analogous to the derivation of Boltzmann statistics, the ratio of and is where and are the degeneracy of the state and that of , respectively, and their energies, the Boltzmann constant and the system's temperature. From this, it is readily derived that and

The and are collectively known as the Einstein coefficients.[84]

Einstein could not fully justify his rate equations, but claimed that it should be possible to calculate the coefficients , and once physicists had obtained "mechanics and electrodynamics modified to accommodate the quantum hypothesis".[85] Not long thereafter, in 1926, Paul Dirac derived the rate constants by using a semiclassical approach,[86] and, in 1927, succeeded in deriving all the rate constants from first principles within the framework of quantum theory.[87][88] Dirac's work was the foundation of quantum electrodynamics, i.e., the quantization of the electromagnetic field itself. Dirac's approach is also called second quantization or quantum field theory;[89][90][91] earlier quantum mechanical treatments only treat material particles as quantum mechanical, not the electromagnetic field.

Einstein was troubled by the fact that his theory seemed incomplete, since it did not determine the direction of a spontaneously emitted photon. A probabilistic nature of light-particle motion was first considered by Newton in his treatment of birefringence and, more generally, of the splitting of light beams at interfaces into a transmitted beam and a reflected beam. Newton hypothesized that hidden variables in the light particle determined which of the two paths a single photon would take.[43] Similarly, Einstein hoped for a more complete theory that would leave nothing to chance, beginning his separation[56] from quantum mechanics. Ironically, Max Born's probabilistic interpretation of the wave function[92][93] was inspired by Einstein's later work searching for a more complete theory.[94]

Quantum field theory

Quantization of the electromagnetic field
Main article: Quantum field theory
Different electromagnetic modes (such as those depicted here) can be treated as independent simple harmonic oscillators. A photon corresponds to a unit of energy E = hν in its electromagnetic mode.

In 1910, Peter Debye derived Planck's law of black-body radiation from a relatively simple assumption.[95] He decomposed the electromagnetic field in a cavity into its Fourier modes, and assumed that the energy in any mode was an integer multiple of , where is the frequency of the electromagnetic mode. Planck's law of black-body radiation follows immediately as a geometric sum. However, Debye's approach failed to give the correct formula for the energy fluctuations of black-body radiation, which were derived by Einstein in 1909.[52]

In 1925, Born, Heisenberg and Jordan reinterpreted Debye's concept in a key way.[96] As may be shown classically, the Fourier modes of the electromagnetic field—a complete set of electromagnetic plane waves indexed by their wave vector k and polarization state—are equivalent to a set of uncoupled simple harmonic oscillators. Treated quantum mechanically, the energy levels of such oscillators are known to be , where is the oscillator frequency. The key new step was to identify an electromagnetic mode with energy as a state with photons, each of energy . This approach gives the correct energy fluctuation formula.

Feynman diagram of two electrons interacting by exchange of a virtual photon.

Dirac took this one step further.[87][88] He treated the interaction between a charge and an electromagnetic field as a small perturbation that induces transitions in the photon states, changing the numbers of photons in the modes, while conserving energy and momentum overall. Dirac was able to derive Einstein's and coefficients from first principles, and showed that the Bose–Einstein statistics of photons is a natural consequence of quantizing the electromagnetic field correctly (Bose's reasoning went in the opposite direction; he derived Planck's law of black-body radiation by assuming B–E statistics). In Dirac's time, it was not yet known that all bosons, including photons, must obey Bose–Einstein statistics.

Dirac's second-order perturbation theory can involve virtual photons, transient intermediate states of the electromagnetic field; the static electric and magnetic interactions are mediated by such virtual photons. In such quantum field theories, the probability amplitude of observable events is calculated by summing over all possible intermediate steps, even ones that are unphysical; hence, virtual photons are not constrained to satisfy , and may have extra polarization states; depending on the gauge used, virtual photons may have three or four polarization states, instead of the two states of real photons. Although these transient virtual photons can never be observed, they contribute measurably to the probabilities of observable events.[97] Indeed, such second-order and higher-order perturbation calculations can give apparently infinite contributions to the sum. Such unphysical results are corrected for using the technique of renormalization.[98]

Other virtual particles may contribute to the summation as well; for example, two photons may interact indirectly through virtual electron–positron pairs.[99] Such photon–photon scattering (see two-photon physics), as well as electron–photon scattering, is meant to be one of the modes of operations of the planned particle accelerator, the International Linear Collider.[100]

In modern physics notation, the quantum state of the electromagnetic field is written as a Fock state, a tensor product of the states for each electromagnetic mode

where represents the state in which photons are in the mode . In this notation, the creation of a new photon in mode (e.g., emitted from an atomic transition) is written as . This notation merely expresses the concept of Born, Heisenberg and Jordan described above, and does not add any physics.

As a gauge boson
Main article: Gauge theory

The electromagnetic field can be understood as a gauge field, i.e., as a field that results from requiring that a gauge symmetry holds independently at every position in spacetime.[101] For the electromagnetic field, this gauge symmetry is the Abelian U(1) symmetry of complex numbers of absolute value 1, which reflects the ability to vary the phase of a complex field without affecting observables or real valued functions made from it, such as the energy or the Lagrangian.

The quanta of an Abelian gauge field must be massless, uncharged bosons, as long as the symmetry is not broken; hence, the photon is predicted to be massless, and to have zero electric charge and integer spin. The particular form of the electromagnetic interaction specifies that the photon must have spin ±1; thus, its helicity must be . These two spin components correspond to the classical concepts of right-handed and left-handed circularly polarized light. However, the transient virtual photons of quantum electrodynamics may also adopt unphysical polarization states.[101]

In the prevailing Standard Model of physics, the photon is one of four gauge bosons in the electroweak interaction; the other three are denoted W+, W− and Z0 and are responsible for the weak interaction. Unlike the photon, these gauge bosons have mass, owing to a mechanism that breaks their SU(2) gauge symmetry. The unification of the photon with W and Z gauge bosons in the electroweak interaction was accomplished by Sheldon Glashow, Abdus Salam and Steven Weinberg, for which they were awarded the 1979 Nobel Prize in physics.[102][103][104] Physicists continue to hypothesize grand unified theories that connect these four gauge bosons with the eight gluon gauge bosons of quantum chromodynamics; however, key predictions of these theories, such as proton decay, have not been observed experimentally.[105]

Hadronic properties

Measurements of the interaction between energetic photons and hadrons show that the interaction is much more intense than expected by the interaction of merely photons with the hadron's electric charge. Furthermore, the interaction of energetic photons with protons is similar to the interaction of photons with neutrons[106] in spite of the fact that the electric charge structures of protons and neutrons are substantially different. A theory called Vector Meson Dominance (VMD) was developed to explain this effect. According to VMD, the photon is a superposition of the pure electromagnetic photon which interacts only with electric charges and vector mesons.[107] However, if experimentally probed at very short distances, the intrinsic structure of the photon is recognized as a flux of quark and gluon components, quasi-free according to asymptotic freedom in QCD and described by the photon structure function.[108][109] A comprehensive comparison of data with theoretical predictions was presented in a review in 2000.[110]

Contributions to the mass of a system

The energy of a system that emits a photon is decreased by the energy of the photon as measured in the rest frame of the emitting system, which may result in a reduction in mass in the amount . Similarly, the mass of a system that absorbs a photon is increased by a corresponding amount. As an application, the energy balance of nuclear reactions involving photons is commonly written in terms of the masses of the nuclei involved, and terms of the form for the gamma photons (and for other relevant energies, such as the recoil energy of nuclei).[111]

This concept is applied in key predictions of quantum electrodynamics (QED, see above). In that theory, the mass of electrons (or, more generally, leptons) is modified by including the mass contributions of virtual photons, in a technique known as renormalization. Such "radiative corrections" contribute to a number of predictions of QED, such as the magnetic dipole moment of leptons, the Lamb shift, and the hyperfine structure of bound lepton pairs, such as muonium and positronium.[112]

Since photons contribute to the stress–energy tensor, they exert a gravitational attraction on other objects, according to the theory of general relativity. Conversely, photons are themselves affected by gravity; their normally straight trajectories may be bent by warped spacetime, as in gravitational lensing, and their frequencies may be lowered by moving to a higher gravitational potential, as in the Pound–Rebka experiment. However, these effects are not specific to photons; exactly the same effects would be predicted for classical electromagnetic waves.[113]

In matter

Light that travels through transparent matter does so at a lower speed than c, the speed of light in a vacuum. The factor by which the speed is decreased is called the refractive index of the material. In a classical wave picture, the slowing can be explained by the light inducing electric polarization in the matter, the polarized matter radiating new light, and that new light interfering with the original light wave to form a delayed wave. In a particle picture, the slowing can instead be described as a blending of the photon with quantum excitations of the matter to produce quasi-particles known as polariton (see this list for some other quasi-particles); this polariton has a nonzero effective mass, which means that it cannot travel at c. Light of different frequencies may travel through matter at different speeds; this is called dispersion (not to be confused with scattering). In some cases, it can result in extremely slow speeds of light in matter. The effects of photon interactions with other quasi-particles may be observed directly in Raman scattering and Brillouin scattering.[114]

Photons can be scattered by matter. For example, photons engage in so many collisions on the way from the core of the Sun that radiant energy can take about a million years to reach the surface;[115] however, once in open space, a photon takes only 8.3 minutes to reach Earth.[116]

Photons can also be absorbed by nuclei, atoms or molecules, provoking transitions between their energy levels. A classic example is the molecular transition of retinal (C20H28O), which is responsible for vision, as discovered in 1958 by Nobel laureate biochemist George Wald and co-workers. The absorption provokes a cis–trans isomerization that, in combination with other such transitions, is transduced into nerve impulses. The absorption of photons can even break chemical bonds, as in the photodissociation of chlorine; this is the subject of photochemistry.[117][118]

Technological applications

Photons have many applications in technology. These examples are chosen to illustrate applications of photons per se, rather than general optical devices such as lenses, etc. that could operate under a classical theory of light. The laser is an extremely important application and is discussed above under stimulated emission.

Individual photons can be detected by several methods. The classic photomultiplier tube exploits the photoelectric effect: a photon of sufficient energy strikes a metal plate and knocks free an electron, initiating an ever-amplifying avalanche of electrons. Semiconductor charge-coupled device chips use a similar effect: an incident photon generates a charge on a microscopic capacitor that can be detected. Other detectors such as Geiger counters use the ability of photons to ionize gas molecules contained in the device, causing a detectable change of conductivity of the gas.[119]

Planck's energy formula is often used by engineers and chemists in design, both to compute the change in energy resulting from a photon absorption and to determine the frequency of the light emitted from a given photon emission. For example, the emission spectrum of a gas-discharge lamp can be altered by filling it with (mixtures of) gases with different electronic energy level configurations.[120]

Under some conditions, an energy transition can be excited by "two" photons that individually would be insufficient. This allows for higher resolution microscopy, because the sample absorbs energy only in the spectrum where two beams of different colors overlap significantly, which can be made much smaller than the excitation volume of a single beam (see two-photon excitation microscopy). Moreover, these photons cause less damage to the sample, since they are of lower energy.[121]

In some cases, two energy transitions can be coupled so that, as one system absorbs a photon, another nearby system "steals" its energy and re-emits a photon of a different frequency. This is the basis of fluorescence resonance energy transfer, a technique that is used in molecular biology to study the interaction of suitable proteins.[122]

Several different kinds of hardware random number generators involve the detection of single photons. In one example, for each bit in the random sequence that is to be produced, a photon is sent to a beam-splitter. In such a situation, there are two possible outcomes of equal probability. The actual outcome is used to determine whether the next bit in the sequence is "0" or "1".[123][124]

Quantum optics and computation

Much research has been devoted to applications of photons in the field of quantum optics. Photons seem well-suited to be elements of an extremely fast quantum computer, and the quantum entanglement of photons is a focus of research. Nonlinear optical processes are another active research area, with topics such as two-photon absorption, self-phase modulation, modulational instability and optical parametric oscillators. However, such processes generally do not require the assumption of photons per se; they may often be modeled by treating atoms as nonlinear oscillators. The nonlinear process of spontaneous parametric down conversion is often used to produce single-photon states. Finally, photons are essential in some aspects of optical communication, especially for quantum cryptography.[125]

Two-photon physics studies interactions between photons, which are rare. In 2018, MIT researchers announced the discovery of bound photon triplets, which may involve polaritons.[126][127]

See also

Notes
  1. The photon's invariant mass (also called "rest mass" for massive particles) is believed to be exactly zero. This is the notion of particle mass generally used by modern physicists. The photon does have a nonzero relativistic mass, depending on its energy, but this varies according to the frame of reference.
  2. Although the 1967 Elsevier translation of Planck's Nobel Lecture interprets Planck's Lichtquant as "photon", the more literal 1922 translation by Hans Thacher Clarke and Ludwik Silberstein Planck, Max (1922). "via Google Books". The Origin and Development of the Quantum Theory. Clarendon Press – via Internet Archive (archive.org, 2007-03-01). uses "light-quantum". No evidence is known that Planck himself had used the term "photon" as of 1926 (see also).
  3. Asimov[12] credits Arthur Compton with defining quanta of energy as photons in 1923.[12]
  4. The mass of the photon is believed to be exactly zero. Some sources also refer to the relativistic mass, which is just the energy rescaled to units of mass. For a photon with wavelength λ or energy E, this pseudo-mass “ᵯ” is given by ᵯ = h/ λc  , or ᵯ = E / c² . This use of the term “mass” is now considered exotic, and no longer common in scientific literature.[18]
  5. The possible spin states of a spin J = 1 boson are +1, 0, and −1. Spins +1 and −1 are the distinct circularly polarized states. Also, it can be introduced 'zero' spin: the spin state = 0 case can be interpreted as a linearly polarized wave, with no circular polarization, or equivalently as a superposition of two +1 and −1 circular states. See Photon polarization.
  6. However, it is possible if the system interacts with a third particle or field for the annihilation to produce one photon, since the third particle or field can absorb momentum equal and opposite to the single photon, providing dynamic balance. An example is when a positron annihilates with a bound atomic electron; in that case, it is possible for only one photon to be emitted, as the nuclear Coulomb field breaks translational symmetry.
  7. The phrase "no matter how intense" refers to intensities below approximately 1013 W/cm2 at which point perturbation theory begins to break down. In contrast, in the intense regime, which for visible light is above approximately 1014 W/cm2, the classical wave description correctly predicts the energy acquired by electrons, called ponderomotive energy.[48] By comparison, sunlight is only about 0.1 W/cm2.
  8. These experiments produce results that cannot be explained by any classical theory of light, since they involve anticorrelations that result from the quantum measurement process. In 1974, the first such experiment was carried out by Clauser, who reported a violation of a classical Cauchy–Schwarz inequality. In 1977, Kimble et al. demonstrated an analogous anti-bunching effect of photons interacting with a beam splitter; this approach was simplified and sources of error eliminated in the photon-anticorrelation experiment of Grangier, Roger, & Aspect (1986);[63] This work is reviewed and simplified further in Thorn, Neel, et al. (2004).[64]
  9. The issue was first formulated by Theodore Duddell Newton and Eugene Wigner.[67][68][69] The challenges arise from the fundamental nature of the Lorentz group, which describes the symmetries of spacetime in special relativity. Unlike the generators of Galilean transformations, the generators of Lorentz boosts do not commute, and so simultaneously assigning low uncertainties to all coordinates of a relativistic particle's position becomes problematic.[70]

    References
    1. Amsler, C.; et al. (Particle Data Group) (2008). "Review of Particle Physics: Gauge and Higgs bosons" (PDF). Physics Letters B. 667 (1): 1. Bibcode:2008PhLB..667....1A. doi:10.1016/j.physletb.2008.07.018. hdl:1854/LU-685594. S2CID 227119789.
    2. Joos, George (1951). Theoretical Physics. London and Glasgow: Blackie and Son Limited. p. 679.
    3. "December 18, 1926: Gilbert Lewis coins "photon" in letter to Nature". www.aps.org. Retrieved 2019-03-09.
    4. "Gilbert N. Lewis". Atomic Heritage Foundation. Retrieved 2019-03-09.
    5. Kragh, Helge (2014). "Photon: New light on an old name". arXiv:1401.0293 [physics.hist-ph].
    6. Compton, Arthur H. (1965) [12 Dec 1927]. "X-rays as a branch of optics" (PDF). From Nobel Lectures, Physics 1922–1941. Amsterdam: Elsevier Publishing Company.
    7. Kimble, H.J.; Dagenais, M.; Mandel, L. (1977). "Photon Anti-bunching in Resonance Fluorescence" (PDF). Physical Review Letters. 39 (11): 691–695. Bibcode:1977PhRvL..39..691K. doi:10.1103/PhysRevLett.39.691.
    8. Grangier, P.; Roger, G.; Aspect, A. (1986). "Experimental Evidence for a Photon Anticorrelation Effect on a Beam Splitter: A New Light on Single-Photon Interferences". Europhysics Letters. 1 (4): 173–179. Bibcode:1986EL......1..173G. CiteSeerX 10.1.1.178.4356. doi:10.1209/0295-5075/1/4/004. S2CID 250837011.
    9. Kragh, Helge (2000-12-01). "Max Planck: the reluctant revolutionary". Physics World. 13 (12): 31–36. doi:10.1088/2058-7058/13/12/34.
    10. Einstein, A. (1905). "Über einen die Erzeugung und Verwandlung des Lichtes betreffenden heuristischen Gesichtspunkt" (PDF). Annalen der Physik (in German). 17 (6): 132–148. Bibcode:1905AnP...322..132E. doi:10.1002/andp.19053220607.. An English translation is available from Wikisource.
    11. Lewis, G.N. (18 December 1926). "The conservation of photons". Nature. 118 (2981): 874–875. Bibcode:1926Natur.118..874L. doi:10.1038/118874a0. eISSN 1476-4687. S2CID 4110026. see also
      "Discordances entre l'expérience et la théorie électromagnétique du rayonnement". Written at Bruxelles, BE. Electrons et photons: Rapports et discussions du cinquième Conseil de Physique tenu à Bruxelles du 24 au 29 octobre 1927 sous les auspices de l'Institut International de Physique Solvay. Cinquième Conseil de Physique (in French). l'Institut International de Physique Solvay (host institution). Paris, FR: Gauthier-Villars et Cie (published 1928). 24–29 October 1927. pp. 55–85.{{cite conference}}: CS1 maint: others (link)
    12. Asimov, Isaac (1983). The Neutrino: Ghost particle of the atom. Garden City, NY: Avon Books. ISBN 978-0-380-00483-6. and
      Asimov, Isaac (1971). The Universe: From flat Earth to quasar. New York: Walker. ISBN 978-0-8027-0316-3. LCCN 66022515.
    13. Villard, P. (1900). "Sur la réflexion et la réfraction des rayons cathodiques et des rayons déviables du radium". Comptes Rendus des Séances de l'Académie des Sciences (in French). 130: 1010–1012.
    14. Villard, P. (1900). "Sur le rayonnement du radium". Comptes Rendus des Séances de l'Académie des Sciences (in French). 130: 1178–1179.
    15. Rutherford, E.; Andrade, E.N.C. (1914). "The wavelength of the soft gamma rays from Radium B". Philosophical Magazine. 27 (161): 854–868. doi:10.1080/14786440508635156.
    16. Andrew Liddle (2015). An Introduction to Modern Cosmology. John Wiley & Sons. p. 16. ISBN 978-1-118-69025-3.
    17. SantoPietro, David. "Photon Energy". Khan Academy. Retrieved 2020-03-15.
    18. For further info see Baez, John. "What is the mass of a photon?" (pers. academic site). U.C. Riverside.
    19. Frisch, David H.; Thorndike, Alan M. (1964). Elementary Particles. Princeton, NJ: David Van Nostrand. p. 22.
    20. Kobychev, V.V.; Popov, S.B. (2005). "Constraints on the photon charge from observations of extragalactic sources". Astronomy Letters. 31 (3): 147–151. arXiv:hep-ph/0411398. Bibcode:2005AstL...31..147K. doi:10.1134/1.1883345. S2CID 119409823.
    21. Schwartz, Matthew D. (2014). Quantum Field Theory and the Standard Model. Cambridge University Press. p. 66. ISBN 978-1-107-03473-0.
    22. "Role as gauge boson and polarization" §5.1 in Aitchison, I.J.R.; Hey, A.J.G. (1993). Gauge Theories in Particle Physics. IOP Publishing. ISBN 978-0-85274-328-7.
    23. Amsler, C.; et al. (2008). "Review of Particle Physics" (PDF). Physics Letters B. 667 (1–5): 31. Bibcode:2008PhLB..667....1A. doi:10.1016/j.physletb.2008.07.018. hdl:1854/LU-685594. PMID 10020536. S2CID 227119789.
    24. Halliday, David; Resnick, Robert; Walker, Jerl (2005). Fundamental of Physics (7th ed.). John Wiley and Sons, Inc. ISBN 978-0-471-23231-5.
    25. See section 1.6 in Alonso & Finn 1968, Section 1.6
    26. Soper, Davison E. "Electromagnetic radiation is made of photons". Institute of Theoretical Science. University of Oregon.
    27. Raman, C.V.; Bhagavantam, S. (1931). "Experimental proof of the spin of the photon" (PDF). Indian Journal of Physics. 6 (3244): 353. Bibcode:1932Natur.129...22R. doi:10.1038/129022a0. hdl:10821/664. S2CID 4064852. Archived from the original (PDF) on 2016-06-03. Retrieved 2008-12-28.
    28. Burgess, C.; Moore, G. (2007). "1.3.3.2". The Standard Model: A Primer. Cambridge University Press. p. 27. ISBN 978-0-521-86036-9 – via Google Books.
    29. Griffiths, David J. (2008). Introduction to Elementary Particles (2nd revised ed.). WILEY-VCH. ISBN 978-3-527-40601-2.
    30. Alonso & Finn 1968, Section 9.3
    31. Born, Max; Blin-Stoyle, Roger John; Radcliffe, J.M. (1989). "Appendix XXXII". Atomic Physics. Courier Corporation. ISBN 978-0-486-65984-8.
    32. Willner, Alan E. (4 August 2016). "Twisted light could dramatically boost data rates: Orbital angular momentum could take optical and radio communication to new heights". IEEE Spectrum.
    33. Mermin, David (February 1984). "Relativity without light". American Journal of Physics. 52 (2): 119–124. Bibcode:1984AmJPh..52..119M. doi:10.1119/1.13917.
    34. Plimpton, S.; Lawton, W. (1936). "A Very Accurate Test of Coulomb's Law of Force Between Charges". Physical Review. 50 (11): 1066. Bibcode:1936PhRv...50.1066P. doi:10.1103/PhysRev.50.1066.
    35. Williams, E.; Faller, J.; Hill, H. (1971). "New Experimental Test of Coulomb's Law: A Laboratory Upper Limit on the Photon Rest Mass". Physical Review Letters. 26 (12): 721. Bibcode:1971PhRvL..26..721W. doi:10.1103/PhysRevLett.26.721.
    36. Chibisov, G V (1976). "Astrophysical upper limits on the photon rest mass". Soviet Physics Uspekhi. 19 (7): 624. Bibcode:1976SvPhU..19..624C. doi:10.1070/PU1976v019n07ABEH005277.
    37. Lakes, Roderic (1998). "Experimental Limits on the Photon Mass and Cosmic Magnetic Vector Potential". Physical Review Letters. 80 (9): 1826. Bibcode:1998PhRvL..80.1826L. doi:10.1103/PhysRevLett.80.1826.
    38. Amsler, C; Doser, M; Antonelli, M; Asner, D; Babu, K; Baer, H; Band, H; Barnett, R; et al. (2008). "Review of Particle Physics⁎" (PDF). Physics Letters B. 667 (1–5): 1. Bibcode:2008PhLB..667....1A. doi:10.1016/j.physletb.2008.07.018. hdl:1854/LU-685594. S2CID 227119789. Summary Table
    39. Adelberger, Eric; Dvali, Gia; Gruzinov, Andrei (2007). "Photon-Mass Bound Destroyed by Vortices". Physical Review Letters. 98 (1): 010402. arXiv:hep-ph/0306245. Bibcode:2007PhRvL..98a0402A. doi:10.1103/PhysRevLett.98.010402. PMID 17358459. S2CID 31249827.
    40. Descartes, R. (1637). Discours de la méthode (Discourse on Method) (in French). Imprimerie de Ian Maire. ISBN 978-0-268-00870-3.
    41. Hooke, R. (1667). Micrographia: or some physiological descriptions of minute bodies made by magnifying glasses with observations and inquiries thereupon ... London, UK: Royal Society of London. ISBN 978-0-486-49564-4.
    42. Huygens, C. (1678). Traité de la lumière (in French).. An English translation is available from Project Gutenberg
    43. Newton, I. (1952) [1730]. Opticks (4th ed.). Dover, NY: Dover Publications. Book II, Part III, Propositions XII–XX; Queries 25–29. ISBN 978-0-486-60205-9.
    44. Buchwald, J.Z. (1989). The Rise of the Wave Theory of Light: Optical theory and experiment in the early nineteenth century. Physics Today. Vol. 43. University of Chicago Press. pp. 78–80. Bibcode:1990PhT....43d..78B. doi:10.1063/1.2810533. ISBN 978-0-226-07886-1. OCLC 18069573.
    45. Maxwell, J.C. (1865). "A Dynamical Theory of the Electromagnetic Field". Philosophical Transactions of the Royal Society. 155: 459–512. Bibcode:1865RSPT..155..459C. doi:10.1098/rstl.1865.0008. S2CID 186207827. This article followed a presentation by Maxwell on 8 December 1864 to the Royal Society.
    46. Hertz, H. (1888). "Über Strahlen elektrischer Kraft". Sitzungsberichte der Preussischen Akademie der Wissenschaften (in German). Berlin, DE. 1888: 1297–1307.
    47. "Frequency-dependence of luminiscence" pp. 276ff., §1.4 "photoelectric effect" in Alonso & Finn 1968
    48. See also: Boreham, Bruce W.; Hora, Heinrich; Bolton, Paul R. (1996). "Photon density and the correspondence principle of electromagnetic interaction". AIP Conference Proceedings. 369: 1234–1243. Bibcode:1996AIPC..369.1234B. doi:10.1063/1.50410.
    49. Wien, W. (1911). "Wilhelm Wien Nobel Lecture". nobelprize.org.
    50. Planck, M. (1901). "Über das Gesetz der Energieverteilung im Normalspectrum". Annalen der Physik (in German). 4 (3): 553–563. Bibcode:1901AnP...309..553P. doi:10.1002/andp.19013090310. English translation
    51. Planck, M. (1920). "Max Planck's Nobel Lecture". nobelprize.org.
    52. Einstein, A. (1909). "Über die Entwicklung unserer Anschauungen über das Wesen und die Konstitution der Strahlung" (PDF). Physikalische Zeitschrift (in German). 10: 817–825.. An English translation is available from Wikisource.
    53. Presentation speech by Svante Arrhenius for the 1921 Nobel Prize in Physics, December 10, 1922. Online text from [nobelprize.org], The Nobel Foundation 2008. Access date 2008-12-05.
    54. Einstein, A. (1916). "Zur Quantentheorie der Strahlung". Mitteilungen der Physikalischen Gesellschaft zu Zürich. 16: 47. Also Physikalische Zeitschrift, 18, 121–128 (1917). (in German)
    55. Compton, A. (1923). "A quantum theory of the scattering of X-rays by light elements". Physical Review. 21 (5): 483–502. Bibcode:1923PhRv...21..483C. doi:10.1103/PhysRev.21.483.
    56. Pais, A. (1982). Subtle is the Lord: The science and the life of Albert Einstein. Oxford University Press. ISBN 978-0-19-853907-0.
    57. Millikan, R.A. (1924). "Robert A. Millikan's Nobel Lecture".
    58. Hendry, J. (1980). "The development of attitudes to the wave–particle duality of light and quantum theory, 1900–1920". Annals of Science. 37 (1): 59–79. doi:10.1080/00033798000200121.
    59. Bohr, N.; Kramers, H.A.; Slater, J.C. (1924). "The Quantum Theory of Radiation". Philosophical Magazine. 47 (281): 785–802. doi:10.1080/14786442408565262. Also Zeitschrift für Physik, 24, 69 (1924).
    60. Howard, Don (December 2004). "Who Invented the "Copenhagen Interpretation"? A Study in Mythology". Philosophy of Science. 71 (5): 669–682. doi:10.1086/425941. ISSN 0031-8248. JSTOR 10.1086/425941. S2CID 9454552.
    61. Heisenberg, W. (1933). "Heisenberg Nobel lecture".
    62. Mandel, L. (1976). E. Wolf (ed.). The case for and against semiclassical radiation theory. Progess in Optics. Progress in Optics. Vol. 13. North-Holland. pp. 27–69. Bibcode:1976PrOpt..13...27M. doi:10.1016/S0079-6638(08)70018-0. ISBN 978-0-444-10806-7.
    63. Grangier, P.; Roger, G.; Aspect, A. (1986). "Experimental evidence for a photon anticorrelation effect on a beam splitter: A new light on single-photon interferences". Europhysics Letters. 1 (4): 173–179. Bibcode:1986EL......1..173G. CiteSeerX 10.1.1.178.4356. doi:10.1209/0295-5075/1/4/004. S2CID 250837011.
    64. Thorn, J.J.; Neel, M.S.; Donato, V.W.; Bergreen, G.S.; Davies, R.E.; Beck, M. (2004). "Observing the quantum behavior of light in an undergraduate laboratory" (PDF). American Journal of Physics. 72 (9): 1210–1219. Bibcode:2004AmJPh..72.1210T. doi:10.1119/1.1737397.
    65. Taylor, G.I. (1909). Interference fringes with feeble light. Proceedings of the Cambridge Philosophical Society. Vol. 15. pp. 114–115.
    66. Saleh, B.E.A. & Teich, M.C. (2007). Fundamentals of Photonics. Wiley. ISBN 978-0-471-35832-9.
    67. Newton, T.D.; Wigner, E.P. (1949). "Localized states for elementary particles" (PDF). Reviews of Modern Physics. 21 (3): 400–406. Bibcode:1949RvMP...21..400N. doi:10.1103/RevModPhys.21.400.
    68. Bialynicki-Birula, I. (1994). "On the wave function of the photon". Acta Physica Polonica A. 86 (1–2): 97–116. Bibcode:1994AcPPA..86...97B. doi:10.12693/APhysPolA.86.97.
    69. Sipe, J.E. (1995). "Photon wave functions". Physical Review A. 52 (3): 1875–1883. Bibcode:1995PhRvA..52.1875S. doi:10.1103/PhysRevA.52.1875. PMID 9912446.
    70. Bialynicki-Birula, I. (1996). Photon wave function. Progess in Optics. Progress in Optics. Vol. 36. pp. 245–294. Bibcode:1996PrOpt..36..245B. doi:10.1016/S0079-6638(08)70316-0. ISBN 978-0-444-82530-8. S2CID 17695022.
    71. Scully, M.O.; Zubairy, M.S. (1997). Quantum Optics. Cambridge: Cambridge University Press. ISBN 978-0-521-43595-6.
    72. Busch, Paul; Lahti, Pekka; Werner, Reinhard F. (2013-10-17). "Proof of Heisenberg's Error-Disturbance Relation" (PDF). Physical Review Letters. 111 (16): 160405. arXiv:1306.1565. Bibcode:2013PhRvL.111p0405B. doi:10.1103/PhysRevLett.111.160405. ISSN 0031-9007. PMID 24182239. S2CID 24507489.
    73. Appleby, David Marcus (2016-05-06). "Quantum Errors and Disturbances: Response to Busch, Lahti and Werner". Entropy. 18 (5): 174. arXiv:1602.09002. Bibcode:2016Entrp..18..174A. doi:10.3390/e18050174.
    74. Landau, L.D.; Lifschitz, E.M. (1977). Quantum Mechanics: Non-Relativistic Theory. Vol. 3 (3rd ed.). Pergamon Press. ISBN 978-0-08-020940-1. OCLC 2284121.
    75. Busch, P.; Grabowski, M.; Lahti, P.J. (January 1995). "Who Is Afraid of POV Measures? Unified Approach to Quantum Phase Observables". Annals of Physics. 237 (1): 1–11. Bibcode:1995AnPhy.237....1B. doi:10.1006/aphy.1995.1001.
    76. Bose, S.N. (1924). "Plancks Gesetz und Lichtquantenhypothese". Zeitschrift für Physik (in German). 26 (1): 178–181. Bibcode:1924ZPhy...26..178B. doi:10.1007/BF01327326. S2CID 186235974.
    77. Einstein, A. (1924). "Quantentheorie des einatomigen idealen Gases". Sitzungsberichte der Preussischen Akademie der Wissenschaften (Berlin), Physikalisch-mathematische Klasse (in German). 1924: 261–267.
    78. Einstein, A. (1925). Quantentheorie des einatomigen idealen Gases, Zweite Abhandlung. Sitzungsberichte der Preussischen Akademie der Wissenschaften (Berlin), Physikalisch-mathematische Klasse (in German). Vol. 1925. pp. 3–14. doi:10.1002/3527608958.ch28. ISBN 978-3-527-60895-9.
    79. Anderson, M.H.; Ensher, J.R.; Matthews, M.R.; Wieman, C.E.; Cornell, E.A. (1995). "Observation of Bose–Einstein Condensation in a Dilute Atomic Vapor". Science. 269 (5221): 198–201. Bibcode:1995Sci...269..198A. doi:10.1126/science.269.5221.198. JSTOR 2888436. PMID 17789847.
    80. "Physicists Slow Speed of Light". News.harvard.edu (1999-02-18). Retrieved on 2015-05-11.
    81. "Light Changed to Matter, Then Stopped and Moved". photonics.com (February 2007). Retrieved on 2015-05-11.
    82. Streater, R.F.; Wightman, A.S. (1989). PCT, Spin and Statistics, and All That. Addison-Wesley. ISBN 978-0-201-09410-7.
    83. Einstein, A. (1916). "Strahlungs-emission und -absorption nach der Quantentheorie". Verhandlungen der Deutschen Physikalischen Gesellschaft (in German). 18: 318–323. Bibcode:1916DPhyG..18..318E.
    84. Section 1.4 in Wilson, J.; Hawkes, F.J.B. (1987). Lasers: Principles and Applications. New York: Prentice Hall. ISBN 978-0-13-523705-2.
    85. Einstein, A. (1916). "Strahlungs-emission und -absorption nach der Quantentheorie". Verhandlungen der Deutschen Physikalischen Gesellschaft (in German). 18: 318–323. Bibcode:1916DPhyG..18..318E. p. 322: Die Konstanten and würden sich direkt berechnen lassen, wenn wir im Besitz einer im Sinne der Quantenhypothese modifizierten Elektrodynamik und Mechanik wären."
    86. Dirac, P.A.M. (1926). "On the Theory of Quantum Mechanics". Proceedings of the Royal Society A. 112 (762): 661–677. Bibcode:1926RSPSA.112..661D. doi:10.1098/rspa.1926.0133.
    87. Dirac, P.A.M. (1927). "The Quantum Theory of the Emission and Absorption of Radiation". Proceedings of the Royal Society A. 114 (767): 243–265. Bibcode:1927RSPSA.114..243D. doi:10.1098/rspa.1927.0039.
    88. Dirac, P.A.M. (1927b). "The Quantum Theory of Dispersion". Proceedings of the Royal Society A. 114 (769): 710–728. Bibcode:1927RSPSA.114..710D. doi:10.1098/rspa.1927.0071.
    89. Heisenberg, W.; Pauli, W. (1929). "Zur Quantentheorie der Wellenfelder". Zeitschrift für Physik (in German). 56 (1–2): 1. Bibcode:1929ZPhy...56....1H. doi:10.1007/BF01340129. S2CID 121928597.
    90. Heisenberg, W.; Pauli, W. (1930). "Zur Quantentheorie der Wellenfelder". Zeitschrift für Physik (in German). 59 (3–4): 139. Bibcode:1930ZPhy...59..168H. doi:10.1007/BF01341423. S2CID 186219228.
    91. Fermi, E. (1932). "Quantum Theory of Radiation". Reviews of Modern Physics. 4 (1): 87. Bibcode:1932RvMP....4...87F. doi:10.1103/RevModPhys.4.87.
    92. Born, M. (1926). "Zur Quantenmechanik der Stossvorgänge". Zeitschrift für Physik (in German). 37 (12): 863–867. Bibcode:1926ZPhy...37..863B. doi:10.1007/BF01397477. S2CID 119896026.
    93. Born, M. (1926). "Quantenmechanik der Stossvorgänge". Zeitschrift für Physik (in German). 38 (11–12): 803. Bibcode:1926ZPhy...38..803B. doi:10.1007/BF01397184. S2CID 126244962.
    94. Pais, A. (1986). Inward Bound: Of Matter and Forces in the Physical World. Oxford University Press. p. 260. ISBN 978-0-19-851997-3. Specifically, Born claimed to have been inspired by Einstein's never-published attempts to develop a "ghost-field" theory, in which point-like photons are guided probabilistically by ghost fields that follow Maxwell's equations.
    95. Debye, P. (1910). "Der Wahrscheinlichkeitsbegriff in der Theorie der Strahlung". Annalen der Physik (in German). 33 (16): 1427–1434. Bibcode:1910AnP...338.1427D. doi:10.1002/andp.19103381617.
    96. Born, M.; Heisenberg, W.; Jordan, P. (1925). "Quantenmechanik II". Zeitschrift für Physik (in German). 35 (8–9): 557–615. Bibcode:1926ZPhy...35..557B. doi:10.1007/BF01379806. S2CID 186237037.
    97. Jaeger, Gregg (2019). "Are virtual particles less real?" (PDF). Entropy. 21 (2): 141. Bibcode:2019Entrp..21..141J. doi:10.3390/e21020141. PMC 7514619. PMID 33266857.
    98. Zee, Anthony (2003). Quantum Field Theory in a Nutshell. Princeton, N.J.: Princeton University Press. ISBN 0-691-01019-6. OCLC 50479292.
    99. Photon–photon-scattering section 7-3-1, renormalization chapter 8-2 in Itzykson, C.; Zuber, J.-B. (1980). Quantum Field Theory. McGraw-Hill. ISBN 978-0-07-032071-0.
    100. Weiglein, G. (2008). "Electroweak Physics at the ILC". Journal of Physics: Conference Series. 110 (4): 042033. arXiv:0711.3003. Bibcode:2008JPhCS.110d2033W. doi:10.1088/1742-6596/110/4/042033. S2CID 118517359.
    101. Ryder, L.H. (1996). Quantum field theory (2nd ed.). Cambridge University Press. ISBN 978-0-521-47814-4.
    102. Sheldon Glashow Nobel lecture, delivered 8 December 1979.
    103. Abdus Salam Nobel lecture, delivered 8 December 1979.
    104. Steven Weinberg Nobel lecture, delivered 8 December 1979.
    105. E.g., chapter 14 in Hughes, I.S. (1985). Elementary particles (2nd ed.). Cambridge University Press. ISBN 978-0-521-26092-3.
    106. Bauer, T.H.; Spital, R.D.; Yennie, D.R.; Pipkin, F.M. (1978). "The hadronic properties of the photon in high-energy interactions". Reviews of Modern Physics. 50 (2): 261. Bibcode:1978RvMP...50..261B. doi:10.1103/RevModPhys.50.261.
    107. Sakurai, J.J. (1960). "Theory of strong interactions". Annals of Physics. 11 (1): 1–48. Bibcode:1960AnPhy..11....1S. doi:10.1016/0003-4916(60)90126-3.
    108. Walsh, T.F.; Zerwas, P. (1973). "Two-photon processes in the parton model". Physics Letters B. 44 (2): 195. Bibcode:1973PhLB...44..195W. doi:10.1016/0370-2693(73)90520-0.
    109. Witten, E. (1977). "Anomalous cross section for photon–photon scattering in gauge theories". Nuclear Physics B. 120 (2): 189–202. Bibcode:1977NuPhB.120..189W. doi:10.1016/0550-3213(77)90038-4.
    110. Nisius, R. (2000). "The photon structure from deep inelastic electron–photon scattering". Physics Reports. 332 (4–6): 165–317. arXiv:hep-ex/9912049. Bibcode:2000PhR...332..165N. doi:10.1016/S0370-1573(99)00115-5. S2CID 119437227.
    111. E.g., section 10.1 in Dunlap, R.A. (2004). An Introduction to the Physics of Nuclei and Particles. Brooks/Cole. ISBN 978-0-534-39294-9.
    112. Radiative correction to electron mass section 7-1-2, anomalous magnetic moments section 7-2-1, Lamb shift section 7-3-2 and hyperfine splitting in positronium section 10-3 in Itzykson, C.; Zuber, J.-B. (1980). Quantum Field Theory. McGraw-Hill. ISBN 978-0-07-032071-0.
    113. E.g. sections 9.1 (gravitational contribution of photons) and 10.5 (influence of gravity on light) in Stephani, H.; Stewart, J. (1990). General Relativity: An Introduction to the Theory of Gravitational Field. Cambridge University Press. pp. 86 ff, 108 ff. ISBN 978-0-521-37941-0.
    114. Polaritons section 10.10.1, Raman and Brillouin scattering section 10.11.3 in Patterson, J.D.; Bailey, B.C. (2007). Solid-State Physics: Introduction to the Theory. Springer. ISBN 978-3-540-24115-7.
    115. Naeye, R. (1998). Through the Eyes of Hubble: Birth, Life and Violent Death of Stars. CRC Press. ISBN 978-0-7503-0484-9. OCLC 40180195.
    116. Koupelis, Theo; Kuhn, Karl F. (2007). In Quest of the Universe. Jones and Bartlett Canada. p. 102. ISBN 9780763743871.
    117. E.g. section 11-5 C in Pine, S.H.; Hendrickson, J.B.; Cram, D.J.; Hammond, G.S. (1980). Organic Chemistry (4th ed.). McGraw-Hill. ISBN 978-0-07-050115-7.
    118. Nobel lecture given by G. Wald on December 12, 1967, online at nobelprize.org: The Molecular Basis of Visual Excitation.
    119. Photomultiplier section 1.1.10, CCDs section 1.1.8, Geiger counters section 1.3.2.1 in Kitchin, C.R. (2008). Astrophysical Techniques. Boca Raton, FL: CRC Press. ISBN 978-1-4200-8243-2.
    120. Waymouth, John (1971). Electric Discharge Lamps. Cambridge, MA: The M.I.T. Press. ISBN 978-0-262-23048-3.
    121. Denk, W.; Svoboda, K. (1997). "Photon upmanship: Why multiphoton imaging is more than a gimmick". Neuron. 18 (3): 351–357. doi:10.1016/S0896-6273(00)81237-4. PMID 9115730. S2CID 2414593.
    122. Lakowicz, J.R. (2006). Principles of Fluorescence Spectroscopy. Springer. pp. 529 ff. ISBN 978-0-387-31278-1.
    123. Jennewein, T.; Achleitner, U.; Weihs, G.; Weinfurter, H.; Zeilinger, A. (2000). "A fast and compact quantum random number generator". Review of Scientific Instruments. 71 (4): 1675–1680. arXiv:quant-ph/9912118. Bibcode:2000RScI...71.1675J. doi:10.1063/1.1150518. S2CID 13118587.
    124. Stefanov, A.; Gisin, N.; Guinnard, O.; Guinnard, L.; Zbiden, H. (2000). "Optical quantum random number generator". Journal of Modern Optics. 47 (4): 595–598. doi:10.1080/095003400147908.
    125. Introductory-level material on the various sub-fields of quantum optics can be found in Fox, M. (2006). Quantum Optics: An introduction. Oxford University Press. ISBN 978-0-19-856673-1 – via Google Books.
    126. Hignett, Katherine (16 February 2018). "Physics creates new form of light that could drive the quantum computing revolution". Newsweek. Retrieved 17 February 2018.
    127. Liang, Qi-Yu; et al. (16 February 2018). "Observation of three-photon bound states in a quantum nonlinear medium". Science. 359 (6377): 783–786. arXiv:1709.01478. Bibcode:2018Sci...359..783L. doi:10.1126/science.aao7293. PMC 6467536. PMID 29449489.

    Further reading
    By date of publication
    Education with single photons
    • Quotations related to Photon at Wikiquote
    • The dictionary definition of photon at Wiktionary
    • Media related to Photon at Wikimedia Commons
    This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.