Ángulo beta (mecánica orbital)
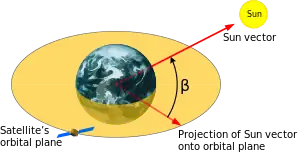
El ángulo beta (β) es una medida que se utiliza principalmente en los vuelos espaciales orbitales. El ángulo beta determina el porcentaje de tiempo que un satélite en órbita terrestre baja (LEO) pasa bajo la luz solar directa, absorbiendo energía solar.[1] El término se define como el ángulo entre el plano orbital del satélite y el vector hacia el Sol (es decir, la dirección desde la que brilla el Sol).[2] El ángulo beta es el menor de los dos ángulos entre el vector del Sol y el plano de la órbita del objeto. El ángulo beta no define un plano orbital único; todos los satélites en órbita con un ángulo beta dado a una altitud dada tienen la misma exposición al Sol, a pesar de que puedan estar orbitando en planos completamente diferentes alrededor de la Tierra.[3]
El ángulo beta varía entre +90° y −90°, y la dirección en la que el satélite orbita su cuerpo primario determina si el signo del ángulo beta es positivo o negativo. Un observador imaginario parado en el Sol define un ángulo beta como positivo si el satélite en cuestión orbita en sentido antihorario y negativo si gira en sentido horario.[3] La cantidad máxima de tiempo que un satélite en una misión LEO normal puede pasar a la sombra de la Tierra ocurre en un ángulo beta de 0°. Un satélite en esa órbita pasa al menos el 59% de su período orbital a la luz solar.[1][2]
Luz y sombra
El grado de sombreado orbital de un objeto en las experiencias LEO está determinado por el ángulo beta de ese objeto. Un objeto lanzado a una órbita inicial con una inclinación igual al complemento de la inclinación de la Tierra a la eclíptica resulta en un ángulo beta inicial de 0 grados (β = 0°) para el objeto en órbita. Esto permite que el objeto pase la mayor cantidad posible de su período orbital en la sombra de la Tierra, y resulta en una absorción extremadamente reducida de energía solar. En una LEO de 280 kilómetros, el objeto está expuesto a la luz solar a través del 59% de su órbita (aproximadamente 53 minutos a la luz del sol y 37 minutos a la sombra[2]). En el otro extremo, un objeto lanzado en una órbita paralela al terminador da como resultado un ángulo beta de 90 grados (β = 90°), y el objeto está expuesto a la luz solar el 100% del tiempo. Un ejemplo sería una órbita polar iniciada al amanecer o al anochecer local en un equinoccio. El ángulo beta se puede controlar para mantener un satélite lo más frío posible (para instrumentos que requieren bajas temperaturas, como cámaras infrarrojas) manteniendo el ángulo beta lo más cerca posible de cero o, por el contrario, para mantener un satélite lo más expuesto a la luz solar como sea posible (para la conversión de la luz solar por sus paneles solares, para la estabilidad solar de los sensores o para estudiar el Sol) manteniendo un ángulo beta lo más cercano posible a +90 o –90.
Determinación y aplicación de ángulos beta
El valor de un ángulo beta solar para un satélite en órbita terrestre se puede encontrar usando la ecuación
- ,
donde es la longitud solar eclíptica verdadera, es la longitud del nodo ascendente (LNA), es la inclinación de la órbita, y es la oblicuidad de la eclíptica (aproximadamente 23,45 grados para la Tierra en la actualidad). La LNA y la inclinación son propiedades de la órbita del satélite, y la longitud solar es una función de la posición de la Tierra en órbita alrededor del sol (aproximadamente linealmente proporcional al día del año en relación con el equinoccio vernal).[4]
La discusión anterior define el ángulo beta de los satélites que orbitan la Tierra, pero se puede calcular un ángulo beta para cualquier sistema de tres cuerpos en órbita: se puede aplicar la misma definición para dar el ángulo beta de otros objetos. Por ejemplo, el ángulo beta de un satélite en órbita alrededor de Marte, con respecto a la Tierra, define la cantidad de tiempo que el satélite tiene una línea de visión hacia la Tierra, es decir, determina cuánto tiempo brilla la Tierra en el satélite y cuánto tiempo la Tierra está bloqueada de la vista. Ese mismo satélite también tendrá un ángulo beta con respecto al Sol, y de hecho tiene un ángulo beta para cualquier objeto celeste para el que se desee calcular: cualquier satélite que orbita un cuerpo (es decir, la Tierra) estará en la sombra de ese cuerpo con respecto a un objeto celeste dado (como ser una estrella) algunas veces, y en su línea de visión el resto del tiempo. Los ángulos beta que describen órbitas no geocéntricas son importantes cuando las agencias espaciales lanzan satélites en órbitas alrededor de otros cuerpos en el Sistema Solar.
Importancia en vuelos espaciales
Cuando el transbordador espacial estaba en servicio en misiones a la Estación Espacial Internacional, el ángulo beta de la órbita de la misma era una consideración crucial; los períodos denominados «corte beta»,[1] durante los cuales el transbordador no pudo ser lanzado con seguridad a la ISS, fueron el resultado directo del ángulo beta de la estación espacial en esos momentos. Cuando el orbitador estaba en vuelo (no atracado en la ISS) y voló a un ángulo beta mayor a 60 grados, el orbitador entró en modo "asador" y giró lentamente alrededor de su eje X (eje de la nariz a la cola), por razones de regulación térmica. Para vuelos a la ISS, el transbordador podría lanzarse durante un corte beta de la ISS si la misma estuviese en una beta inferior a 60 grados en el muelle, y durante toda la fase de atraque.[5] Por lo tanto, la duración de la misión afectó el tiempo de lanzamiento cuando se acercaban las fechas de corte beta.
Referencias
- Derek Hassman, NASA Flight Director (1 de diciembre de 2002). «MCC Answers». NASA. Archivado desde el original el 24 de julio de 2020. Consultado el 14 de junio de 2009.
- «Earth's Thermal Environment». Thermal Environments JPL D-8160. K&K Associates. 2008. Consultado el 14 de julio de 2009.
- «Orbit Definition». Structural Dynamics Research Corporation. 2001. Consultado el 26 de agosto de 2009.
- Rickman, Steven. «Introduction to On-Orbit Thermal Environments Part III». NESC Academy. Consultado el 2 de noviembre de 2019.
- Hassman, Derek (2 de diciembre de 2012). «Mission Control Answers Your Questions». Archivado desde el original el 27 de febrero de 2003. Consultado el 2 de noviembre de 2019.