Árbol de decisión alternativo
Un Árbol de decisión alternativo es un método de clasificación proveniente del aprendizaje automático conocido en inglés como Alternating Decision Tree (ADTree).
Las estructuras de datos y los algoritmos son una generalización de los árboles de decisión. El ADTree fue introducido por Yoav Freund y Llew Mason en 1999.
Un ADTree consiste en una alternancia de nodos de decisión, que especifican una condición determinante, y predicción, que contienen un solo número.
Una instancia es clasificada por un ADTree siguiendo todos los caminos para que todos los nodos de decisión sean verdaderos, y suma algún nodo de predicción que es recorrida.
Historia
ADTrees fueron introducidos por Yoav Freund y Llew Mason. sin embargo, el algoritmo presentado tenía varios errores tipográficos. Aclaraciones y optimizaciones que fueron presentadas más tarde por Bernhard Pfahringer, Geoffrey Holmes y Richard Kirkby. Las implementaciones están disponibles en Weka y JBoost.
Motivación
Los algoritmos de impulso originales usan típicamente los tocones de decisión o los árboles de decisión como hipótesis débiles. Por ejemplo, el impulso de los tocos de decisión crea un conjunto de T, (donde T es el número de iteraciones de refuerzo), que luego votan sobre la clasificación final de acuerdo con sus pesos. Los tocones individuales de decisión se ponderan según su capacidad de clasificar los datos.
Impulsar un alumno simple resulta en un conjunto no estructurado de T hipótesis, lo que hace difícil inferir las correlaciones entre los atributos. Los árboles alternos de decisión introducen la estructura al conjunto de hipótesis al requerir que construyan una hipótesis que se produjo en una iteración anterior. El conjunto resultante de hipótesis se puede visualizar en un árbol basado en la relación entre una hipótesis y su "padre".
Otra característica importante de los algoritmos potenciados es que los datos reciben una distribución diferente en cada iteración. Las instancias que se clasifican erróneamente se dan un peso más grande mientras que las instancias exactamente clasificadas se dan el peso reducido.
Estructura de árbol de decisión alternativa
Un árbol de decisiones alternativo consta de nodos de decisión y nodos de predicción. Los nodos de decisión especifican una condición de predicado. Los nodos de predicción contienen un solo número. ADTrees siempre tienen nodos de predicción tanto como raíz y hojas. Una instancia es clasificada por un ADTree siguiendo todas las rutas para las cuales todos los nodos de decisión son verdaderos y sumando cualquier nodo de predicción que se atraviesa. Esto es diferente de árboles de clasificación binaria como CART (árbol de clasificación y regresión) o C4.5 en el que una instancia sigue solo un camino a través del árbol.
Ejemplo
El siguiente árbol fue construido usando JBoost en el conjunto de datos spambase (disponible en el UCI Machine Learning Repository). En este ejemplo, el spam se codifica como 1 y el correo electrónico regular se codifica como -1
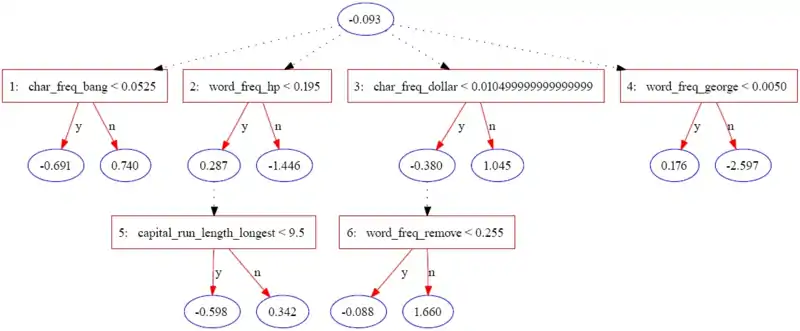
La siguiente tabla contiene parte de la información de una única instancia.
Una instancia a clasificar.
| Feature | Value |
|---|---|
| char_freq_bang | 0.08 |
| word_freq_hp | 0.4 |
| capital_run_length_longest | 4 |
| char_freq_dollar | 0 |
| word_freq_remove | 0.9 |
| word_freq_george | 0 |
| Other features | ... |
Puntuación para la instancia anterior.
| Iteration | 0 | 1 | 2 | 3 | 4 | 5 | 6 |
|---|---|---|---|---|---|---|---|
| Instance values | N/A | .08 < .052 = f | .4 < .195 = f | 0 < .01 = t | 0 < 0.005 = t | N/A | .9 < .225 = f |
| Prediction | -0.093 | 0.74 | -1.446 | -0.38 | 0.176 | 0 | 1.66 |
La puntuación final de 0.657 es positiva, por lo que la instancia se clasifica como spam. La magnitud del valor es una medida de confianza en la predicción. Los autores originales enumeran tres niveles potenciales de interpretación para el conjunto de atributos identificados por un ADTree:
- Los nodos individuales pueden ser evaluados para su propia capacidad predictiva.
- Los conjuntos de nodos en la misma trayectoria pueden ser interpretados como teniendo un efecto común
- El árbol puede ser interpretado como un todo.
Se debe tener cuidado al interpretar nodos individuales ya que las puntuaciones reflejan una nueva ponderación de los datos en cada iteración.
Descripción del algoritmo
Las entradas del algoritmo de árbol de decisiones alternativo son:
- Un conjunto de entradas (x 1, y1), ..., (xm, ym) donde xi es un vector de atributos yi -1 O 1. Las entradas también se llaman instancias.
- Un conjunto de pesos wi que corresponde a cada instancia.
El elemento fundamental del algoritmo ADTree es la regla. Una sola regla consiste en una precondición, una condición y dos puntajes. Una condición es un predicado de la forma "atributo <comparación> valor". Una precondición es simplemente una conjunción lógica de condiciones. La evaluación de una regla implica un par de sentencias if anidadas:
- if(precondition)
- if(condition)
- return score_one
- else
- return score_two
- end if
- else
- return 0
- end if
El algoritmo también requiere varias funciones auxiliares:
- W + ( c ) devuelve la suma de los pesos de todos los ejemplos marcados positivamente que satisfacen el predicado c.
- W − ( c ) devuelve la suma de los pesos de todos los ejemplos marcados negativamente que satisfacen el predicado c.
- W ( c ) = W + ( c ) + W − ( c ) devuelve la suma de los pesos de todos los ejemplos que satisfacen el predicado c.
El algoritmo es como sigue:
1 function ad_tree
2 input Set of m training instances
4 wi = 1/m for all i
5
6 R0 = a rule with scores a and 0, precondition "true" and condition "true."
7
8 the set of all possible conditions
9 for
10 get values that minimize
11
12
13
14 Rj = new rule with precondition p, condition c, and weights a1 and a2
15
16 end for
17 return set of Rj
El conjunto P crece por dos precondiciones en cada iteración, y es posible derivar la estructura de un conjunto de reglas tomando nota de la precondición que Se utiliza en cada regla sucesiva.
Resultados empíricos
La Figura 6 del documento original demuestra que los ADTrees suelen ser tan robustos como los árboles de decisión potenciados y los tocos de decisión potenciados. Normalmente, se puede lograr una exactitud equivalente con una estructura de árbol mucho más simple que los algoritmos de partición recursiva.
Referencias
- Yoav Freund and Llew Mason. The Alternating Decision Tree Algorithm. Proceedings of the 16th International Conference on Machine Learning, pages 124-133 (1999)
- Jump up^ Bernhard Pfahringer, Geoffrey Holmes and Richard Kirkby. Optimizing the Induction of Alternating Decision Trees. Proceedings of the Fifth Pacific-Asia Conference on Advances in Knowledge Discovery and Data Mining. 2001, pp. 477-487
- Jump up^
- Jump up^ "UCI Machine Learning Repository". Ics.uci.edu. Retrieved 2012-03-16.
Enlaces externos
- An introduction to Boosting and ADTrees (Has many graphical examples of alternating decision trees in practice).
- JBoost software implementing ADTrees.
- http://perun.pmf.uns.ac.rs/radovanovic/dmsem/cd/install/Weka/doc/classifiers-papers/trees/ADTree/atrees.pdf