Átomo de Rydberg

Un átomo de Rydberg es un átomo excitado con uno o varios electrones en estados con un número cuántico principal alto.[1][2] Estos átomos tienen propiedades bastante particulares, entre las que se encuentran una respuesta exagerada a campos eléctricos y magnéticos,[3] tiempos de decaimiento largos y funciones de onda electrónicas que se aproximan (bajo ciertas condiciones) a las órbitas clásicas de los electrones alrededor del núcleo.[4] Estos electrones externos perciben un potencial similar al potencial eléctrico dado por un átomo de hidrógeno, pues los electrones internos apantallan a los electrones de valencia del campo eléctrico creado por el núcleo.[5]

Niveles de energía en el átomo de Litio que muestra la serie de Rydberg de los 3 valores más bajos de momento angular orbital que convergen en la primera energía de ionización.

A pesar de sus deficiencias, el modelo atómico de Bohr es útil para explicar estas propiedades. Desde el punto de vista clásico, un electrón en una órbita circular de radio r alrededor de un núcleo de hidrógeno de carga +e, obedece la segunda ley de Newton:

${\displaystyle \mathbf {F} =m\mathbf {a} \Rightarrow {ke^{2} \over r^{2}}={mv^{2} \over r}}$

donde k = 1/(4πε₀).

El momento orbital se encuentra cuantizado en unidades de ħ:

${\displaystyle mvr=n\hbar }$

Combinando estas dos ecuaciones llegamos a la expresión de Bohr para el radio orbital en función del número principal cuántico, n:

${\displaystyle r={n^{2}\hbar ^{2} \over ke^{2}m}.}$

Partiendo de esta ecuación uno puede comprender por qué los átomos de Rydberg muestran propiedades tan particulares: el radio orbital escala como n² (el estado con n = 137 de hidrógeno tiene un radio orbital ~1 µm), y la sección efectiva geométrica crece como n⁴. Así pues, los átomos de Rydberg son extremadamente grandes y sus electrones de valencia, ligados débilmente al núcleo, son perturbados fácilmente o incluso ionizados por colisiones o campos externos.

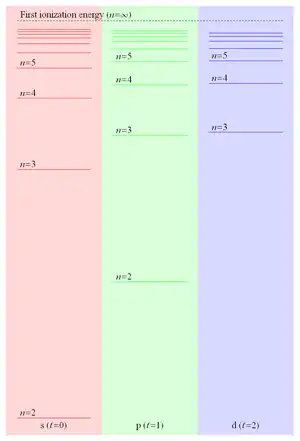
Dado que la energía de ligadura de un electrón en un estado de Rydberg es proporcional a 1/r, y por lo tanto disminuye como 1/n², el espaciado energético entre niveles adyacentes disminuye como 1/n³, lo que da lugar a niveles cada vez más cercanos que convergen a la primera energía de ionización. Estos estados tan cercanos forman lo que se conoce como la serie de Rydberg.