Adición matricial
En matemáticas, la adición matricial es la operación de sumar dos matrices sumando las componentes o elementos correspondientes. Sin embargo, hay otras operaciones que también podrían considerarse tipos de adición para matrices, la suma directa y el producto de Kronecker.
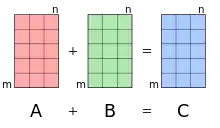
Suma por componentes
Dos matrices tienen que tener un número igual de filas y columnas para poder sumarlas.[1] La suma de dos matrices A y B es una matriz que tiene el mismo número de filas y columnas que A y B. La suma de A y B, denotada como A + B, se computa añadiendo los elementos correspondientes de A y B:[2][3]
Por ejemplo:
También podemos substraer una matriz de otra, siempre que tengan las mismas dimensiones. A − B se computa restando los elementos correspondientes de A y B, y tiene las mismas dimensiones de A y B. Por ejemplo:
Suma directa
Otra operación, menos utilizada, es la suma directa (denotada por ⊕). Notar que la suma Kronecker se denota también por ⊕; el contexto tendría que hacer el uso claro. La suma directa de cualquier par de matrices A de dimensiones m × n y B de dimensiones p × q es una matriz de dimensiones (m + p) × (n + q) definida como[4][2]
Por ejemplo,
La suma directa de matrices es un tipo especial de matriz de bloque, en particular la suma directa de matrices cuadradas es un bloque matriz diagonal.
La matriz de adyacencia de la unión de grafos disjuntos o multigrafos es la suma directa de sus matrices de adyacencia. Cualquier elemento en la suma directa de dos espacios vectoriales de matrices pueden ser representados como suma directa de dos matrices.
En general, la suma directa de n matrices es:[2]
donde los ceros son de hecho bloques de ceros, i.e. cero matrices.
Suma Kronecker
La suma Kronecker es diferente de la suma directa pero es también denotada por ⊕. Se define utilizando el producto Kronecker ⊗ y adición matricial normal. Si A es de tamaño n-por-n, B de tamaño m-por-m y denota la matriz identidad de k-por-k entonces la suma Kronecker está definida por:
Véase también
Referencias
- Elementary Linear Algebra by Rorres Anton 10e p53
- Lipschutz , Lipson.
- Riley, K.F.; Hobson, M.P.; Bence, S.J. (2010). Mathematical methods for physics and engineering. Cambridge University Press. ISBN 978-0-521-86153-3.
- Weisstein, Eric W. «Matrix Direct Sum». En Weisstein, Eric W, ed. MathWorld (en inglés). Wolfram Research.
Bibliografía utilizada
- Lipschutz, S.; Lipson, M. (2009). Lipschutz, S.; Lipson, M. (2009). Linear Algebra. ISBN 978-0-07-154352-1.