Algoritmo de Marzullo

Marzullo es eficaz en plazos de tiempo para producir un valor óptimo de un conjunto de estimaciones con intervalos desfasados donde el valor real puede estar fuera del intervalo de confianza para algunas fuentes. En este caso la estimación mejor está tomada para ser el intervalo más pequeño compatible con el número más grande de fuentes.

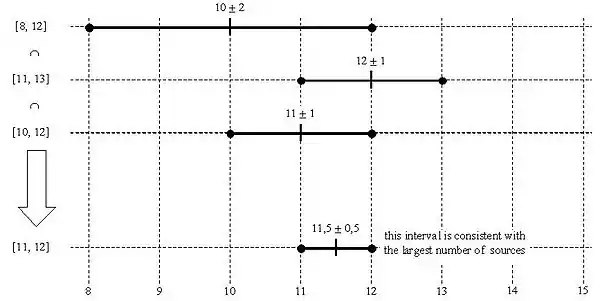
Si tenemos las estimaciones 10 ± 2, 12 ± 1 y 11 ± 1, entonces estos intervalos son [8,12], [11,13] y [10,12] los que cruzan para formar [11,12] o 11.5 ± 0.5 cuando compatible con todo tres valores.

Marzullo algoritmo, ejemplo#1

Si en cambio los rangos son [8,12], [11,13] y [14,15] entonces no hay ningún intervalo compatible con todos estos valores pero [11,12] es compatible con el número más grande de fuentes — concretamente, dos de ellos.

Finalmente, si los rangos son [8,9], [8,12] y [10,12] entonces ambos intervalos [8,9] y [10,12] son compatible con el número más grande de fuentes.

Este procedimiento determina un intervalo. Si el resultado deseado es un valor mejor de aquel intervalo entonces una aproximación sería tomar el centro del intervalo como el valor, que estuvo especificado en el original algoritmo de Marzullo. Una aproximación más sofisticada reconocería que esto podría dejar fuera información útil de los intervalos de confianza de las fuentes y que un modelo probabilista de las fuentes podría devolver otro valor, distinto al centro.

Nota que el valor computado es probablemente mejor descrito como "optimista" más que "optimal". Por ejemplo, considera tres intervalos [10,12], [11, 13] y [11.99,13]. El algoritmo descrito abajo computa [11.99, 12] o 11.995 ± 0.005 cuál es un valor muy preciso . Si sospechamos que uno de las estimaciones podría ser incorrecta, entonces al menos dos de las estimaciones tienen que ser correctas. Bajo esta condición, la estimación mejor es [11,13] desde este es el intervalo más grande que siempre cruza al menos dos estimaciones. El algoritmo descrito abajo es fácilmente parametrizable con el número máximo de estimaciones incorrectas.

El algoritmo de Marzullo empieza preparando una tabla de las fuentes, ordenándola y entonces buscando (de forma eficiente) las intersecciones de intervalos. Para cada fuente es un rango [c−r,c+r] definido por c ± r. Para cada rango la tabla tendrá dos tuplas de la forma <offset, type>. Una tupla representará el principio del rango, marcado con tipo −1 cuando <c−r,−1> y el otro representará el fin con tipo +1 cuando <c+r,+1>.

La descripción del algoritmo utiliza las variables siguientes: best (número más grande de overlapping los intervalos encontrados), cnt (número actual de intervalos overlapping), beststart y bestend (el principio y fin del intervalo mejor encontrado tan lejano), i (un índice), y la tabla de tuplas.

1. Construir la tabla de tuplas.
2. Ordena la taba por el offset. (Si existen dos tuplas con el mismo offset pero de tipos opuestos, indica que los intervalos son contiguos, un intervalo acaba tan otro empieza, entonces se necesita un método para decidir cuál va primero. Tal una ocurrencia puede ser considerada un overlap sin duración, los cuales pueden ser encontrados por el algoritmo por poner tipo −1 antes de que tipo +1. Si tal patológico overlaps está considerado objectionable pueden ser evitados por poner tipo +1 antes de que −1 en este caso.)
3. [Inicializa] best=0 cnt=0
4. [Bucle] pasa por cada tupla en la tabla en orden ascendente

1. [Número actual de overlapping intervalos] cnt=cnt−tipo[i]
2. Si cnt>best entonces best=cnt beststart=offset[i] bestend=offset[i+1]

Comentario: la próxima tupla, en [i+1], tampoco será fin de un intervalo (tipo=+1) en este caso finaliza el mejor intervalo, o será un principio de un intervalo (tipo=−1) y en el paso próximo reemplazará best.

Ambigüedad: no especifica que hacer si best=cnt. Esto es una condición de un lazo para overlap más grande. Tampoco se puede decidir tomar el más pequeño de bestend−beststart u offset[i+1]−offset[i] o justo tomar un arbitrario de las dos entradas igualmente buenas.

1. [Bucle de fin] regreso [beststart, bestend] como optimal intervalo. El número de fuentes falsas (devuelve las que no tienen overlap con el intervalo optimal) es el número de fuentes menos el valor de best.

El algoritmo de Marzullo es eficaz en espacio y tiempo. El uso espacial asintótico es O(n), donde n es el número de fuentes. Teniendo en cuenta el requisito de tiempo asintótico el algoritmo puede considerar construir la tabla, ordenándolo y buscándolo. El orden puede ser hecho en O(n log n) tiempo, y esto domina el armado y la búsqueda se realiza por etapas que se van mejorando en tiempo lineal. Por tanto, la eficacia de tiempo del algoritmo de Marzullo, es O(n log n).

Cuando la tabla está construida y ordenada es posible actualizar el intervalo para una fuente (cuando la información nueva está recibida) en tiempo lineal. Por tanto, actualizar datos para una fuente y encontrar el mejor intervalo puede ser hecho en O(n) tiempo.

• K. Un. Marzullo. Manteniendo el Tiempo en un Sistema Distribuido: Un Ejemplo de un Loosely-Coupled Servicio Distribuido. Ph.D. Disertación, Stanford Universidad, Departamento de Ingeniería Eléctrica, febrero de 1984.

• David L. Mills, Una Historia Breve de Tiempo NTP: Confesiones de un Internet Timekeeper
• Página web de Keith Marzullo