Análisis formal de conceptos

Cada uno de los grupos de objetos determinados por sus características comunes se define como un Begriffsumfang (extensión del concepto) y el conjunto correspondiente de todas las características comunes como un Begriffsinhalt (intensión). Ambas partes en conjunto, es decir, respectivamente, cada extensión con su correspondiente intensión, conforman un «concepto formal», donde la adenda «formal» indica que se trata de una construcción matemática. Un concepto formal está siempre determinado de manera unívoca tanto por su extensión como por su intensión.

Un concepto formal es un hipónimo (concepto subordinado) de un segundo concepto formal cuando su extensión está contenida de manera completa dentro de la extensión del segundo. Por tanto, la intensión del hiperónimo (del concepto con la extensión mayor) está contenida en la intensión del concepto hipónimo.[Nota 2]

Este tipo de orden de los conceptos formales hipónimo-hiperónimo se manifiesta por regla general como una estructura ordenada en forma de malla con ramificaciones, comúnmente no tiene forma de forma de árbol y ni menos es lineal. Se puede demostrar, sin embargo, que estos órdenes poseen características especiales y bien estudiadas: se trata aquí de los retículos completos.[Nota 3]

De esta manera, un concepto puede tener no solo un único concepto superordinado (hiperónimo). Más bien, la regla es que para cada concepto sean varios sus hiperónimos, también aquellos que no están en relación entre sí a nivel del concepto superordinado. Por ejemplo, el concepto ave rapaz (o cazadora) reúne las características tanto de su concepto hiperónimo, aves, como también las de otro concepto hiperónimo, animales cazadores.

La teoría en su actual formulación se remonta al grupo de investigación de Darmstadt del círculo de Rudolf Wille, Bernhard Ganter y Peter Burmeister donde surgió a comienzos de los años 1980 el análisis formal de conceptos. Los fundamentos matemáticos, sin embargo, fueron desarrollados en los años 1930 en el contexto de la teoría general de retículos. Antes de los trabajos del grupo de Darmstadt ya existían algunas aproximaciones de distintos grupos franceses. Los escritos de Charles S. Peirce y Hartmut von Hentig también tuvieron influencia en el surgimiento del análisis formal de conceptos.

El AFC tiene aplicación práctica en varias áreas, tales como la minería de datos y la minería de textos, la Gestión del conocimiento, web semántica, ingeniería de software, economía y biología.

Dados dos conjuntos ${\displaystyle G,\,M}$ y una relación ${\displaystyle I\subseteq G\times M}$. Entonces, el trío ${\displaystyle \mathbb {K} =(G,M,I)}$ se denomina contexto formal,[5] ${\displaystyle G}$ conjunto de objetos y ${\displaystyle M}$ su conjunto de características; para un objeto ${\displaystyle g\in G}$ y una característica ${\displaystyle m\in M}$ significa ${\displaystyle (g,m)\in I}$ «el objeto ${\displaystyle g}$ tiene la característica ${\displaystyle m}$“. Frecuentemente se escribe también como ${\displaystyle g{\mathrel {I}}m}$ en vez de ${\displaystyle (g,m)\in I}$. El conjunto ${\displaystyle I}$ se denomina relación de incidencia del contexto formal.

Si los conjuntos ${\displaystyle G}$ y ${\displaystyle M}$ son finitos, entonces pueden los contextos formales representarse bien como «tablas cruzadas». Tómese en cuenta aquí que objetos y características pueden ordenarse de manera arbitraria en esta representación. Pero ese orden, entonces, no forma parte del contexto formal, sino solo de su representación.

Un contexto formal acerca de las características de los números de 1 a 10.

Sea ${\displaystyle A\subseteq G}$ un conjunto de objetos de un contexto formal ${\displaystyle \mathbb {K} =(G,M,I)}$, entonces se denota con

${\displaystyle A':=\{\,m\in M\mid \forall g\in A:g{\mathrel {I}}m\,\}}$

el conjunto de las características comunes de los objetos en ${\displaystyle A}$. Respectivamente, se define para un conjunto ${\displaystyle B\subseteq M}$ de características de ${\displaystyle \mathbb {K} =(G,M,I)}$ el conjunto

${\displaystyle B':=\{\,g\in G\mid \forall m\in B:g{\mathrel {I}}m\,\}}$

de todos los objetos que poseen todas las características de ${\displaystyle B}$. Los conjuntos ${\displaystyle A'}$ y ${\displaystyle B'}$ se denominan «derivaciones» (Ableitungen/derivative) de los correspondientes conjuntos ${\displaystyle A}$ y ${\displaystyle B}$ y las funciones, designadas ambas con ${\displaystyle (\cdot )'}$ , se denominan «operadores de derivación» ${\displaystyle \mathbb {K} }$.

Los operadores de derivación cumplen con una serie de propiedades fundamentales. Sean ${\displaystyle A,\,A_{1},\,A_{2}}$ conjuntos de objetos y ${\displaystyle B,\,B_{1},\,B_{2}}$ conjuntos de características, entonces:

• ${\displaystyle A_{1}\subseteq A_{2}\,\implies \,A_{2}'\subseteq A_{1}'}$ y dual ${\displaystyle B_{1}\subseteq B_{2}\,\implies \,B_{2}'\subseteq B_{1}'}$,
• ${\displaystyle A\subseteq A''}$ y dual ${\displaystyle B\subseteq B''}$,
• ${\displaystyle A'=A'''}$ y ${\displaystyle B'=B'''}$,
• ${\displaystyle A\subseteq B'\iff A'\supseteq B}$.

En realidad, con esto los operadores de derivación definen una conexión de Galois antítona entre los retículos de conjuntos potencia de los conjuntos de objetos y los conjuntos de características. A la inversa, cualquiera de estas conexiones de Galois entre retículos de conjuntos potencia puede representarse como un par de operadores de derivación de un contexto formal.

Para un contexto formal ${\displaystyle \mathbb {K} }$ un par ${\displaystyle (A,B)}$ se denomina entonces un concepto formal[5] de ${\displaystyle \mathbb {K} }$, si se cumple:

• ${\displaystyle A}$ es un conjunto de objetos de ${\displaystyle \mathbb {K} }$,
• ${\displaystyle B}$ es un conjunto de características de ${\displaystyle \mathbb {K} }$,
• ${\displaystyle A'=B}$ y
• ${\displaystyle B'=A}$.

El conjunto ${\displaystyle A}$ se denomina entonces extensión y el conjunto ${\displaystyle B}$ intensión (contenido) del concepto ${\displaystyle (A,B)}$ . El conjunto de todos los conceptos se designa con ${\displaystyle {\mathfrak {B}}(\mathbb {K} )}$. Si se representan los contextos formales como tablas cruzadas, se pueden comprender los conceptos formales — existiendo un orden apropiado de los objetos y características — como rectángulos máximos completamente llenos en esa tabla cruzada.

Finalmente, sean ${\displaystyle (A,B),(C,D)\in {\mathfrak {B}}(\mathbb {K} )}$, entonces con

${\displaystyle (A,B)\leq (C,D)\,\Leftrightarrow \,A\subseteq C}$

se puede definir un orden parcial ${\displaystyle {\mathfrak {B}}(\mathbb {K} )}$. Ese orden constituye entonces la estructura ${\displaystyle ({\mathfrak {B}}(\mathbb {K} ),\leq )}$ en un retículo completo. De hecho, a la inversa, según el teorema principal del análisis formal de conceptos, todo retículo completo es isomorfo respecto de un retículo de conceptos.

Retículo de conceptos para el contexto numérico dado

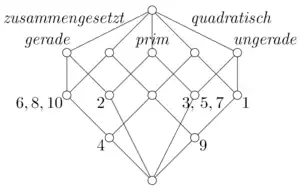
Los retículos de conceptos pueden representarse como diagramas de orden (diagramas de líneas) y desplegar así los datos en su estructura y sus relaciones. En ellos, todos los objetos tienen características (unidas por los cantos); en el ejemplo que figura al lado es 4 un número par, compuesto, cuadrado.

De manera matemáticamente más precisa se puede fundamentar primeramente la rotulación simplificada de retículos de conceptos. Si se considera para un objeto ${\displaystyle g\in G}$ el conjunto de todos los conceptos que contienen ${\displaystyle g}$ en su extensión, entonces ese conjunto tiene un filtro principal en el retículo de conceptos. Por eso el objeto ${\displaystyle g}$ se registra solo debajo del concepto más pequeño, que contiene ${\displaystyle g}$ en la extensión. Dualmente, se registra la característica ${\displaystyle m}$ encima del concepto más grande que posee una característica dada ${\displaystyle m\in M}$ en la intensión (contenido). En el diagrama de orden, un concepto tiene entonces exactamente un objeto en su extensión cuando se encuentra por encima del concepto que está rotulado con el objeto. Correspondientemente, un concepto tiene, en el diagrama de orden, una característica en su intensión (contenido) cuando está por debajo del concepto que está rotulado con esa característica.

Sea ${\displaystyle \mathbb {K} =(G,M,I)}$ un contexto formal y ${\displaystyle {\underline {\mathfrak {B}}}(\mathbb {K} )}$ su retículo de conceptos. Se pueden considerar para objetos ${\displaystyle g\in G}$ y características ${\displaystyle m\in M}$ los conceptos

${\displaystyle \gamma (g)=(\{\,g\,\}'',\{\,g\,\}'),}$

${\displaystyle \mu (m)=(\{\,m\,\}',\{\,m\,\}'')}$

Se denomina ${\displaystyle \gamma (g)}$ al concepto de objeto de ${\displaystyle g}$ y ${\displaystyle \mu (m)}$ al concepto de característica de ${\displaystyle m}$. Además rige

${\displaystyle g{\mathrel {I}}m\iff \gamma (g)\leq \mu (m)}$

Sea, por último, ${\displaystyle {\underline {L}}=(L,\leq _{L})}$ un retículo completo, entonces ${\displaystyle {\underline {L}}}$ entonces es isomorfo respecto de ${\displaystyle {\underline {\mathfrak {B}}}(\mathbb {K} )}$, precisamente cuando existen aplicaciones ${\displaystyle \gamma _{\underline {L}}\colon G\to L,\mu _{\underline {L}}\colon M\to L}$ tales que rige

${\displaystyle g{\mathrel {I}}m\iff \gamma _{\underline {L}}(g)\leq \mu _{\underline {L}}(m)}$

En particular, ${\displaystyle {\underline {L}}}$ es isomorfo respecto de ${\displaystyle {\underline {\mathfrak {B}}}(L,L,\leq _{L})}$.

Es posible representar con ayuda de un contexto formal la teoría de implicaciones de un área temática determinada. En particular, esto significa que uno puede hacerlo con ayuda de un conjunto suficiente de ejemplos que se transformen en los objetos del contexto formal. En teoría, un conjunto tal de ejemplos podría ser aportado por un experto humano o también por una máquina.

Aquí surge, sin embargo, el problema de que ni está garantizado de partida que esté dado una conjunto suficiente de ejemplos, ni que no sean redundantes algunos de los ejemplos generados, debido a que los ejemplos ya dados alcancen. Considerando que la generación de buenos ejemplos resulta difícil, las entrevistas a expertos o hasta la realización de nuevos experimentos son iniciativas caras, al tiempo que la investigación bibliográfica o de algoritmos puede ser costosa, se trata de un problema serio.

Aquí puede ser útil el algoritmo de la exploración de características. A partir de un conjunto previamente conocido de implicaciones y un conjunto ya conocido de ejemplos de esa área temática, el algoritmo propone implicaciones que luego pueden ser aceptadas o rechazadas por un experto (humano o no). Aquí una implicación debe ser aceptada exactamente cuando ella es válida en dicha área temática. Si una implicación se rechaza, el experto tiene que crear un contraejemplo que luego puede ser aceptado o rechazado por un experto (humano o no). A través de un contraejemplo aceptado, la implicación se refuta y con ello genera un conjunto lo más pequeño posible de implicaciones aceptadas que finalmente describe completamente el área temática. Más allá de ello, también se completa el conjunto de los ejemplos.