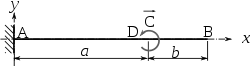Anexo:Pendientes y deformaciones en vigas
En este artículo se muestran las fórmulas que se aplican para calcular pendientes y deformaciones en vigas, o sea la flecha máxima y el giro en el apoyo para algunos casos particulares de la curva elástica que se produce en vigas sometidas a cargas.
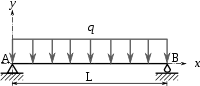
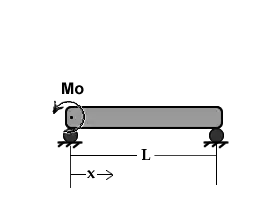
Vigas con soportes simples (biapoyadas)
En las siguientes fórmulas E designa al módulo de Young del material en que está construida la viga, e I al segundo momento de área de la sección transversal de la misma y L la luz de la viga:
| Tipo de carga | Pendiente | Deformación | Curva elástica | ||
|---|---|---|---|---|---|
|
para |
||||
|
para |
||||
|
|||||
|
para |
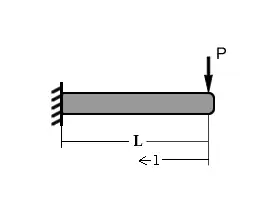
Vigas en voladizo (ménsulas empotradas)
| Tipo de carga | Pendiente | Deformación | Curva elástica | ||
|---|---|---|---|---|---|
|
|||||
|
cuando : cuando : | ||||
|
|||||
|
|
||||
|
|||||
|
|||||
Vigas biempotradas
Las vigas biempotradas son casos de vigas hiperestáticas que requieren la determinación de los momentos de empotramiento, antes de poder calcular directamente las pendientes y los desplazamientos sobre las mismas.
| Tipo de carga | Reacciones | Pendiente, desplazamiento máximo y curva elástica | ||
|---|---|---|---|---|
|
|
| ||
|
|
Véase también
Enlaces externos
Este artículo ha sido escrito por Wikipedia. El texto está disponible bajo la licencia Creative Commons - Atribución - CompartirIgual. Pueden aplicarse cláusulas adicionales a los archivos multimedia.