Anticadena

En matemáticas, una anticadena en un conjunto parcialmente ordenado A es un subconjunto S de A tal que cada par de miembros de S es incomparable, es decir, para cualquier x, y en S, ni x ≤ y ni y ≤ x.

El número de anticadenas no vacías definidas sobre un conjunto A dado se conoce como número de Dedekind.

El teorema de Dilworth establece que la no existencia de una anticadena de tamaño n+1 en S es una condición necesaria y suficiente para que S sea la unión de n órdenes totales o cadenas. Esto motiva preguntas sobre el tamaño de la anticadena máxima.

Por ejemplo, en el conjunto de partes de un conjunto finito X, ordenado por la inclusión, una anticadena máxima es descrita por el lema de Sperner, como los subconjuntos de tamaño 'mediano',|X|/2 en caso de que |X| sea par, y, o bien de (|X|+1)/2 o bien (|X|-1)/2 cuando |X| sea impar; la cardinalidad es el relevante coeficiente binomial.

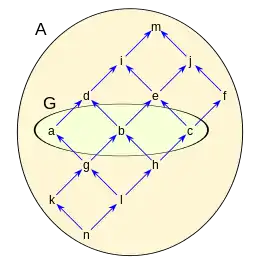
En la figura dado el conjunto A formado por los elementos:

${\displaystyle A=\{a,b,c,d,e,f,g,h,i,k,l,m,n\}}$

en el que se ha definido una relación binaria ${\displaystyle \precsim }$, siendo ${\displaystyle (A,\precsim )}$ un conjunto parcialmente ordenado.

dado el subconjunto G de A:

${\displaystyle G=\{a,b,c\}}$

Se puede ver que G es una anticadena dado que sus elemento son no comparables.