Aprendizaje automático cuántico
El aprendizaje automático cuántico (en inglés Quantum machine learning) es una novedosa área de investigación interdisciplinar, situada entre la mecánica cuántica y la informática, que suma esfuerzos para combinar la mecánica cuántica y el aprendizaje automático.[1][2] Los algoritmos o modelos de aprendizaje automático cuántico intentan usar las ventajas de la información cuántica con el fin de mejorar el aprendizaje automático clásico, por ejemplo desarrollando implementaciones eficientes de pesados algoritmos clásicos mediante computación cuántica.[3][4] Además, el aprendizaje automático cuántico incluye también la aproximación recíproca, aplicando los métodos de aprendizaje automático clásico a la teoría de la información cuántica.
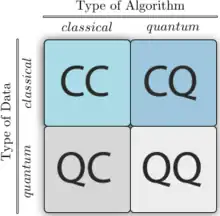
Ya en su nacimiento, el aprendizaje automático cuántico reunió grandes expectativas de proporcionar una solución al análisis de grandes volúmenes de datos utilizando el poder del "paralelismo" de la computación cuántica.[5] Esta tendencia se ha agudizado gracias a las recientes inversiones de empresas como Google y Microsoft en computación cuántica. Sin embargo el aprendizaje automático cuántico está todavía en su etapa inicial y necesita mayores fundamentos teóricos así como resultados científicos sólidos para llegar a ser una disciplina académica. Al igual que su homólogo clásico, el aprendizaje automático cuántico incluye técnicas de aprendizaje supervisado cuántico, aprendizaje no supervisado cuántico y aprendizaje por refuerzo cuántico.[6]
Métodos cuánticos para el aprendizaje automático
Son una serie de ideas de como adaptar los métodos clásicos de aprendizaje automático a los procesos de computación cuántica.[7]
Máquinas de soporte vectorial cuánticas
Las máquinas de soporte vectorial puede ser implementadas en un ordenador cuántico usando una combinación de algoritmos cuánticos ya conocidos.[8] Con el fin de construir el hiperplano que separa el conjunto de datos para las tareas de clasificación, la ecuación lineal para la formulación dual o de mínimos cuadrados se resuelve utilizando un algoritmo cuántico para resolver ecuaciones lineales.[9] Una tarea importante es construir una matriz de densidad cuyas entradas se corresponden con las de la matriz del núcleo. La extracción de la información del estado final puede hacerse a través del análisis de componentes principales cuántico.[10] La clasificación de una nueva entrada se lleva a cabo a través de un ensayo de intercambio. La máquina de soporte vectorial cuántico se ejecuta en tiempo logarítmico respecto a la dimensión del espacio de características y el número de vectores de entrenamiento, mientras que la solución clásica tiene una dependencia polinómica.[10] Los primeros experimentos en máquinas de soporte vectorial cuánticas ya han sido realizados.[11]
Algoritmos cuánticos de agrupamiento y métodos K-nn
Los algoritmos de aprendizaje cuántico tales como k-means o el método K-vecinos más cercanos están basados en calcular la distancia entre los vectores de características y la selección más próxima (ya sea para identificar el grupo centroide más cercano o los vecinos más cercanos a un determinado vector de características. La implementación de estos métodos, basados en la distancia en un ordenador cuántico significa en primer lugar encontrar una manera de calcular distancias clásicas con algoritmos cuánticos. Una idea frecuente es emplear la superposición de dos funciones de onda cuidadosamente preparadas como media de la distancia entre dos estados cuánticos. La distancia mínima puede ser encontrada mediante el Algoritmo de Grover.[12][13] Los algoritmos de aprendizaje automático basados en la distancia, tales como la agrupación sin supervisión, pueden ser implementados a través de la computación cuántica adiabática la cual mejora a la computación clásica de para el algoritmo de Lloyd a (Donde M es el número de vectores de datos N-dimensional y K es el número de agrupaciones).[14]
Redes neuronales cuánticas.
Las redes neuronales cuánticas fueron inicialmente investigadas desde una perspectiva diferente, el papel de los efectos cuánticos en los circuitos neuronales.[15] Sin embargo, el debate pasó rápidamente hacia un enfoque puramente computacional en versiones cuánticas de redes neuronales artificiales, las cuales juegan un papel importante en el aprendizaje automático. Una serie de ideas sobre modelos de redes neuronales cuánticas se han publicado desde entonces.[16][17][18][19][20] Un enfoque interesante para el aprendizaje automático cuántico es el modelo de memoria asociativa cuántica basado en el algoritmo de Grover.[21] Sin embargo, encontrar un método para entrenar una red neuronal cuántica es todavía una tarea abierta.[22]
Con la llegada de las tecnologías NISQ (Computadores cuánticos ruidosos de escala intermedia) se ha propuesto reemplazar la red neuronal por un circuito cuántico, dicho algoritmo se conoce como Aprendizaje de circuito cuántico (Quantum circuit learning), es un algoritmo híbrido, utiliza procesamiento de computadores clásicos y cuánticos. En una red neuronal, la función es aproximada ajustando el parámetro del peso en cada capa, y el concepto es exactamente el mismo en QCL. Se proporcionan datos de entrada a un circuito cuántico y se ajusta iterativamente los parámetros del circuito para que el circuito optimizado proporcione la salida deseada.[23]
Métodos de aprendizaje automático para información cuántica.
El aprendizaje automático cuántico también puede ser usado para los enfoques que aplican métodos clásicos de aprendizaje automático a los problemas de la teoría de la información cuántica. Por ejemplo, cuando los físicos experimentales tienen que lidiar con información incompleta de una fuente o sistema cuántico, la estadística bayesiana y los conceptos de aprendizaje algorítmico pueden ser fructíferamente aplicados. Esto incluye aproximaciones de aprendizaje automático para la clasificación del estado cuántico[24] el aprendizaje del Hamiltoniano[25] y el aprendizaje de una transformación unitaria.[26][27]
Inversiones empresariales en la investigación del aprendizaje automático cuántico.
No solo el mundo académico sino también las empresas líderes en las tecnologías de la información muestran interés en el potencial del aprendizaje automático cuántico. Google Investigation lanzó su laboratorio cuántico de inteligencia artificial en 2013,[28] el cual es una iniciativa conjunta con la NASA y la asociación de universidades de investigación espacial. Una baza importante es el controvertido debate sobre el ordenador cuántico D-Wave.[29] También Microsoft parece interesado en el tema y Peter Lee anunció que va a aumentar la actividad de las empresas en la computación cuántica.[30]
Referencias
- Maria Schuld, Ilya Sinayiskiy, and Francesco Petruccione (2014) An introduction to quantum machine learning, Contemporary Physics, DOI: 10.1080/00107514.2014.964942 (preprint avaiable at arXiv:1409.3097)
- Wittek, Peter (2014). Quantum Machine Learning: What Quantum Computing Means to Data Mining. Academic Press. ISBN 978-0-12-800953-6.
- see for example, Nathan Wiebe, Ashish Kapoor, and Krysta M. Svorey (2014) Quantum Algorithms for Nearest-Neighbor Methods for Supervised and Unsupervised Learning, arXiv:1401.2142v2
- Seth Lloyd, Masoud Mohseni, and Patrick Rebentrost (2014) Quantum algorithms for supervised and unsupervised machine learning, arXiv:1307.0411v2
- «How Quantum Computers and Machine Learning Will Revolutionize Big Data». WIRED. Consultado el 26 de noviembre de 2014.
- Paparo, Giuseppe Davide; Dunjko, Vedran; Makmal, Adi; Martin-Delgado, Miguel Angel; Briegel, Hans J. (8 de julio de 2014). «Quantum Speedup for Active Learning Agents». Physical Review X 4 (3): 031002. doi:10.1103/PhysRevX.4.031002. Consultado el 25 de febrero de 2022.
- For a review, see Maria Schuld, Ilya Sinayiskiy, and Francesco Petruccione (2014) An introduction to quantum machine learning, Contemporary Physics, DOI: 10.1080/00107514.2014.964942 (upcoming, preprint avaiable at arXiv:1409.3097)
- Patrick Rebentrost, Masoud Mohseni, and Seth Lloyd (2014) Quantum support vector machine for big data classification, Physical Review Letters 113 130501
- Aram W. Harrow, Avinatan Hassidim and Seth Lloyd (2009) Quantum Algorithm for Linear Systems of Equations, Physical Review Letters 103 150502
- Seth Lloyd, Masoud Mohseni, and Patrick Rebentrost (2014) Quantum principal component analysis, Nature Physics 10 pp. 631-633
- Zhaokai Li, Xiaomei Liu, Nanyang Xu,1, and Jiangfeng Du (2014) Experimental Realization of Quantum Artificial Intelligence, arXiv preprint arXiv:1410.1054v1
- C. Duerr and P. Hoyer (1996), A quantum algorithm for finding the minimum, arXiv preprint quantph/ 9607014
- Esma Aïmeur, Gilles Brassard, Sébastien Gambs (2013) Quantum speed-up for unsupervised learning, Machine Learning 90, pp. 261-287
- Seth Lloyd, Masoud Mohseni, and Patrick Rebentrost Quantum algorithms for supervised and unsupervised machine learning, arXiv preprint arXiv:1307.0411v2
- Kak (1995). «Quantum neural computing, Advances in Imaging and Electron Physics 94». Sciencedirect.com. pp. 259-313. Consultado el 26 de noviembre de 2014.
- Menneer, T., Narayanan, A. (1995) Quantum-inspired neural networks. Department of Computer Science, University of Exeter, UK, Technical Report 32
- Altaisky, M.V. (2001) Quantum neural network. ArXiv quant-ph/0107012
- Zak, M., Williams, C.P. (1998) Quantum neural nets. International Journal of Theoretical Physics 37(2), pp. 651–684
- Behrman, E.C., Steck, J.E., Skinner, S.R. (1999) A spatial quantum neural computer. In: International Joint Conference on Neural Networks, IEEE IJCNN’99, Vol. 2, pp. 874–877
- Purushothaman, G., Karayiannis, N.B. (1997) Quantum neural networks (qnns): inherently fuzzy feedforward neural networks. IEEE Trans. Neural Netw. 8(3), pp. 679–693
- Dan Ventura, and Tony Martinez (2000) Quantum associative memory, Information Sciences 124 pp. 273-296
- Maria Schuld, Ilya Sinayskiy, Francesco Petruccione (2014) The quest for a Quantum Neural Network, Quantum Information Processing, DOI 10.1007/s11128-014-0809-8
- Mitarai, K.; Negoro, M.; Kitagawa, M.; Fujii, K. (10 de septiembre de 2018). «Quantum circuit learning». Physical Review A 98 (3): 032309. doi:10.1103/PhysRevA.98.032309. Consultado el 10 de julio de 2022.
- G. Sentıs, J. Calsamiglia, R. Munoz-Tapia, and E. Bagan (2012) Quantum learning without quantum memory, Scientific Reports 2 (708), DOI: 10.1038/srep00708
- Nathan Wiebe, Christopher Granade, Christopher Ferrie, and David Cory (2014) Quantum Hamiltonian learning using imperfect quantum resources, Physical Review A 89, 042314
- Alessandro Bisio, Giulio Chiribella, Giacomo Mauro D’Ariano, Stefano Facchini, and Paolo Perinott (2010) Optimal quantum learning of a unitary transformation, Physical Review A 81, 032324
- Jeongho Bang Junghee Ryu, Seokwon Yoo, Marcin Pawłowski, and Jinhyoung Lee, A strategy for quantum algorithm design assisted by machine learning, New Journal of Physics 16 (2014) 073017
- «Google Quantum A.I. Lab Team - Google+». Plus.google.com. Consultado el 26 de noviembre de 2014.
- «NIPS 2009 Demonstration: Binary Classification using Hardware Implementation of Quantum Annealing» (PDF). Static.googleusercontent.com. Consultado el 26 de noviembre de 2014.
- «Microsoft Leans on Machine Learning and Quantum Computing in New Research Strategy - MIT Technology Review». MIT Technology Review. Archivado desde el original el 4 de enero de 2015. Consultado el 26 de noviembre de 2014.