Axonometría ortogonal
La axonometría ortogonal proporciona un método relativamente simple para dibujar una proyección paralela ortogonal de un objeto a partir de dos vistas diédricas asociadas (generalmente, su planta y su alzado). Utiliza el método de incidencia, en el que la imagen de los ejes de coordenadas puede ser elegida (casi) libremente, determinándose a continuación las orientaciones relativas de la planta y del alzado con el procedimiento que se detalla más adelante. Las ventajas de la axonometría ortogonal son:
- a) Un buen aspecto de la imagen dibujada
- b) Las direcciones de los ejes sobre el plano de dibujo se pueden seleccionar libremente
- c) El contorno de una esfera es una circunferencia
- d) Es un método de incidencia rápido, que no requiere acortar ni aplicar coordenadas individuales: una vez orientados la planta y el alzado del modelo, para determinar la posición de un punto en el dibujo axonométrico basta con dibujar rectas paralelas a las direcciones de incidencia y cortar los rayos asociados.
Descripción del método
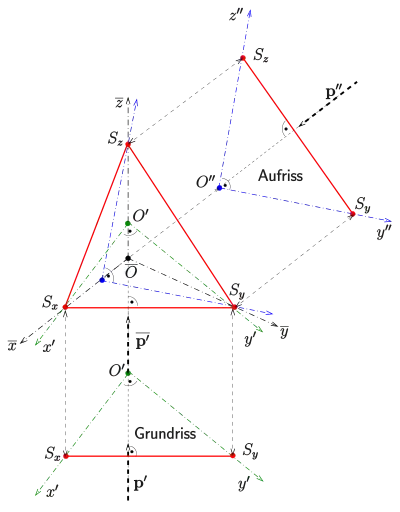
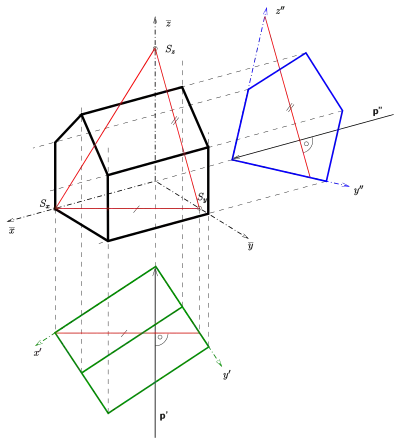
Dado un sistema de coordenadas tridimensionales xyz, el método se basa en elegir arbitrariamente la proyección de los tres ejes de coordenadas sobre el plano de dibujo (direcciones ), y a partir de estos tres ejes, determinar la orientación relativa de la vista en planta (proyección sobre el plano xy) y de la vista en alzado (proyección sobre el plano yz) de un objeto, que van a facilitar su representación axonométrica ortogonal mediante el procedimiento de incidencia de rayos. La dirección de proyección resultante, es la normal al plano representado por el triángulo de referencia , intersección del citado plano perpendicular a la dirección de proyección, con los tres planos de coordenadas:
- Selecciónense las direcciones de los 3 ejes de coordenadas (no todos colineales) en el plano del dibujo ().
- Elegido un punto cualquiera (como ) construir el triángulo , teniendo en cuenta que sus lados son perpendiculares a los ejes de coordenadas opuestos ( a ; a ; y finalmente a ). Lógicamente, la imagen del origen de coordenadas es el punto de intersección de las alturas del triángulo .
- Determinar el punto , abatimiento de sobre el plano horizontal. Para ello, se utiliza la propiedad de que el ángulo tiene 90° y que debe quedar proyectado sobre el eje . Para ello, basta determinar la intersección de la circunferencia con centro en el punto medio del segmento por un lado y el eje por otro. El ángulo determina la orientación del plano de planta.
- Determinar el punto , abatimiento de sobre el plano del alzado. Para ello, se utiliza la propiedad de que el ángulo tiene 90° y que debe quedar proyectado sobre el eje . Para ello, basta determinar la intersección de la circunferencia con centro en el punto medio del segmento por un lado y el eje por otro. El ángulo determina la orientación del plano del alzado.
- Una vez localizadas las orientaciones relativas de la planta y del alzado, se puede iniciar el dibujo de la perspectiva axonométrica ortonormal por el procedimiento de incidencia.
Justificación del procedimiento
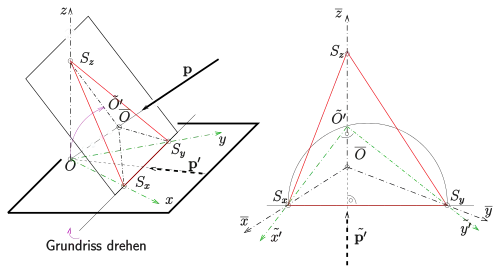
Una proyección paralela ortogonal queda unívocamente determinada especificando la dirección de proyección . El plano del dibujo es perpendicular a la dirección de proyección y se puede deslizar a lo largo de la dirección de proyección como se desee sin alterar el resultado del dibujo. Para obtener una imagen vívida del objeto espacial, se debe elegir una dirección de proyección que no sea paralela ninguno de los tres ejes de coordenadas. Por lo tanto, los tres ejes de coordenadas intersecan el plano del dibujo en los puntos de referencia . Con la elección de un punto de referencia, los otros dos quedan fijados automáticamente. Las imágenes de los ejes de coordenadas son las alturas del triángulo formado por estos tres puntos, y la imagen del origen de coordenadas es la intersección de estas alturas. Cuando el plano de planta (plano xy) se abate alrededor de la línea recta , la imagen del punto cero se desplaza sobre el eje al punto . Los puntos de referencia permanecen sin cambios durante el proceso de giro. Así que la línea a través de es el eje x abatido desde el plano de dibujo. De manera similar, se obtiene el eje y abatido, y por lo tanto, el plano de planta sin distorsión (plano xy). Para no alterar la imagen axonométrica, se debe dibujar el plano de planta orientándolo en la dirección del eje hacia abajo. El procedimiento es análogo para el alzado (plano yz). Las dos direcciones principales del proceso de incisión resultante son las direcciones del eje y del eje .
Esfera y circunferencia

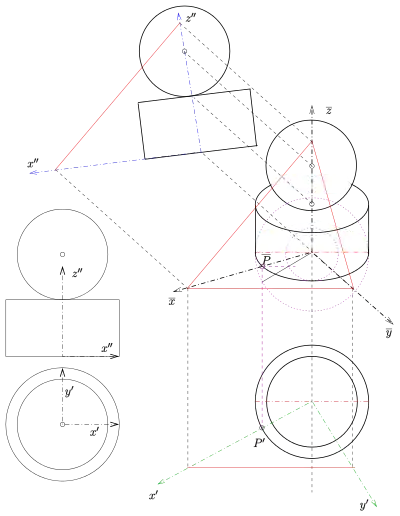
Las esferas son particularmente fáciles de visualizar en la axonometría ortogonal: el contorno de una esfera es una circunferencia con el radio de la esfera. Para obtener una imagen de una esfera, basta con determinar la imagen de su centro y luego se debe dibujar la circunferencia de su contorno. En una proyección paralela oblicua, el contorno de una esfera es siempre una elipse, cuyos ejes principales deben determinarse laboriosamente.
La proyección ortogonal de una circunferencia cuando está en un plano paralelo al del dibujo es otra circunferencia sin distorsión. En cualquier otro caso, aparece como una elipse, cuyo centro es la imagen del centro de la circunferencia. Las direcciones de los ejes principales y el tamaño de los semiejes se pueden determinar mediante la construcción de Rytz.
En una proyección paralela ortogonal, el diámetro de una circunferencia situada en un plano paralelo a algún plano de coordenadas, aparece sin distorsión en el eje mayor de la elipse que forma su imagen. El punto central, la dirección del semieje mayor y su longitud (= radio del círculo) se determinan automáticamente en la proyección axonométrica. El tamaño del semieje menor se determina de acuerdo con el diagrama adjunto, a partir del conocimiento del eje mayor y de un punto de la elipse. En el ejemplo, los círculos inferior y superior de un cilindro son paralelos al plano xy. Las líneas rectas del plano xy, que son paralelas a la planta del dibujo, son todas paralelas a la línea recta . Por lo tanto, el diámetro del círculo inferior que es paralelo a esta recta, se muestra sin distorsión. Como conocido el semieje mayor, basta un punto de la elipse basta para realizar la construcción que permite determinar su semieje menor, aquí se ha utilizado el punto de la circunferencia en el eje x. La imagen del círculo superior del cilindro es la imagen del círculo inferior desplazada hacia arriba.
Definiciones alternativas
En lugar de partir como se ha hecho anteriormente de las imágenes de los ejes, también se puede definir una axonometría ortogonal por los procedimientos siguientes:
- Especificando el triángulo de puntos de referencia: el dibujo de los ejes coordenados coincide con las alturas de este triángulo, y el origen del sistema de coordenadas es la intersección de las tres alturas.
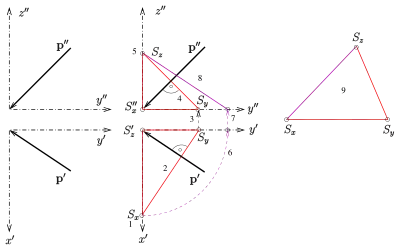
- Especificando la dirección de proyección en planta y alzado (véase la imagen adjunta): para construir el triángulo de referencia, basta con elegir un punto cualquiera como del eje x. Dado que la recta debe ser perpendicular a , extendiéndola se determina el punto , dado por la intersección de la perpendicular a desde con el eje y en planta. Con un razonamiento análogo, se determina en el alzado (véase la imagen). Las longitudes de los lados y se pueden reconocer en la planta o en el alzado. La longitud de resulta de la 'rotación paralela' al plano del alzado (véase longitud verdadera). Por lo tanto, es posible dibujar el triángulo de referencia porque se conocen las longitudes todos sus lados (los números en el dibujo indican el orden de los pasos de construcción).
Procedimiento inverso
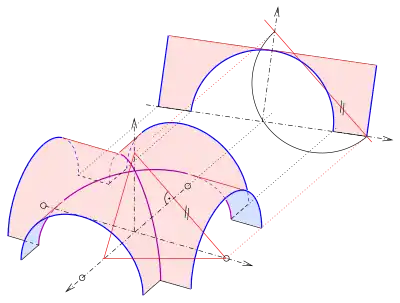
Suponiendo que una imagen es una proyección paralela ortogonal en la que se pueden identificar las imágenes de los ejes, entonces es posible invertir las construcciones anteriores para determinar la planta y el alzado originales de la imagen. La dirección de proyección también se puede determinar en la reconstrucción.
Ejemplo: determinación de un alzado
Dada la Axonometría ortogonal de una bóveda de crucería Se busca: determinar las dimensiones reales de su alzado.
Solución:
|
Bibliografía
- Fucke, Kirch, Nickel: Darstellende Geometrie. Fachbuch-Verlag, Leipzig 1998, ISBN 3-446-00778-4
- Cornelie Leopold: Geometrische Grundlagen der Architekturdarstellung. Verlag W. Kohlhammer, Stuttgart 2005, ISBN 3-17-018489-X
Enlaces externos
- Normale (orthogonale) Axonometrie mit einfachen Beispielen
- Darstellende Geometrie für Architekten (PDF; 1,5 MB). Skript (Uni Darmstadt), S. 42