Búsqueda de patrones (optimización)
La búsqueda de patrones (conocida también como búsqueda directa, búsqueda sin derivados o búsqueda de caja negra) es una familia de métodos de optimización numérica que no requiere un gradiente. Como resultado, se puede usar en funciones que no son continuas o diferenciables. Uno de estos métodos de búsqueda de patrones es la «convergencia», que se basa en la teoría de las bases positivas. La optimización intenta encontrar la mejor coincidencia (la solución que tiene el valor de error más bajo) en un espacio de posibilidades del análisis multidimensional.
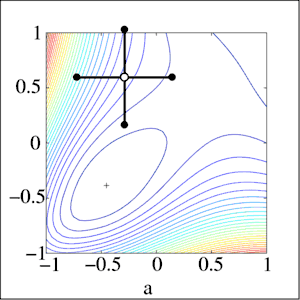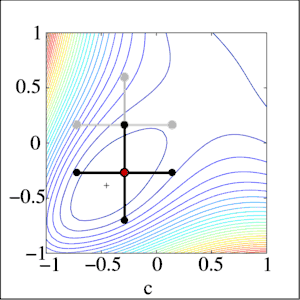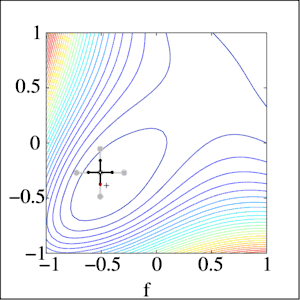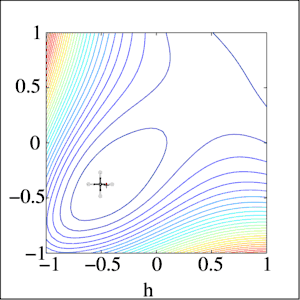
Historia
El nombre de «búsqueda de patrones» fue acuñado por Hooke y Jeeves.[1] Una variante temprana y sencilla se atribuye a Fermi y Metropolis cuando trabajaban en el Laboratorio Nacional de Los Álamos. Es descrito por Davidon,[2] de la siguiente manera:
Variaron un parámetro teórico al mismo tiempo, por pasos de la misma magnitud y cuando ningún parámetro aumentó ni disminuyó, mejoraron aún más el ajuste a los datos experimentales, redujeron a la mitad el tamaño del paso y repitieron el proceso hasta que los pasos se consideraron suficientemente pequeños.
Convergencia
La convergencia es un método de búsqueda de patrones propuesto por Yu, quien demostró que converge utilizando la teoría de las bases positivas.[3] Más tarde, Torczon, Lagarias et al.[4][5] utilizaron técnicas de base positiva para demostrar la convergencia de otro método de búsqueda de patrones en clases de funciones específicas. Fuera de tales clases, la búsqueda de patrones es una heurística que puede proporcionar soluciones aproximadas útiles para algunos problemas, pero puede fallar en otros. La búsqueda de patrones no es un método iterativo que converge en una solución; de hecho, los métodos de búsqueda de patrones pueden converger en puntos no estacionarios en algunos problemas relativamente sencillos.[6][7]
Véase también
- Búsqueda de sección áurea conceptualmente se asemeja a la búsqueda de patrones en la reducción del rango de búsqueda, solo para espacios unidimensionales.
- Método Nelder-Mead también conocido como método símplex se parece conceptualmente a la búsqueda de patrones en la reducción del rango de búsqueda para espacios de búsqueda multidimensionales, pero lo hace manteniendo n + 1 puntos para espacios n-dimensionales, mientras que los métodos de búsqueda de patrones calculan 2n + 1 puntos (el punto central y 2 puntos en cada dimensión).
- Luus–Jaakola toma muestras de una distribución uniforme que rodea la posición actual y usa una fórmula simple para disminuir exponencialmente el rango de muestreo.
- Búsqueda aleatoria es una familia de métodos de optimización que toman muestras de una hiperesfera que rodea la posición actual.
- Optimización aleatoria es una familia de métodos de optimización que muestrean una distribución normal que rodea la posición actual.
Referencias
- Hooke, Robert; Jeeves, T. A. (1961). «"Direct Search" Solution of Numerical and Statistical Problems». Journal of the ACM 8 (2): 212-229. ISSN 0004-5411. doi:10.1145/321062.321069.
- Davidon, William C. (1991). «Variable Metric Method for Minimization». SIAM Journal on Optimization 1 (1): 1-17. ISSN 1052-6234. doi:10.1137/0801001.
- Yu, Wen Ci. 1979. “Positive basis and a class of direct search techniques”. Scientia Sinica [Zhongguo Kexue]: 53—68.
- Torczon, Virginia (1997). «On the Convergence of Pattern Search Algorithms». SIAM Journal on Optimization 7 (1): 1-25. ISSN 1052-6234. doi:10.1137/S1052623493250780.
- Dolan, Elizabeth D.; Lewis, Robert Michael; Torczon, Virginia (2003). «On the Local Convergence of Pattern Search». SIAM Journal on Optimization 14 (2): 567-583. ISSN 1052-6234. doi:10.1137/S1052623400374495.
- Powell, M. J. D. (1973). «On search directions for minimization algorithms». Mathematical Programming (en inglés) 4 (1): 193-201. ISSN 1436-4646. doi:10.1007/BF01584660.
- McKinnon, K. I. M. (1999). «Convergence of the Nelder–Mead simplex method to a non-stationary point». SIAM J. Optim. 9: 148-158. doi:10.1137/S1052623496303482."Convergence of the Nelder–Mead simplex method to a non-stationary point". SIAM J. Optim. 9: 148–158. CiteSeerX 10.1.1.52.3900. doi:10.1137/S1052623496303482. (algorithm summary online).
Enlaces externos
- Esta obra contiene una traducción derivada de «Pattern search (optimization)» de Wikipedia en inglés, concretamente de esta versión del 19 de febrero de 2021, publicada por sus editores bajo la Licencia de documentación libre de GNU y la Licencia Creative Commons Atribución-CompartirIgual 4.0 Internacional.