Cálculo de engranajes
Un engranaje es un elemento destinado a transmitir el movimiento sin deslizar, para ello los engranajes presentan una superficie dentada, destinada a engranar uno con otro, de modo que ese movimiento sea posible, realizando una transmisión del desplazamiento exacta. Además de utilizarlo para transmisión de movimiento circular - circular entre piñones, puede dedicarse a conversor de movimiento circular - lineal y viceversa, por medio del mecanismo piñón cremallera.
Partes de un engranaje


En un engranaje se diferencia:
- Corona: Que es la parte exterior, donde están tallados los dientes.
- Cubo: la parte central del engranaje, por el que se fija al eje.
Aquí se tratará únicamente las dimensiones de la corona.
Dimensiones fundamentales
La circunferencia que definiría la superficie por la cual el engranaje rueda sin deslizar la llamaremos circunferencia primitiva.
El diámetro primitivo (d) Se considera una circunferencia equivalente al contacto que tendría si se tratara de una rueda de fricción (Rueda sin dientes), el diámetro primitivo queda situado a media altura de los dientes.
El número de dientes (z), es el número total de dientes de la corona del engranaje en toda su circunferencia.
El paso (p) es el arco de circunferencia, sobre la circunferencia primitiva, entre los centros de los dientes consecutivos.
Entonces la longitud de la circunferencia primitiva es:
Luego:
Esto es:
El módulo (m) de un engranaje es la relación que existe entre el diámetro primitivo y el número de dientes, que es el mismo que la relación entre el paso y
El módulo es una magnitud de longitud, expresada en milímetros, para que dos engranajes puedan engranar tienen que tener el mismo módulo, el módulo podría tomar un valor cualquiera, pero en la práctica está normalizado según el siguiente criterio:
- De 1 a 4 en incrementos de 0,25 mm
- De 4 a 7 en incrementos de 0,50 mm
- De 7 a 14 en incrementos de 1 mm
- De 14 a 20 en incrementos de 2 mm
Dimensiones del engranaje

- Circunferencia exterior: es la circunferencia que pasa por la parte exterior de las cabezas de los dientes.
- Diámetro exterior (de): es el que corresponde a la circunferencia exterior.
- Circunferencia interior: es la que pasa por la base de los pies de los dientes.
- Diámetro interior (di): es el que corresponde a la circunferencia interior.
- Cabeza de diente (hc): es la parte del diente comprendida entre la circunferencia primitiva y la circunferencia exterior. Toma el valor del módulo: hc= m
- Pie de diente (hp): es la parte del diente comprendida entre la circunferencia interior y la primitiva. Toma el valor de 1,25 veces el módulo: hp= 1,25m
- Altura del diente (h): es la distancia entre la circunferencia interior y la exterior. Por tanto tiene el valor de 2,25 veces el módulo: h= 2,25m
- Longitud del diente (b): es la anchura de la corona, sobre la que se tallan los dientes, en general suele tener un valor de 10 veces el módulo: b= 10m
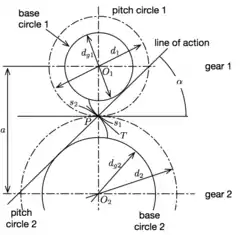
Forma de involuta en dientes de engranaje
La involuta es una curva que se genera al desenrollar una cuerda tirante de un cilindro (llamado evoluta).
Para cumplir con la ley fundamental de engranaje, los contornos de los dientes deben de conjugarse entre sí. Existe un gran número de pares conjugados que se pueden utilizar, pero se usa en mayor medida la forma de involuta debido a que las normales comunes de los puntos de contacto de los dientes pasan por el mismo punto de paso.
Diámetro Pitch (Pt)
En el sistema inglés de unidades, con la pulgada como unidad de longitud, el cálculo de engranajes emplea el denominado diámetro Pitch.
Para un engranaje dado, el diámetro Pitch (Pt) es igual al número de dientes por pulgada en el diámetro primitivo. La relación entre el diámetro Pitch y el módulo es;
Dibujar un engranaje
Hey describe un procedimiento de representación gráfica de engranajes rectos.
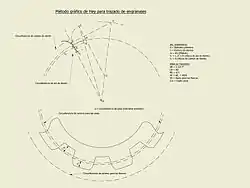
Sobre la circunferencia primitiva de diámetro se traza un radio. Partiendo del punto de intersección con la circunferencia primitiva , se traza una perpendicular al radio de longitud para obtener , siendo el paso circular. Se traza una paralela al radio desde . Se traslada la magnitud sobre la paralela, hallando . es el resultado de medir desde . Este punto se une con , prolongando la recta.
Sobre y partiendo de , se marcan a ambos lados los puntos y , ambos a una distancia , trazando por estos puntos paralelas a hasta interseccionar la prolongación de y el radio en los puntos y respectivamente. Por último, se encuentra el simétrico de en la prolongación de .
servirá de centro para trazar las caras de los dientes con radio , en tanto que lo será para trazar los flancos con radio .